Poisson分布(ポアソン分布)は以下のような確率分布をもつ。
![]()
![]() は平均値である。また、Poisson分布の平均値と分散は
は平均値である。また、Poisson分布の平均値と分散は
![]()
である。平均も分散も ![]() になる。
になる。
このPoisson分布の平均値の意味やら導出やらをまとめておく。
目次
1. Poisson分布
簡単に概要を書いておく。
Poisson分布について
![]() は平均値と書いたが、その意味はたくさんの試行を繰り返した場合にある事象が起こる回数の平均のことである。
は平均値と書いたが、その意味はたくさんの試行を繰り返した場合にある事象が起こる回数の平均のことである。
よくあるのが不良品の例はわかりやすい。おそらくPoisson分布の基本的な問題には
「1000回に10個の不良品を出す機械」
のようなフレーズが含まれるだろう。これは平均が10/1000となるように機械が不良品を出すという意味である。 10000回製品を作るならば平均して100個の不良品を出す。
Poisson分布の使い方:基本例題
問題例:
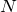 =1000回に30個の不良品
=1000回に30個の不良品- 100個の製品を調べる
- そのうち不良品が5個ある確率を求める
Poisson分布:
![]()
である。1より機械がつくる100個の製品のうち3個が不良品となる。したがって、100個のうちの不良品の数の平均もまた ![]() である。3は「
である。3は「 ![]() に対応する
に対応する ![]() を求めよ」の意味である。上の
を求めよ」の意味である。上の ![]() に
に ![]() を代入すれば良い。
を代入すれば良い。
2. Poisson分布の平均値・分散など導出
ここでは、平均と分散は![]() で計算していく。母関数は使わない。分布の導出には母関数を使う。
で計算していく。母関数は使わない。分布の導出には母関数を使う。
平均値の計算
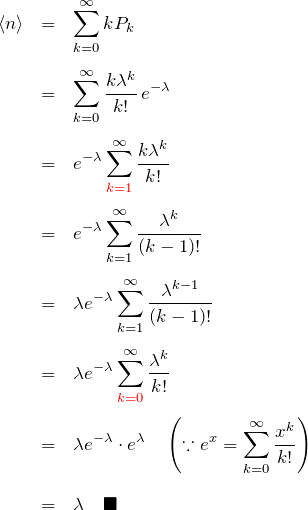
![]() の取り方などに注意する。2行目の
の取り方などに注意する。2行目の ![]() の中身は
の中身は ![]() のとき 0 であるため、実質
のとき 0 であるため、実質 ![]() からの和である。したがって、3行目では
からの和である。したがって、3行目では ![]() からの
からの ![]() になる。また、6行目では
になる。また、6行目では ![]() から始めると
から始めると ![]() なので、
なので、![]() にして
にして ![]() から始めている。
から始めている。
以下で見るように、Poisson分布は平均値を ![]() で一定にしているので、得られた結果
で一定にしているので、得られた結果 ![]() は当たり前である。
は当たり前である。
分散の計算
分散は、平均値からの差の2乗の平均である。
![]()
![]() は上で計算した通りである。したがって、
は上で計算した通りである。したがって、![]() を計算すれば良い。
を計算すれば良い。
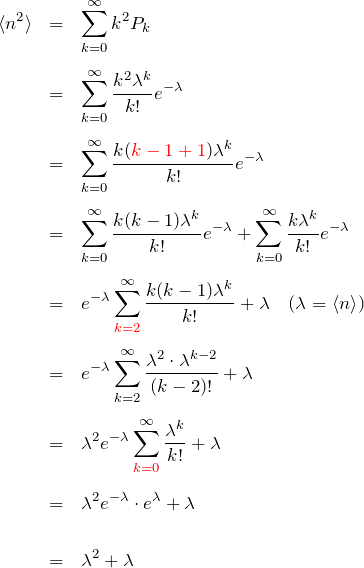
したがって分散は
![]()
Poisson分布では分散も ![]() になる。
になる。
Poisson分布を導出する前に
はじめに落とし穴を説明しておく。
ある確率 ![]() で不良品を出す機械があるとしよう。この機械が
で不良品を出す機械があるとしよう。この機械が ![]() 個の製品を出したときに、不良品の数
個の製品を出したときに、不良品の数 ![]() の期待値を
の期待値を ![]() とする。 つまり、
とする。 つまり、
![]()
としておく。Poisson 分布では ![]() 、すなわち、不良品の数
、すなわち、不良品の数 ![]() の平均値が一定であるとする。
の平均値が一定であるとする。
よって、![]() であれば
であれば
- 100個のうち不良品の数の平均は 1 個
- 1000個のうち不良品の数の平均は 10 個
- 100000個のうち不良品の数の平均は 1000 個
である。
何をあたりまえのことを…と思うだろう。しかし、不思議なのはその機械が毎回 確率 ![]() で不良品を出していることである。
で不良品を出していることである。
「毎回 ![]() で不良品、
で不良品、![]() で不良品でない」という確率は二項分布である。
で不良品でない」という確率は二項分布である。
したがって、![]() 回の試行のうち、不良品の数が
回の試行のうち、不良品の数が ![]() である確率は
である確率は
![]()
である。二項分布のときの ![]() の期待値は、(試行回数
の期待値は、(試行回数![]() )×(事象が起こる確率
)×(事象が起こる確率![]() )であった。つまり、
)であった。つまり、
![]()
となる。いまPoisson分布においては、![]() の定数であった。
の定数であった。
すると上の ![]() とどんどん増やしていった例では、
とどんどん増やしていった例では、![]() はどんどん小さくなっていく。 これを
はどんどん小さくなっていく。 これを ![]() を増やせば
を増やせば ![]() が減る、すなわち、「機械は不良品をどんどん出しにくくなる」と考えるのは無意味である。
が減る、すなわち、「機械は不良品をどんどん出しにくくなる」と考えるのは無意味である。
直感的には理解しにくいが、
Poisson分布は ![]() の平均値
の平均値 ![]() を固定した分布である。
を固定した分布である。
したがって、1000回のときの平均値が0.1であれば、100回の時の平均値もまた0.1である。以下のPoisson分布の導出では、![]() を考える。
を考える。
*二項分布との違い:二項分布はコインを ![]() 回投げた場合、表が
回投げた場合、表が ![]() 回出る確率
回出る確率 ![]() などの分布を表す。何回投げても「1回の事象でコインが表になる確率
などの分布を表す。何回投げても「1回の事象でコインが表になる確率 ![]() 」は変わるはずがない。ここで変わるのは、表が出る回数
」は変わるはずがない。ここで変わるのは、表が出る回数 ![]() の平均値
の平均値 ![]() である。直感的に100回投げたら表が出る回数は50回に近いだろうし、1000回投げたら500回に近い。この場合、
である。直感的に100回投げたら表が出る回数は50回に近いだろうし、1000回投げたら500回に近い。この場合、![]() と
と ![]() になる。 したがって、試行回数を増やせば
になる。 したがって、試行回数を増やせば ![]() の平均値は変わる。
の平均値は変わる。
Poisson分布の導出
機械は一回の事象で ![]() の確率で不良品を出すとすると、
の確率で不良品を出すとすると、![]() 回の試行で不良品が
回の試行で不良品が ![]() 回出る確率は
回出る確率は
![]()
これは二項分布であり、![]() の平均値は
の平均値は
![]()
である。
![]() を固定して、
を固定して、![]() を考えよう。
母関数
を考えよう。
母関数
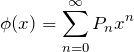
を用意して導出する。
母関数を計算しておこう。
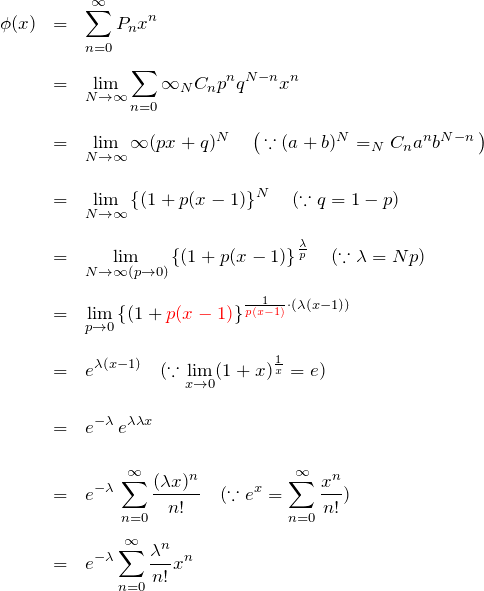
となる。
最後の結果と1行目を改めて書いておく。
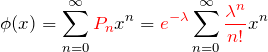
![]() の係数を比較して
の係数を比較して
![]()
を得る。
* これは Poissonの極限定理(wikipedia)である。
3. まとめ
Poisson分布について説明してきた。Poisson分布の平均値と分散は ![]() で計算してきた。これには最後のところで得た母関数を用いた計算方法もある。
で計算してきた。これには最後のところで得た母関数を用いた計算方法もある。