フーリエ変換を解説していきましょう。ここではフーリエ変換がどんなものか知ってもらうため、数式を使わないことにした。したがって、フーリエ変換の定義すらしない。
1. フーリエ変換のイメージ(基本編)
1.1 わかりやすい例(聖徳太子さん)
聖徳太子(厩戸王)さんは10人の話を理解できたらしい。ここでは下の図のような3人が言葉を同時に発している場合を考える。
文字の大きさは声の大きさを表している。
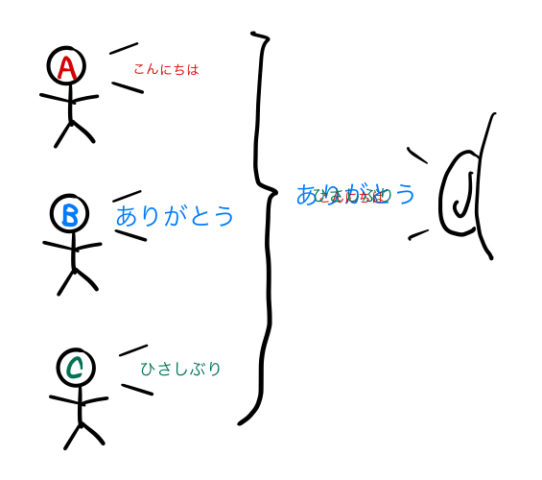
聖徳太子さんはそれぞれ、「こんにちは」「ありがとう」「ひさしぶり」を同時に聞くことになる。
彼なら聞こえてきた「ごちゃ混ぜの音」も
「どの言葉(だれ)」が「どのくらいの声の大きさ」で
話しているかがわかるだろう。つまり、下の図のように分解できる。
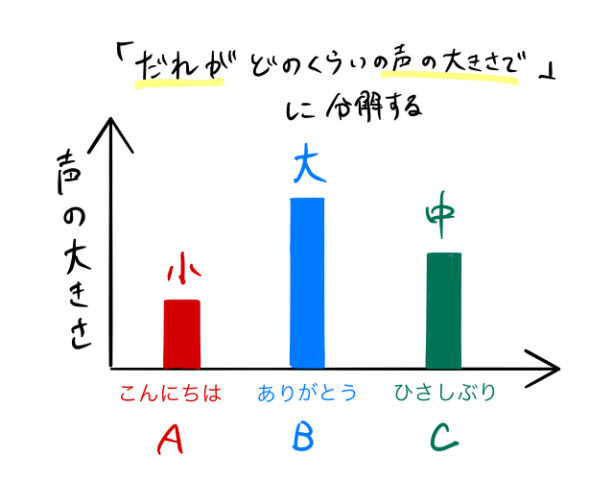
このような、「さまざまな要素が混ざり合っているもの」を「それぞれの要素」に分解するのがフーリエ変換のイメージである。このとき、分解した結果として、
- 要素が何か(横軸)
- 要素はどれくらいの重みがあるか(縦軸)
が重要になる。
1.2 波の分解
先ほどは要素として「こんにちは」「ありがとう」「ひさしぶり」を考えたが、ここではより一般的な波を考えることにする。
やることは先ほどと変わらない。それぞれの言葉を波に置き換えた。
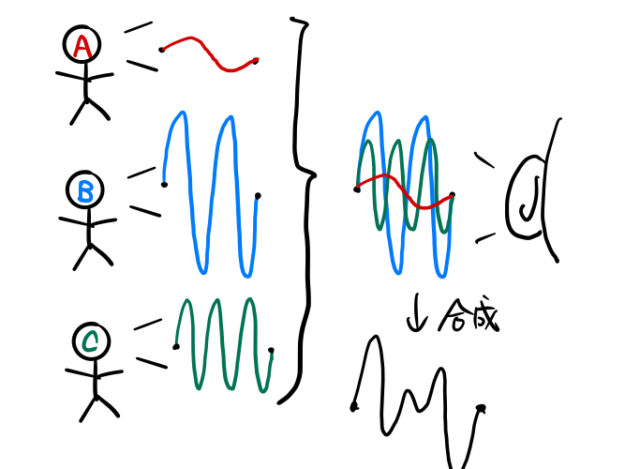
- 言葉
 波
波 - 言葉の種類
 波の山の数
波の山の数 - 声の大きさ
 波の山の高さ(振幅)
波の山の高さ(振幅)
それぞれの3つの波を合成した波を作ることもできる。上の絵には合成した波を描いた。
波を「山の数」と「山の高さ」でまとめると下のようになる。山の高さはわかりやすいように小さい方から 1、2、3 とした。
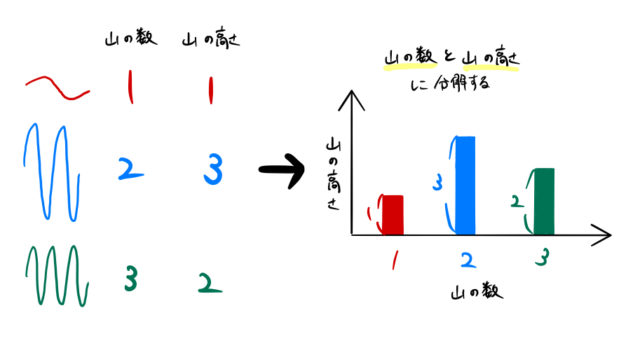
この数字を、横軸に「山の数」、縦軸に「山の高さ」として表すことができる。これでフーリエ変換は完了したことになる。
実際は「合成された後の波」から出発して、その合成波がどのような波でできているか調べるのがフーリエ解析である。これは合成波をそれぞれの波に「分解」する感じである。
一方で、それぞれの波から合成波をつくる変換が「逆フーリエ変換」に対応するイメージである。したがって、下のような関係にある。
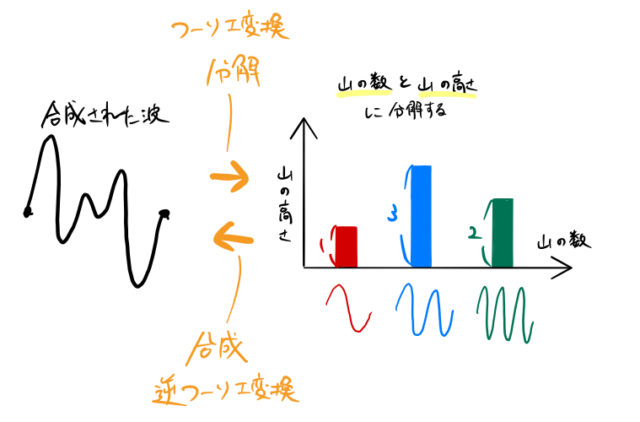
波の「分解」と「合成」がフーリエ解析の重要なポイントである。
2. フーリエ変換でノイズを除く(応用編)
ちょっとだけフーリエ変換の応用について書きます。
フーリエ変換は合成波をそれぞれの波の要素に分解できた。もしかしたら、ノイズのようにいらない波の要素も入っているかもしない。
たとえば、聖徳太子に向かって3人が「こんにちは」「ありがとう」「ひさしぶり」とパーティー会場で言った場合はノイズだらけになるだろう。
画像でも音でも、波の中にあるノイズを取り除くことができるのがフーリエ変換の応用になる。
ノイズを取り除くイメージは下の絵ようになる。左上から時計回りに進む。
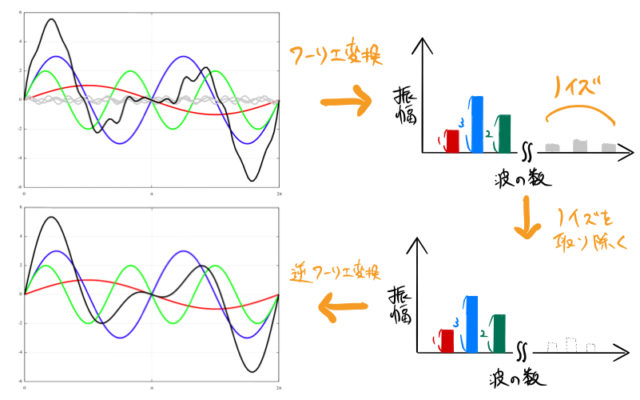
ノイズを取り除くイメージ:
- 左上:合成波(黒線)は赤、青、緑の波 以外のノイズを含む
- 右上:合成波をフーリエ変換すると、ノイズ成分が抽出できる
- 右下:ノイズ成分を取り除く、つまり、振幅を0にする
- 左下:逆フーリエ変換によって綺麗な合成波(黒線)を得る
このように、元の波から不要な波の要素を取り除いた波を再構築することができる。
ここでは不要な波としてノイズを考えた。他にも特定の波の成分を取り除くことができるため、画像データ、音楽データ、動画データなどの圧縮にも使われる。
音楽の場合は、高音すぎる音(振動数の大きい波)の成分は人間が聞き取ることができないため、取り除いても音質は変わらないだろう。画像や動画データについても同じく、いらない成分をフーリエ解析によって取り除くことができるだろう。
このように不要な成分を取り除くため、以下のような特徴がある。
- データの容量が減る
- 音質・画質などが落ちる
圧縮されたファイル形式として、MP3形式やMPEG形式などが挙げられる。
イメージだけ伝われば良いため、ここではこれ以上立ち入らない。
3. まとめ
例を使ってフーリエ解析のイメージを伝えてきた。
- フーリエ変換のイメージ
- フーリエ解析を使ったノイズ除去
の話をメインに進めた。しかし、フーリエ変換の導入部であるため、
- フーリエ変換の定義
- どのようにフーリエ変換するか
- 時間
 周波数 などの対応関係
周波数 などの対応関係
については触れなかった。これを扱うためには数式の導入が必要になるが、これは違うところで説明する。