【重積分】面積のイメージで学ぶ「ヤコビアン」の意味

　ここではヤコビアンのイメージを伝えるため、 2変数関数の重積分（面積）を例にとる。 平面→ 平面の変数変換によるヤコビアン(ヤコビ行列; Jacobian matrix)は

   

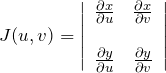
である。

1. ヤコビアンのイメージ

平面の中にある図形の面積を求めるために工夫をする。 その過程でヤコビアンが必要になる。そのことを順に見ていこう。

xy平面の面積

　下の赤い線で囲まれた図形の面積を求めたい。 平面で積分しようとすると少し計算が煩雑である。

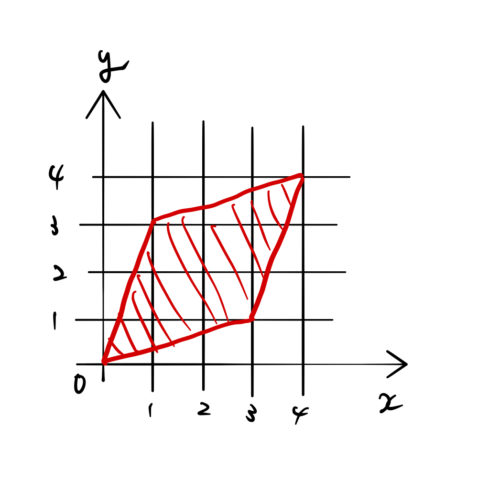
ここでは、

「積分して面積を求めること」

を

「面積１の正方形タイル何個分であるか求めること」

と考えて説明していく。簡単な例なのでタイルの数はすぐに求められるが、タイルの数（面積）を変数変換によって求めていく。

なぜ変数変換するのか

　数学でも物理でも、変数変換は頻出である。変数変換する理由は、

• 式の形をかんたんにする
• 式の形を計算をかんたんにする

などいろいろな理由がある。ここでは積分計算を簡単にするための変数変換について主に扱う。

　上の赤い線で囲まれた面積を求めるために、 を変数変換して にしたとする。 この変数変換により、下図のように座標系の軸が変わるものを選ぶ。

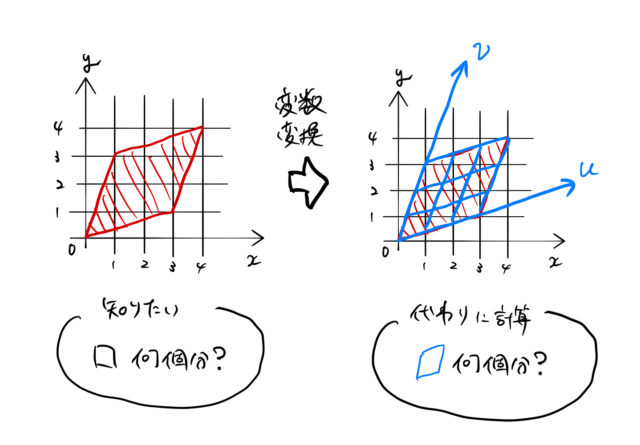
このような軸をもつ 平面に変数変換できれば、

「 平面で面積１の正方形タイルは何個？」

という問題を

「 平面で面積~~~のタイルは何個？」

という問題に変えることができる。

　見ての通り、新しい 平面で用意したタイルで赤い図形を埋めるのは簡単そうである。 たとえば、上のような青いタイルを９個分使えばよいことがわかる。

uv平面のタイル

　ここで、ひとつの問題がある。

「 平面で用意するタイルの大きさがいろいろある」

ということである。 下図のように大きさの異なるタイルを用意すれば、同じ図形でも必要となるタイルの数は異なる。 図の左の大きなタイルを用いると４個で済むし、右の小さなタイルを用いると２５個いる。

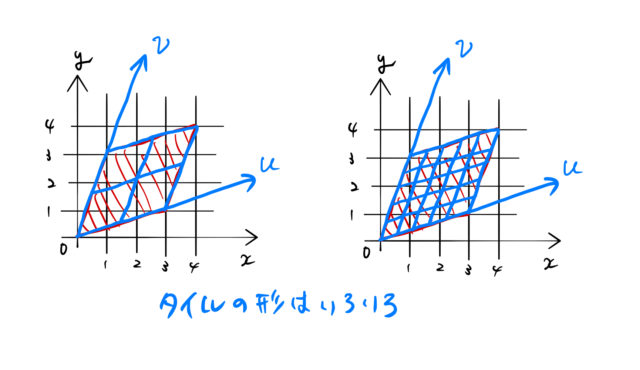
　用意したタイルの大きさによって、同じ図形の面積がいろいろな値をとるのはおかしい。 そこで、 平面で用意したタイルが、元の 平面での正方形タイル（面積１）と比べてどのくらい大きいかを考慮すれば良いことがわかる。

　その役割をするのがヤコビアンである。もう少し正確な表現を見ていく。

ヤコビアンの意味

　同じ図形を 平面と、変数変換した先の 平面で測る。このとき、それぞれの平面で「基準となるタイル」の大きさが同じとは限らない。

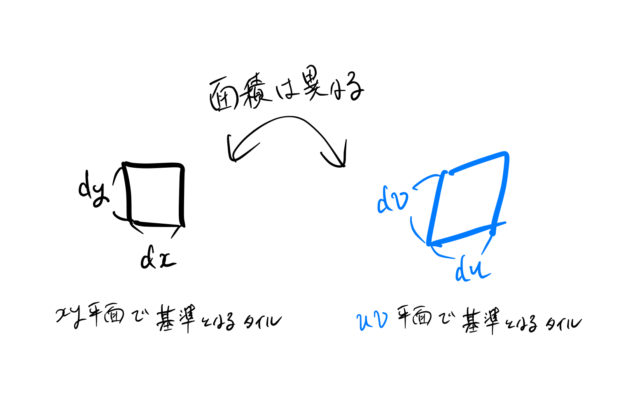
　すなわち、基準となる と の面積は異なる。

　知りたい面積は で測られたもの（タイル何個分か）であり、 で測られたものではない。最も単純な変換として面積を と で測る例など考えられる。

　ヤコビアン は に変換するための 倍のような役割をする。つまり、 の変換のために 倍するのである。

　注意点として、一般の は で の関数であって、定数ではない。つまり、用意するタイル と の比は位置 によって異なる。表式として

   

と書く。

重積分の中にあるときは

   

となる。

二次元極座標変換の絵

　二次元極座標変換

   

についてヤコビアンを計算すると

   

である。

したがって、

   

となる。「基準となるタイル」が に依存するのは以下の絵からわかる。

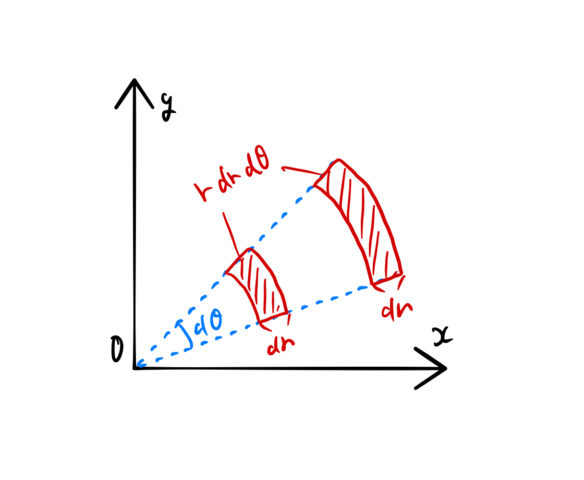
原点から離れるほど、 は大きくなる。

2. まとめ

　面積を例にとってヤコビアンの意味を見てきた。体積に関する話でも、４次元以上でも同じように考えることができる。

　 平面において、もっとグニャグニャの図形でも、うまい変数変換により簡単に面積が求められることもある。