3次元の自由電子の状態密度は、![]() に比例する。
に比例する。
自由電子でない場合の一般的な場合、3次元の状態密度は
![]()
である。![]() は
は ![]() 番目のバンドを表す。係数の2は電子のスピンの自由度、
番目のバンドを表す。係数の2は電子のスピンの自由度、![]() はセルの体積を表す。
はセルの体積を表す。![]() は
は ![]() についての勾配をとることを表し、この式の
についての勾配をとることを表し、この式の ![]() は第一ブリルアンゾーン内の
は第一ブリルアンゾーン内の ![]() 点を表す。
点を表す。
この式を導出して、![]() など勾配(gradient)の話を簡単にまとめておく。
など勾配(gradient)の話を簡単にまとめておく。
1. 自由電子との違い
エネルギーと波数k
自由電子の場合のエネルギーの ![]() の関係は
の関係は
![]()
であった。したがって、![]() のそこそこ大きいところで、等エネルギー面は球面になった。 このことは、フェルミ波数
のそこそこ大きいところで、等エネルギー面は球面になった。 このことは、フェルミ波数 ![]() まで詰まったエネルギー面が フェルミ球 になることからわかる。
まで詰まったエネルギー面が フェルミ球 になることからわかる。
一方で、固体中では電子が原子の周期ポテンシャルなどを受ける。したがって、電子はもはや自由電子として振る舞わない。![]() 電子の場合は、自由電子に近いため、フェルミ面はフェルミ球に近い形となる(”fermi surface”で画像検索)。
電子の場合は、自由電子に近いため、フェルミ面はフェルミ球に近い形となる(”fermi surface”で画像検索)。
フェルミ面の形からわかる通り、エネルギーと波数の関係について、もはや ![]() ではない。ただし、エネルギーは波数の関数となるため、
ではない。ただし、エネルギーは波数の関数となるため、
![]()
のように表す。これを分散関係と呼ぶ。
2. 状態密度の導出
以下では ![]() 番目のバンドを表す
番目のバンドを表す ![]() について省略する。したがって、1つのバンドを考えた時の状態密度を求める。最後に
について省略する。したがって、1つのバンドを考えた時の状態密度を求める。最後に ![]() として、全バンドの寄与を考えれば良い。
として、全バンドの寄与を考えれば良い。
考え方・求め方
状態密度は、あるエネルギー ![]() と
と ![]() の間にどれだけの状態が存在しているかを表す。
の間にどれだけの状態が存在しているかを表す。
状態密度の求め方は自由電子のときに状態密度を求めた考え方と同じである。つまり、![]() と
と ![]() の間にある領域の体積(逆空間の体積)を、1つの状態が占める体積
の間にある領域の体積(逆空間の体積)を、1つの状態が占める体積 ![]() で割れば良かった(なぜ?)。
で割れば良かった(なぜ?)。![]() はスピンの自由度、
はスピンの自由度、![]() はセルの体積である。
はセルの体積である。
- 等エネルギー面の間の領域の体積を求めて
- 1状態の占める体積で割る
自由電子の場合は ![]() の球であったため、2つの球面で囲まれる球殻の体積を求めれば良かった。
の球であったため、2つの球面で囲まれる球殻の体積を求めれば良かった。
一般的な場合の求め方は、![]() の等エネルギー面と、それから
の等エネルギー面と、それから ![]() だけ大きなエネルギー
だけ大きなエネルギー![]() を持つ等エネルギー面を用意する。そして、2つの面で囲まれる領域の体積を求めればよい。
を持つ等エネルギー面を用意する。そして、2つの面で囲まれる領域の体積を求めればよい。
以下ではこの計算をしていくが、結論を先に言っておく。領域の体積は
![]()
となる。 したがって、1つのバンドの状態密度は
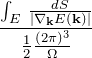
となる。分母は1つの状態が占める逆空間における体積である。
以下、等エネルギー面や ![]() などの説明をしていく。 ほとんどベクトル解析の話になる。
などの説明をしていく。 ほとんどベクトル解析の話になる。
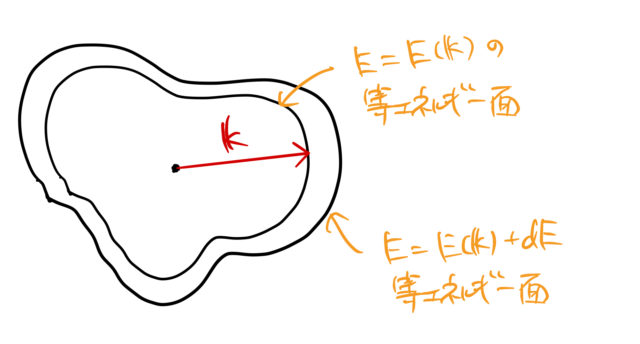
等エネルギー面で囲まれる領域
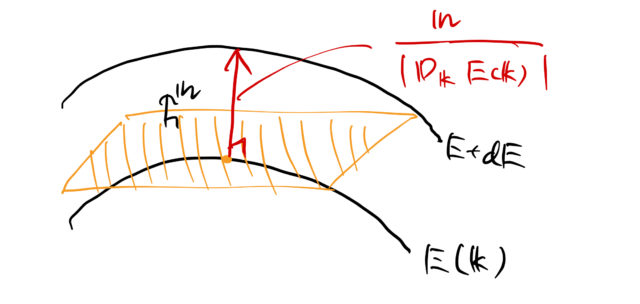
下図のような2つの等エネルギー面を考える。実際には立体的な絵である。
隣の等エネルギー面までの距離を求めたい。そのときに役立つのが勾配 ![]() である。
である。
3次元であるが、等エネルギー面ということは山の高さなどを2次元的に表した等高線と似ている。 そうすると、面と面との「距離」が狭いところと広いところ、どちらが 急勾配 になっているだろうか。
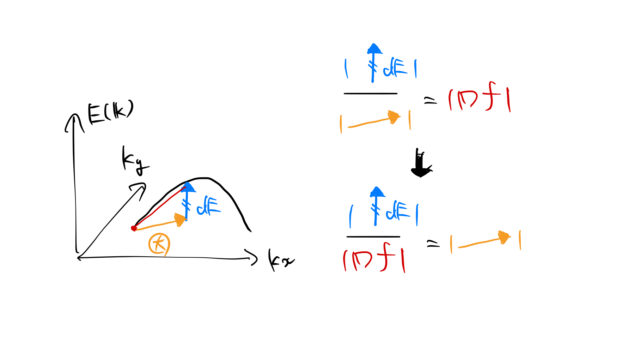
勾配の小さい・大きい
2次元的に見てみよう。![]() だけ高いところへ登る場合を考える。下の図には、勾配が大きい山と勾配が小さい山を描いている。
だけ高いところへ登る場合を考える。下の図には、勾配が大きい山と勾配が小さい山を描いている。
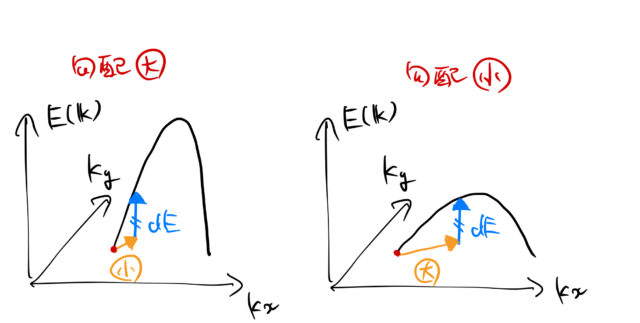
このオレンジ色(![]() 平面上)のベクトルの大きさが面と面の「距離」に対応する。
平面上)のベクトルの大きさが面と面の「距離」に対応する。
明らかに、勾配が大きいほうが間隔が狭いのである。このことは地図の等高線の間隔が狭いほど地形が急峻であることと全く同じである。
なぜ勾配の逆数か?
勾配の大きさを考える場合、曲面の接平面を考えるのと同じである。そのことは、1変数関数と2変数関数の場合を比べればわかる。
まず1変数関数 ![]() のある点
のある点 ![]() の勾配、すなわち、接線の傾きは
の勾配、すなわち、接線の傾きは ![]() に対応する。このときの
に対応する。このときの ![]() の法線の傾きは、
の法線の傾きは、![]() となる(
となる(![]() 2つの直線の傾きの積が-1のときに直線は直交)。
2つの直線の傾きの積が-1のときに直線は直交)。
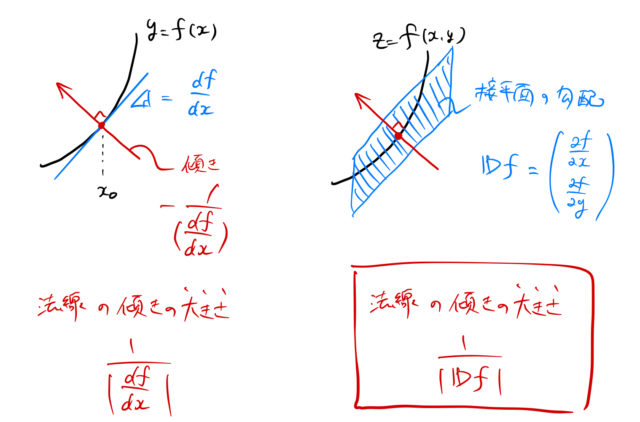
したがって、法線の傾きの大きさは単に絶対値をつければ良い。
![]()
次に、2変数関数 ![]() の場合も同様である。勾配の大きさは接平面の傾きに対応する。
の場合も同様である。勾配の大きさは接平面の傾きに対応する。
そうすると、接平面に垂直な法線の傾きの大きさは、
![]()
となるだろう。これが勾配の逆数となる理由である。 ざっくり描いてしまうと以下のようになる。
したがって、![]() としたときに、隣の面までの「距離」は
としたときに、隣の面までの「距離」は ![]() となる。
となる。
領域の体積
体積は図のように微小体積を用意して、足し合わせていけば良い。 そのときに、![]() ごとに、曲面上に微小面積
ごとに、曲面上に微小面積 ![]() を考える。
を考える。

この微小体積は
![]()
であり、等エネルギー面 ![]() のすべての微小面について積分で足し合わせればよい。これで、2つの等エネルギー面の領域の体積が
のすべての微小面について積分で足し合わせればよい。これで、2つの等エネルギー面の領域の体積が
![]()
と求められる。あとは1状態の占める体積で割って、![]() バンド分足し合わせれば状態密度が求められる。
バンド分足し合わせれば状態密度が求められる。
![]()
3. まとめ
いろいろベクトル解析の説明しているが、状態密度の求め方は
- 等エネルギー面の間の領域の体積を求めて
- 1状態の占める体積で割る
だけである。領域の体積を求めるために勾配(gradient)を駆使したにすぎない。