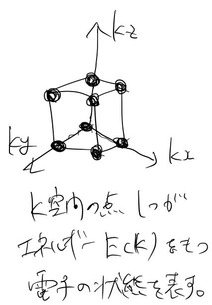
三次元の自由電子(ポテンシャル![]() )のフェルミ球(とくに単純立法の場合)について書こう。
)のフェルミ球(とくに単純立法の場合)について書こう。
ここでは、自由電子のエネルギー固有値、逆格子点(![]() 点)の役割、フェルミ球を作りその中の状態数を求める。逆空間のイメージがつかめていなかった方でも、理解できるように解説していきたい。
点)の役割、フェルミ球を作りその中の状態数を求める。逆空間のイメージがつかめていなかった方でも、理解できるように解説していきたい。
1. 自由電子のエネルギー固有値
時間に依存しないシュレディンガー方程式は、![]() 座標をとると、
座標をとると、
![]()
のように書ける。このとき、自由電子はポテンシャルの影響を受けない(![]() )として、
)として、
![]()
となる。ここで、演算子 ![]() は
は
![]()
で表される。式(*)は、固有値方程式である。したがって、![]() とするのは間違いである。なぜなら、左辺は演算子、右辺は定数となっているからである。
とするのは間違いである。なぜなら、左辺は演算子、右辺は定数となっているからである。
式(*)は、![]() の2階微分が再度
の2階微分が再度 ![]() になる形であるので、微分方程式は容易に解けて、
になる形であるので、微分方程式は容易に解けて、
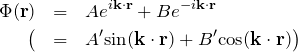
で表される指数関数(三角関数)の形となる。ここで、![]() は波動関数の規格化を満たすような積分定数である。この
は波動関数の規格化を満たすような積分定数である。この ![]() を式(*)に代入すると、
を式(*)に代入すると、
![]()
のように、![]() に置き換わったように見える。式(*)との違いは、左辺の演算子
に置き換わったように見える。式(*)との違いは、左辺の演算子 ![]() が実数の
が実数の ![]() に置き換わったことである。したがって、今度は、
に置き換わったことである。したがって、今度は、
![]()
となる、3次元の自由電子のエネルギー ![]() の関係を得る。
の関係を得る。
2. 逆格子点(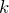 点)の役割
点)の役割
逆格子空間を定義すると、その格子点は ![]() を指定することになる。すなわち、逆格子点を選ぶことは、エネルギー
を指定することになる。すなわち、逆格子点を選ぶことは、エネルギー![]() を持った波動関数
を持った波動関数![]() を選ぶことを意味する。
を選ぶことを意味する。
パウリの排他原理によれば、同じスピンを持つ電子は同じ状態を占有することができない。したがって、各逆格子点で指定される状態はスピン(![]() と
と![]() )の自由度を考慮して、2つの状態が存在する。
)の自由度を考慮して、2つの状態が存在する。
実空間の立方晶系の格子定数を![]() とすると、逆格子点の間隔は
とすると、逆格子点の間隔は ![]() で与えられる (
で与えられる (![]() は周期境界条件により導入される)。したがって、格子点1個が逆格子空間で占める体積(図の立方体の体積)は
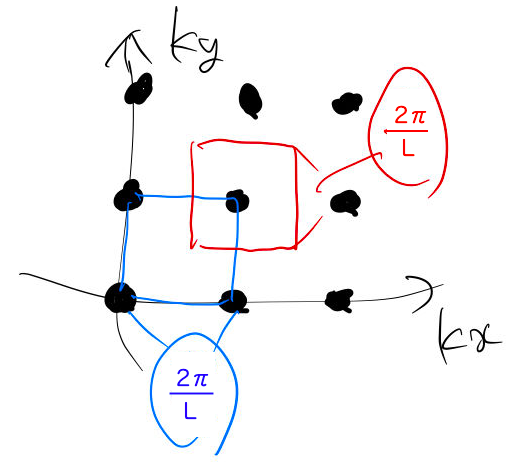
は周期境界条件により導入される)。したがって、格子点1個が逆格子空間で占める体積(図の立方体の体積)は ![]() となる。
となる。
立方体に格子点が8個もあるのが分かりにくいという方は、下の正方形を見て欲しい。正方形の面積は、青であろうが赤であろうが、同じである。
3. フェルミ球を作る
自由電子の場合、エネルギー ![]() は 式(**)で与えられた。絶対零度(
は 式(**)で与えられた。絶対零度(![]() K)では、エネルギーの小さい順に電子が状態を占めることがわかる。エネルギーは
K)では、エネルギーの小さい順に電子が状態を占めることがわかる。エネルギーは ![]() に比例するので、
に比例するので、![]() の大きさ
の大きさ![]() の小さいものから逆格子空間(
の小さいものから逆格子空間(![]() 空間)の逆格子点を選んでいくと球に近くなる。
空間)の逆格子点を選んでいくと球に近くなる。
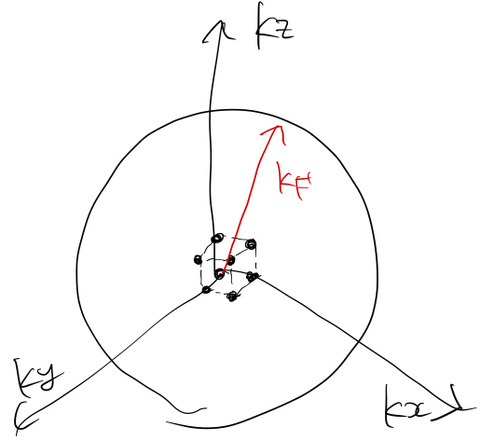
一番大きなエネルギー(フェルミエネルギー(![]() ))を取る
))を取る ![]() をフェルミ波数
をフェルミ波数 ![]() と呼ぶ。
と呼ぶ。![]() も逆格子点の上にあるので厳密な球にはならないが、
も逆格子点の上にあるので厳密な球にはならないが、![]() は逆格子点の間隔に比べて大きいのでほぼ球体となっている。すなわち、図のフェルミ球は立方体に比べて非常に大きい。
は逆格子点の間隔に比べて大きいのでほぼ球体となっている。すなわち、図のフェルミ球は立方体に比べて非常に大きい。
*本当に球に見えるか?については実際に計算してみるとわかる。例えば、Cuなどの格子定数と密度などから ![]() 、
、![]() 程度である。
程度である。
** 直感的にイメージするためには、1モルの1価金属あたり ![]() 個の電子があるので、
個の電子があるので、![]() 分のレゴブロックで球を作ってやれば良い。
分のレゴブロックで球を作ってやれば良い。
4. フェルミ球の中にある状態の数(単純立方)
1つの逆格子点(![]() 点)はスピンを考慮して、2つの状態を占めることを説明した。すなわち、立方晶の場合、2つの状態は逆格子空間で、
点)はスピンを考慮して、2つの状態を占めることを説明した。すなわち、立方晶の場合、2つの状態は逆格子空間で、
![]()
の体積を占める。また、フェルミ球の体積は、
![]()
で与えられる。 求めるフェルミ球内の状態数 ![]() は「フェルミ球に詰められる立方体の数の2倍」と同じである。つまり、(2)を(1)で除して2倍(スピンの自由度)すればよく、
は「フェルミ球に詰められる立方体の数の2倍」と同じである。つまり、(2)を(1)で除して2倍(スピンの自由度)すればよく、
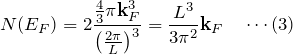
となる。フェルミ波数 ![]() はフェルミエネルギー
はフェルミエネルギー![]() を用いて、
を用いて、
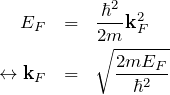
である。 これを式(3)へ代入して、
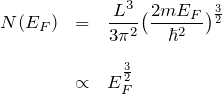
となる。これにより、3次元の自由電子についてフェルミエネルギーの状態数 ![]() はフェルミエネルギー
はフェルミエネルギー![]() に比例するという重要な結果を得た。いま、フェルミ半径
に比例するという重要な結果を得た。いま、フェルミ半径![]() のフェルミ球を考えたが、任意のエネルギー(または任意の波数
のフェルミ球を考えたが、任意のエネルギー(または任意の波数![]() )についても同様に、
)についても同様に、
![]()
となることが確認される。この関係から、容易に、
![]()
となることがわかる。これより3次元の自由電子については状態密度がエネルギーの1/2乗に比例することがわかる。