固体物理においては結晶を扱う。したがって、結晶格子は周期的に並んでいるという理想的な状態を考える。実際の結晶では有限的で表面があるために、なんとか表面を考えないようにしたい。こうして考え出されたのが、周期境界条件である。
表面の条件を考えたく無い→周期境界条件
目次
1. 1次元の場合
表面がない無限結晶を考える方が理論的に扱いやすい。そういうわけで周期境界条件を導入する。1次元の場合から考えていく。
1.1 周期境界条件の導入
図左のベンゼンは6つの炭素原子の間を電子が往来する。また、![]() 個の原子を円環に置いた場合も周期境界条件が満たされていると言える。
個の原子を円環に置いた場合も周期境界条件が満たされていると言える。
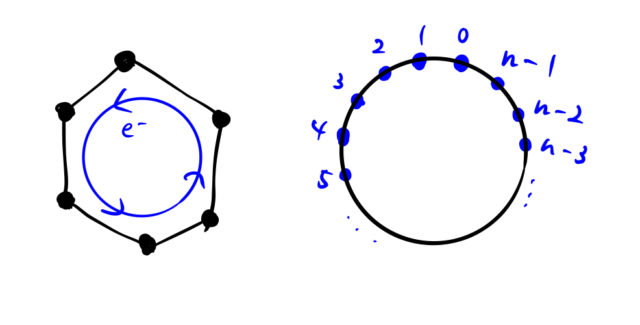
一方で無限に続く結晶格子の場合は0番目の原子から
…, 0, 1, 2, 3, …, n-1, n, n+1, …
と結晶格子は無限に続いている(図の上)。![]() 個だけ隣の原子については自分自身と同じであるという、周期境界条件(ボルン=フォン・カルマン境界条件)を課す(図の下)。
個だけ隣の原子については自分自身と同じであるという、周期境界条件(ボルン=フォン・カルマン境界条件)を課す(図の下)。
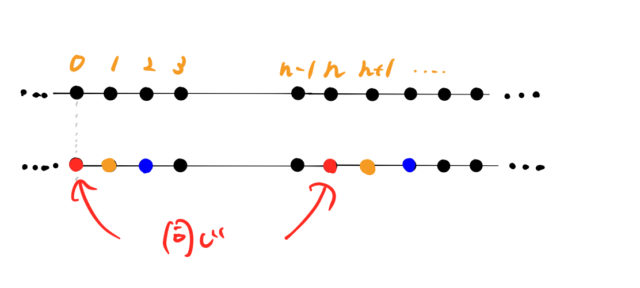
結晶格子の間隔(図の格子点間隔)を ![]() とすれば、位置を表す連続変数
とすれば、位置を表す連続変数 ![]() を用いて、
を用いて、
![]()
のようになる。![]() は電子の波動関数を表している。0番目の格子点から
は電子の波動関数を表している。0番目の格子点から ![]() 番目の格子点までを系の大きさ
番目の格子点までを系の大きさ ![]() とすると、
とすると、 ![]() となる。以上を下にまとめた。
となる。以上を下にまとめた。
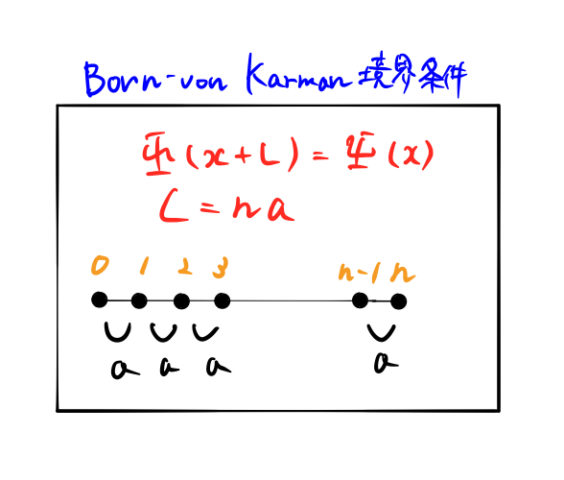
1.2 規格化できるようになる
周期境界条件により規格化ができるようになった。というのも、周期境界条件がない場合の規格化条件は
![]()
であり、無限の積分になる。しかし周期境界条件により、問題は有限の積分になった。すなわち、積分区間 ![]() で
で ![]() の積分が可能となる。
の積分が可能となる。
1.3 波数kとは
周期境界条件の導入により波動関数 ![]() が周期的であるという条件が課された。フーリエ級数の考え方によれば、周期
が周期的であるという条件が課された。フーリエ級数の考え方によれば、周期 ![]() の周期的な関数は同じ周期
の周期的な関数は同じ周期 ![]() の周期関数で展開できる。
の周期関数で展開できる。
周期 ![]() の平面波を用意しよう。
の平面波を用意しよう。![]() (
(![]() )は周期
)は周期 ![]() の関数である(
の関数である(![]() で確認)。
で確認)。
したがって、![]() を満たす
を満たす ![]() は
は ![]() で展開できる。ここで指数関数のごちゃごちゃした部分を波数
で展開できる。ここで指数関数のごちゃごちゃした部分を波数 ![]() とおく。
とおく。
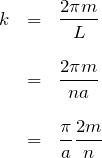
![]() は整数であるため、波数
は整数であるため、波数 ![]() は離散的な値しかとらない。また、
は離散的な値しかとらない。また、![]() の形は以下の第一ブリルアンゾーン(1stBZ)を作る単位として重要である。
の形は以下の第一ブリルアンゾーン(1stBZ)を作る単位として重要である。
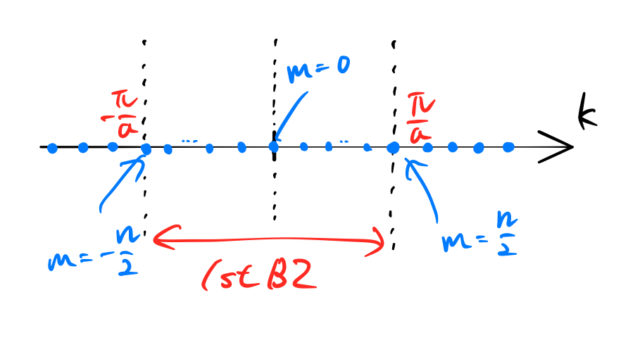
1stBZの外にある逆格子点は1stBZの中の点に移すことができる。したがって、可能な波の数 ![]() は、
は、
![]()
の ![]() 個である。右側に等号がないのは、BZ境界上にある
個である。右側に等号がないのは、BZ境界上にある ![]() は
は ![]() へ移すことができるためである。あるいは隣のBZの境界とみる。
へ移すことができるためである。あるいは隣のBZの境界とみる。
おおよそ波数 ![]() の理解は下のように考えるのが良い。
の理解は下のように考えるのが良い。
- 波数
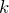 は離散的
は離散的 - 取りうる波数
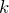 は
は 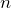 個ある
個ある 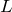 が大きいほど
が大きいほど 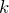 の間隔は小さい
の間隔は小さい- 波数
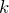 は「波の形」を指定する
は「波の形」を指定する
1.4 可能な波の数とは
最も単純な場合として ![]() のときを考える。このとき
のときを考える。このとき ![]() である。
である。
![]() のとき取りうる
のとき取りうる ![]() の数は2個である。
の数は2個である。
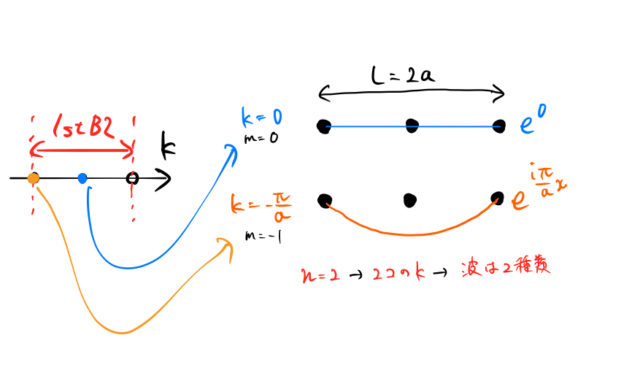
したがって図のように、波としては2種類の波がある。![]() の場合は周期境界条件を満たす波動関数は、2個の平面波で展開できる。
の場合は周期境界条件を満たす波動関数は、2個の平面波で展開できる。
これは格子振動の場合も同じである。基準となる![]() 個のモードを重ね合わせで格子振動を表すことができる。
個のモードを重ね合わせで格子振動を表すことができる。
2. 3次元の場合
3次元への拡張は簡単である。
2.1 3次元への拡張
系が辺 ![]() の大きな立方体とする。このときの
の大きな立方体とする。このときの ![]() の周期境界条件は、
の周期境界条件は、
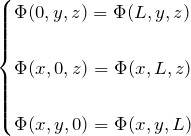
としてやればよい。波数も波数ベクトル ![]() になる。それぞれ、
になる。それぞれ、
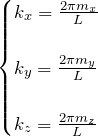
であり、![]() は1stBZ内に取れば良い。
は1stBZ内に取れば良い。
2.2 系のサイズLが非常に大きいとき
![]()
であるため、![]() のときに波数ベクトル
のときに波数ベクトル ![]() は連続的に扱って良い。すなわち、
は連続的に扱って良い。すなわち、![]() で置き換えて良い。
で置き換えて良い。
積分の前の因子 ![]() は
は ![]() 空間で 1つの
空間で 1つの![]() 点が占める体積である。
点が占める体積である。
3. まとめ
周期境界条件を端と端をつなげるだけで終わってはならない。波数 ![]() がどうなるかを考える必要がある。
がどうなるかを考える必要がある。
途中にあった「波の重ね合わせ」の概念は物理において非常に重要な概念である。まずは、波動関数や格子振動でその描像に慣れておくのが良いだろう。