逆格子空間での ![]() は積分で置き換えた方が解析的に計算しやすいときがある。よく見る下の置き換えを証明して、わかりやすく説明する。
は積分で置き換えた方が解析的に計算しやすいときがある。よく見る下の置き換えを証明して、わかりやすく説明する。
和を積分で置き換える
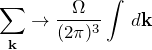
1. 適用条件
和を積分に置き換えて良いのは、逆格子点の間隔が小さいときである。逆格子点の間隔は周期境界条件が与えられているとき、![]() である。
である。
系のサイズ ![]() が非常に大きいときは、離散的な逆格子点を連続とみなしてよく、
が非常に大きいときは、離散的な逆格子点を連続とみなしてよく、![]() を積分で置き換えることができる。
を積分で置き換えることができる。
2. 和を積分で書き換える
2.1 逆格子点1個の占める体積
図の(a)に示すように逆格子点の間隔は ![]() であった。
であった。
注意:![]() 単位のブリルアンゾーンと混同してはならない。この
単位のブリルアンゾーンと混同してはならない。この ![]() 点は1stブリルアンゾーン内にある
点は1stブリルアンゾーン内にある ![]() 点である。ざっくり言うと、周期境界条件によって1stBZ内に間隔
点である。ざっくり言うと、周期境界条件によって1stBZ内に間隔 ![]() の
の ![]() 点のメッシュができる。
点のメッシュができる。
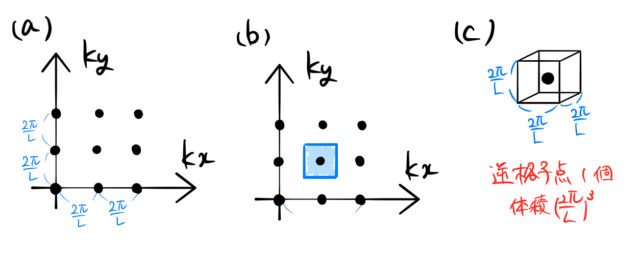
図(b)は逆格子点1個が占める体積を表している。![]() 点の間隔が
点の間隔が ![]() であるため、図(c) のように体積は
であるため、図(c) のように体積は ![]() である。
である。
2.2 逆格子空間内の体積を2通りで表す
適当な立方体の体積 ![]() を和で表す。図左のように27個(
を和で表す。図左のように27個(![]() 平面(
平面(![]() )で9個)の格子点が含まれる立方体を考える。
)で9個)の格子点が含まれる立方体を考える。
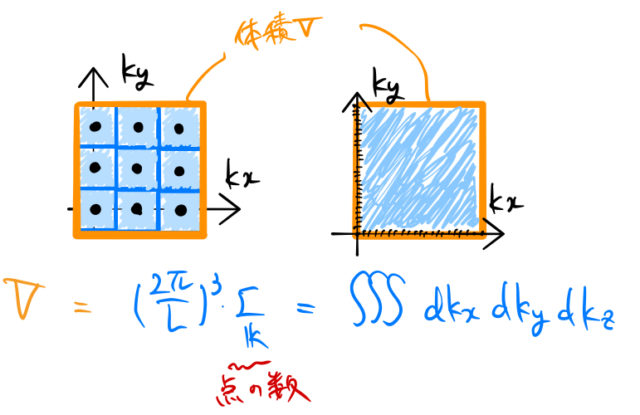
逆格子点1個あたりの体積が ![]() であったため、体積
であったため、体積 ![]() はその体積に逆格子点の数(例では27個)をかければよい。
はその体積に逆格子点の数(例では27個)をかければよい。
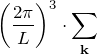
一方で体積 ![]() は図の右のように3重積分で表すことができる。
は図の右のように3重積分で表すことができる。
![]()
これらは同じ体積であるために、![]() の関係が求められる。
の関係が求められる。
和を積分で置き換える
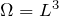 とした。
とした。
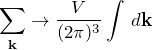
3. まとめ
教科書によっては「和を積分で置き換える」だけ書いてあったりして初学者は戸惑うかもしれない。誰も教えてくれなかったりもするため、ここにその求め方だけ残しておこう。