一様な電場を加えたとき、原子のエネルギー準位がどのような影響を受けるかを考える(シュタルク効果)。電場 ![]() の方向を
の方向を ![]() 方向にとり、エネルギー準位の分裂とエネルギーのずれを求める。このとき、電場の大きさを
方向にとり、エネルギー準位の分裂とエネルギーのずれを求める。このとき、電場の大きさを ![]() として
として
![]()
の摂動ハミルトニアンを考えれば良い。計算には波動関数の対称性を使うと良い。
目次
2s,2p 状態について
水素原子の状態は主量子数 ![]() , 軌道角運動量の大きさ
, 軌道角運動量の大きさ ![]() , その
, その ![]() 成分
成分 ![]() で指定できる。このように指定された状態を
で指定できる。このように指定された状態を
![]()
とする。![]() は動径方向の関数、
は動径方向の関数、![]() は球面調和関数であった。以下では
は球面調和関数であった。以下では ![]() 状態(
状態(![]() )について考え、それ以外の状態とは混成しないとする。 ここでの「エネルギーのずれ」とは、電場がないときの非摂動ハミルトニアン
)について考え、それ以外の状態とは混成しないとする。 ここでの「エネルギーのずれ」とは、電場がないときの非摂動ハミルトニアン ![]() のエネルギー固有値
のエネルギー固有値 ![]() と、
と、![]() 方向の電場により縮退が解けて分裂したエネルギー
方向の電場により縮退が解けて分裂したエネルギー ![]() とのずれである。
とのずれである。
空間反転とパリティ
計算にはパリティの対称性を使うので、簡単にまとめておく。 空間反転の演算子 ![]() は
は ![]() とする。したがって、
とする。したがって、![]() であり、
であり、![]() である。
である。
![]()
である。![]() であり、
であり、![]() と
と ![]() は同時固有状態をもつため、
は同時固有状態をもつため、
![]()
![]() は
は ![]() の固有値で
の固有値で ![]() である。
である。![]() の固有値は
の固有値は ![]() にのみ依存する。したがって、
にのみ依存する。したがって、![]() と
と ![]() は同じパリティであるが、
は同じパリティであるが、![]() と
と ![]() は異なるパリティである。
は異なるパリティである。
水素原子の状態 (n=2)
動径関数と球面調和関数の具体的な形を用いて、3次元の極座標表示で ![]() の波動関数を表すと、
の波動関数を表すと、
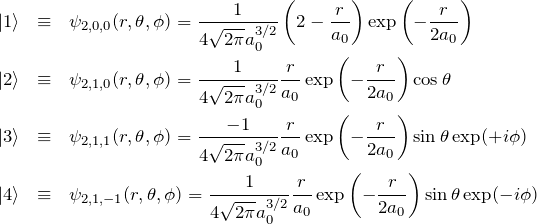
となる。ここで、![]() はボーア半径である。
はボーア半径である。![]() における波動関数のパリティ
における波動関数のパリティ ![]() と
と ![]() の値を整理しておく。
の値を整理しておく。
| +1 | 0 | ||
| −1 | 0 | ||
| −1 | 1 | ||
| −1 | −1 |
摂動ハミルトニアンの行列要素
行列表現
![]() について、上の
について、上の ![]() の4つの状態
の4つの状態 ![]() を基底として行列で表現し、固有値を求めることでエネルギーのずれを求めることができる。行列を具体的に書いておく。
を基底として行列で表現し、固有値を求めることでエネルギーのずれを求めることができる。行列を具体的に書いておく。
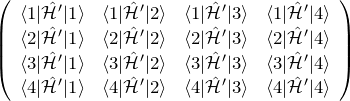
行列の ![]() 成分は
成分は
![]()
のように計算できる。しかし、上の16個の要素についてこの積分計算を実行するのは大変に見える。しかしながら、以下に説明するように、対称性から上の行列要素のほとんどが0になる。
対称性1: eEz=eErcosθと空間反転
摂動ハミルトニアン ![]() と 空間反転
と 空間反転 ![]() について調べる。結論から言うと、空間反転によって
について調べる。結論から言うと、空間反転によって ![]() となるので、
となるので、
![]()
が成立する。これは ![]() のパリティが同じであれば、
のパリティが同じであれば、![]() になることを意味する。
になることを意味する。
空間反転により、
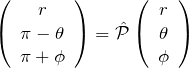
である。これより、動径関数
「空間反転とパリティ」 に示したように、
![]()
である。ここで、固有値は
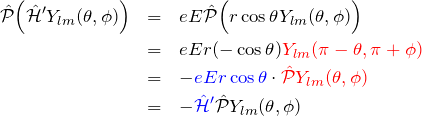
よって、
![]()
となる。また、状態
状態
![]()
とする。式(1)から、
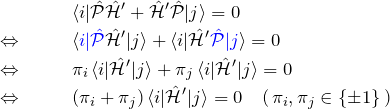
となる。これは
対称性2: eEz=eErcosθとz軸回転
摂動ハミルトニアン ![]() と
と ![]() について調べる。
について調べる。![]() も
も ![]() も
も ![]() 軸周りの回転対称性を持つ。したがって、これらの演算子は交換するので交換関係は
軸周りの回転対称性を持つ。したがって、これらの演算子は交換するので交換関係は
![]()
である。これより、![]() 成分である
成分である ![]() が異なる場合は行列要素が
が異なる場合は行列要素が ![]() になることがわかる。
になることがわかる。
* 演算子が交換することは ![]() であり、
であり、![]() を用いれば、
を用いれば、![]() となることからわかる。
となることからわかる。
![]()
となる。次に、
![]()
となる。式(2)から
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\braket{i|\left[\hat{\mathcal H}',\hat{l}_z\right]|j}=0\\ \Leftrightarrow\quad&& \braket{i|\hat{\mathcal H}'\textcolor{blue}{\hat{l}_z|j}}- \braket{\textcolor{blue}{i|\hat{l}_z}\hat{\mathcal H}'|j}=0\\ \Leftrightarrow\quad&& (m_i-m_j)\braket{i|\hat{\mathcal H}'|j}=0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-5c39304c27f18bbb9d04a2afc4b33bd7_l3.png)
となる。これは
0でない行列要素
上の対称性より ![]() にならない要素は
にならない要素は
- パリティ(
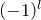 の値) が異なる
の値) が異なる -
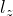 成分
成分 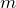 が同じ
が同じ
である。これを満たす行列要素は ![]() のみである。
のみである。
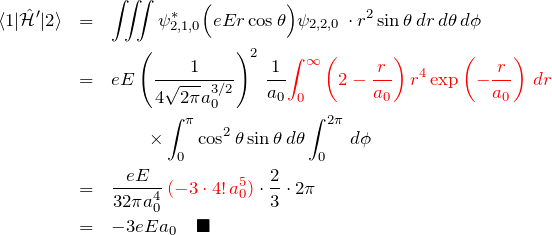
途中の ![]() に関する積分計算は「∫r^n exp(-αr)drの積分」を利用すると早い。
に関する積分計算は「∫r^n exp(-αr)drの積分」を利用すると早い。
![]()
について両辺を
![]()
を得る。これより、
固有値からエネルギーのずれを計算
固有値・固有関数の計算
以上の結果をまとめて、![]() を
を ![]() を基底とした行列で表すと
を基底とした行列で表すと
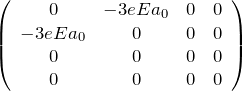
のようになり、対称性よりほとんどの要素がゼロになる。永年方程式より1次の摂動エネルギーに対応する固有値 ![]() を求める。
を求める。
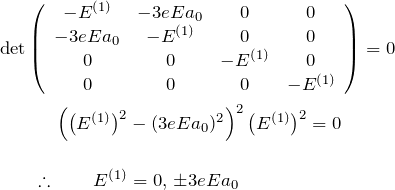
もともと ![]() の4つの状態
の4つの状態 ![]() のエネルギーは縮退していたが、一様な電場による摂動
のエネルギーは縮退していたが、一様な電場による摂動 ![]() を受けて、その縮退のうち2つが解ける(シュタルク効果)。つまり、行列の左上ブロックについて、
を受けて、その縮退のうち2つが解ける(シュタルク効果)。つまり、行列の左上ブロックについて、![]() となり縮退は解けている。
となり縮退は解けている。
左上ブロック部分の固有関数を ![]() の線形結合
の線形結合
![]()
とする。このとき、
![]()
である。それぞれの固有エネルギーに関して、固有関数を求める。規格化した形で ![]() を求めると、
を求めると、
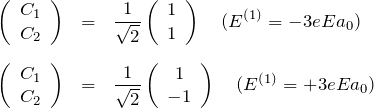
具体的な形で書くと、縮退が解けエネルギーの高くなった固有状態 ![]() と低くなった固有状態
と低くなった固有状態 ![]() はそれぞれ、
はそれぞれ、
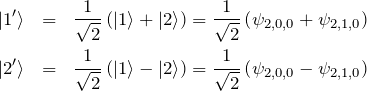
である。一方で、行列の右下ブロックについては縮退は解けない(エネルギーのずれ ![]() である)。この固有状態
である)。この固有状態 ![]() は2重縮退している。縮退しているため、固有関数は
は2重縮退している。縮退しているため、固有関数は ![]() の線形結合によって表される。
の線形結合によって表される。
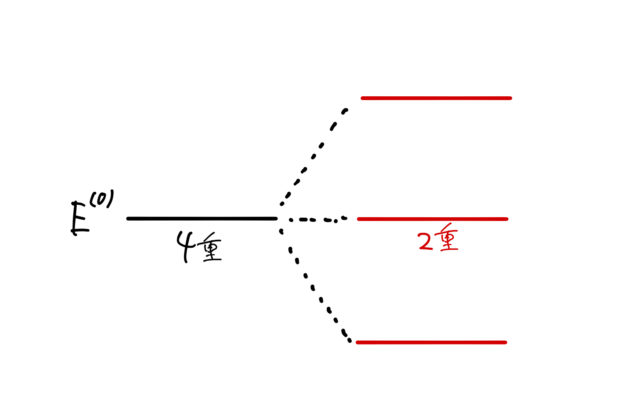
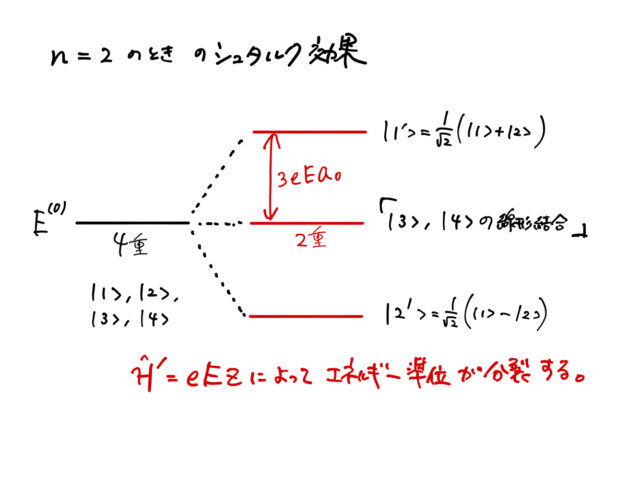
エネルギー準位の分裂の図示
最後に得られた結果を図示する。はじめ電場のない場合 ![]() のときにエネルギーが
のときにエネルギーが ![]() にあったとする。この状態は
にあったとする。この状態は ![]() の4重に縮退している(図の左)。
の4重に縮退している(図の左)。
![]() 方向の一様な電場によって縮退が解ける。このとき、分裂によるエネルギーのずれは上で計算した
方向の一様な電場によって縮退が解ける。このとき、分裂によるエネルギーのずれは上で計算した ![]() である(図の右)。
である(図の右)。
* 1s軌道に対して電場の効果を考える場合、![]() で
で ![]() を挟んで摂動のエネルギーを計算すればよい。このとき、
を挟んで摂動のエネルギーを計算すればよい。このとき、![]() と
と ![]() はもちろんパリティが同じなので、
はもちろんパリティが同じなので、
![]()
である。よって1次の摂動によるエネルギーのずれは0である。電場によるエネルギーのずれを求めるためには2次の摂動を考えなければならない。