気体分子論や量子力学など物理でよく出てくる積分をまとめておく。その簡単な導出方法も示しておく。
ポイント
![]()
ここで、![]() は負でない整数とする。
は負でない整数とする。![]() と積分変数を変換すれば、ガンマ関数を用いて計算ができるが、ここでは工夫して計算する方法を紹介する。
と積分変数を変換すれば、ガンマ関数を用いて計算ができるが、ここでは工夫して計算する方法を紹介する。
目次
積分: ∫r^n exp(-αr)dr
以下、![]() は負でない整数とする。
は負でない整数とする。
ガンマ関数 Γ(n)
![]() のときはガンマ関数
のときはガンマ関数 ![]() そのものである。
そのものである。![]() の積分計算は部分積分を繰り返すことで簡単に求めることができる。
の積分計算は部分積分を繰り返すことで簡単に求めることができる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Gamma(n)&\equiv& \int_0^\infty r^{n-1}\exp(-r)\, dr\\ &=&\cancel{\left[-r^{n-1}\exp(-r)\right]_0^\infty} + (n-1)\int_0^\infty r^{n-2} \exp(-r)\,dr\\ &=&(n-1)\Gamma(n-1)\\ &=&(n-1)(n-2)\Gamma(n-2)\\ &=&\cdots\\ &=&(n-1)(n-2)\cdot \cdots \cdot 2\cdot 1\cdot\Gamma(1)\\ &=&(n-1)!\quad(\because \,\Gamma(1)=1) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-fdbc241e00f31568edead4ebafc4a49b_l3.png)
ここで、![]() は負でない正の整数とした。
は負でない正の整数とした。
∫exp(-αr)dr
直接計算する:
![Rendered by QuickLaTeX.com \begin{eqnarray*} I(\alpha)&\equiv& \int_0^\infty \exp(-\alpha r)\, dr\\&=&\left[-\frac{1}{\alpha}\exp(-\alpha r)\right]_0^\infty\\&=&\frac{1}{\alpha}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8e002718f2b794d97adc5912aaa1e80d_l3.png)
(別)ガウス関数を利用する: ![]() と変換して、
と変換して、![]() から、
から、
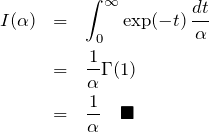
ポイント
![]()
∫r exp(-αr)dr
上の結果を利用する。(*)の左辺について、![]() で微分すると
で微分すると ![]() の前に
の前に![]() が現れる。
が現れる。
![]()
右辺は ![]() の微分であるため
の微分であるため ![]() となる。したがって、
となる。したがって、
ポイント
![]()
(別)ガウス関数を利用する(![]() )。
)。
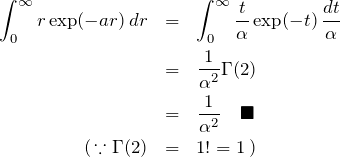
∫r^2 exp(-αr)dr
(*)を2回 ![]() で微分する。
で微分する。
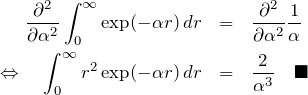
(別)ガウス関数を利用する(![]() )。
)。
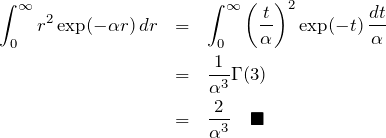
ポイント
![]()
∫r^n exp(-αr)dr
(*)を ![]() 回
回 ![]() で微分する。
で微分する。
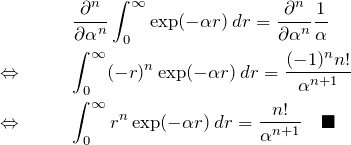
(別)ガウス関数を利用する(![]() )。
)。
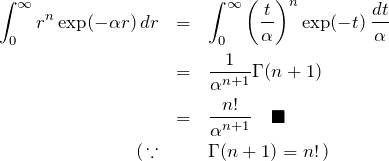
ポイント
![]()
簡単な使用例
簡単な計算例を挙げておく。
1s軌道の波動関数の規格化
![]() 軌道
軌道 ![]() は以下のように球対称で角度成分を含まない。
は以下のように球対称で角度成分を含まない。
![]()
ここで、![]() はボーア半径、規格化定数を
はボーア半径、規格化定数を ![]() とする。波動関数を規格化するために全空間で積分する。(
とする。波動関数を規格化するために全空間で積分する。(![]() に注意する。)
に注意する。)
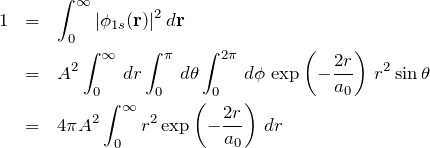
ここで、
![]()
について、![]() ,
, ![]() として
として
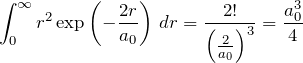
となる。したがって、
![]()
となる。規格化された ![]() 軌道の波動関数は
軌道の波動関数は
![]()
となる。