1体問題、2体問題、![]() 体問題の運動方程式について簡単にまとめておく。
体問題の運動方程式について簡単にまとめておく。
質点と運動方程式
![]() 体問題では、
体問題では、![]() 個の質点の運動方程式を考える。物理で考える場合は、
個の質点の運動方程式を考える。物理で考える場合は、![]() の1体問題、
の1体問題、![]() の2体問題、
の2体問題、![]() が3以上の多体問題 しかない。われわれ人間は2体問題まで解くことかでき、3体問題以上は魔界である。
が3以上の多体問題 しかない。われわれ人間は2体問題まで解くことかでき、3体問題以上は魔界である。
* 「動物が数を数えるかどうか?」という問題について、興味深い最近の話題を紹介しておく。
ナショナルジオグラフィック:『「数を数える能力』実は多くの動物に、研究成果』
1体問題
1体問題では
![]()
を解けば良い。この式はベクトル ![]() で表された3次元の形であり、方程式自体は3つあるが、
で表された3次元の形であり、方程式自体は3つあるが、![]() が与えられれば解くことができる。
が与えられれば解くことができる。![]() は質点の位置のみに依存するとすれば、
は質点の位置のみに依存するとすれば、![]() の関数になる。
の関数になる。
ローレンツ力など質点の速度 ![]() に依存する力や、時間に依存する力もあるため、一般には
に依存する力や、時間に依存する力もあるため、一般には ![]() と書く。しかし、ここでは多体問題の性質を見ることを目的とするため、以下では質点の座標のみに依存する力を考えていく。
と書く。しかし、ここでは多体問題の性質を見ることを目的とするため、以下では質点の座標のみに依存する力を考えていく。
また、上の運動方程式は(線形の)2階微分方程式である。したがって、一般解には積分定数が2個含まれ、その分の不定性がある。積分定数を決定するためには、初期条件として初期位置 ![]() 、初期速度
、初期速度 ![]() を与えてやれば良い。この6つの条件があれば、運動方程式により以後(
を与えてやれば良い。この6つの条件があれば、運動方程式により以後(![]() )または以前(
)または以前(![]() )の運動は決定できる。このようにニュートン力学は決定論的である。
)の運動は決定できる。このようにニュートン力学は決定論的である。
2体問題
続いて2体問題の場合を考える。2つの質点の間に相互作用がない場合は、質点1に働く力は質点2(![]() )とは無関係である。したがって、
)とは無関係である。したがって、![]() と書ける。質点2に働く力も同様に
と書ける。質点2に働く力も同様に ![]() と書ける。このとき、
と書ける。このとき、
![]()
である。この式は1体問題の運動方程式が単に2つあるだけで、それぞれの質点について運動方程式を解いてやればよい。このように相互作用がない場合は、質点が独立に運動していることがわかる。
つぎに、2質点の間に相互作用がある場合を考える。たとえば万有引力が働いているとすれば、このような相互作用は ![]() のように、2質点の距離に依存するはずである。一般的には、質点1に働く力は
のように、2質点の距離に依存するはずである。一般的には、質点1に働く力は ![]() のみでなく、
のみでなく、![]() にも依存する。したがって運動方程式は
にも依存する。したがって運動方程式は
![]()
のように書かれる。これは相互作用がない場合と異なり、質点が独立に運動しないことをあらわしている。
2体問題を解くためには質点1に働く力を、
-
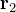 に依存しない外力
に依存しない外力 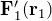
-
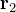 に依存する内力(相互作用)
に依存する内力(相互作用) 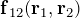
に分離する。また質点2についても
-
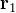 に依存しない外力
に依存しない外力 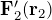
-
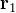 に依存する内力(相互作用)
に依存する内力(相互作用) 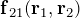
に分離する。ここで作用反作用の法則より、
![]()
である。
これらを用いて運動方程式を書き直すと
![]()
となる。2式を足すと内力 ![]() が消え、重心(質点中心、慣性中心)
が消え、重心(質点中心、慣性中心)![]()
![]()
に関する運動方程式を得ることができる。もう一つの運動方程式として、相対座標 ![]() に関する運動方程式を得ることができる。それぞれ簡単にまとめておくと、
に関する運動方程式を得ることができる。それぞれ簡単にまとめておくと、
![]()
である。ここで、![]() は全質量、
は全質量、![]() は換算質量と呼ばれる。
は換算質量と呼ばれる。
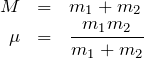
以上のように2つの質点の運動方程式を解く問題は、
-
重心座標
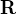 に関する運動方程式
に関する運動方程式 -
相対座標
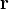 に関する運動方程式
に関する運動方程式
の2つの問題に帰着される。
N体問題
質点間に相互作用がない ![]() 体問題の運動方程式も
体問題の運動方程式も ![]() は
は ![]() のみ関数なので
のみ関数なので
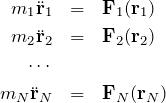
となる。2体問題のところで見たように、![]() 個の質点は独立に運動することができる。したがって、1体問題が
個の質点は独立に運動することができる。したがって、1体問題が![]() 個あるのと同等なので、容易に解くことができる。
個あるのと同等なので、容易に解くことができる。
次に相互作用がある場合について考える。質点 ![]() の質量を
の質量を ![]() , 座標を
, 座標を ![]() , 質点に働く外力を
, 質点に働く外力を ![]() , 質点
, 質点 ![]() が与える内力を
が与える内力を ![]() とすると、質点
とすると、質点 ![]() に対する運動方程式は
に対する運動方程式は
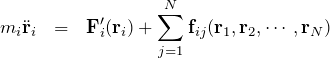
である。したがって、![]() 個の質点に対する
個の質点に対する ![]() 個の運動方程式は
個の運動方程式は
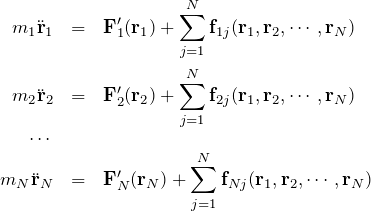
ここで、作用反作用の法則より
![]()
の関係がある。したがって、上の運動方程式を全て足すと、2体問題の場合と同様に内力 ![]() の項は消える。よって
の項は消える。よって
![]()
となる。外力の和 ![]() , 全質量
, 全質量 ![]() , 重心座標
, 重心座標
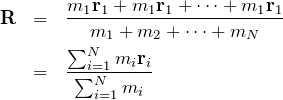
を用いて、
![]()
となる。この式からわかるように系全体に働く外力の和が0 (![]() ) のときには、
) のときには、
![]()
となる。この ![]() は
は
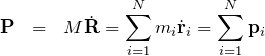
より![]() 個の質点の運動量の和を表す。したがって、
個の質点の運動量の和を表す。したがって、![]() が一定であることは運動量保存則に他ならない。
が一定であることは運動量保存則に他ならない。
何が問題を複雑にしていたか?
![]() 体問題について、問題が複雑になっている原因は質点に働く力に他の質点の位置(や速度)に依存した相互作用が含まれることである。その相互作用が小さくて無視できる場合には、質点はそれぞれ独立に運動するため運動方程式は解ける。このときの解は、相互作用の寄与を無視しているので近似的なものである。
体問題について、問題が複雑になっている原因は質点に働く力に他の質点の位置(や速度)に依存した相互作用が含まれることである。その相互作用が小さくて無視できる場合には、質点はそれぞれ独立に運動するため運動方程式は解ける。このときの解は、相互作用の寄与を無視しているので近似的なものである。
相互作用の寄与が小さい場合において、もう少し精度の良い解を求めるためのアプローチとして摂動論がある。これは相互作用がない場合の解が主要な解であることを利用して、その解に小さな相互作用による影響を考慮して修正を加える方法である。これもまた近似解である。
他には、多体問題を回避するために相互作用を平均化してしまう方法がある(平均場近似)。この手法では、自分が受ける相互作用が自分の座標(や速度)のみで書くことができる。これにより、多体問題を解くことを困難にしていた他の質点の座標について考えなくて済む。平均場近似における平均化の過程では、自分自身の座標が他の質点の座標にも影響を及ぼすため、方程式は自己無撞着(self-consistent )に解く必要がある。また、平均場近似の問題点として、「平均化」する操作により局所的な効果(多体の効果)が消えてしまうことがある。