まずフーリエ級数では関数 ![]() を三角関数で展開する。ここではフーリエ級数における三角関数の以下の直交性を示そう。
を三角関数で展開する。ここではフーリエ級数における三角関数の以下の直交性を示そう。
フーリエ級数で一番大事な式
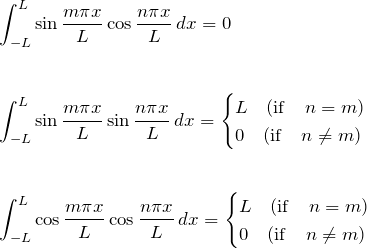
![]() の周期
の周期 ![]() の三角関数についての直交性であるが、
の三角関数についての直交性であるが、![]() などの場合は
などの場合は ![]() とすればよい。
とすればよい。
導出に使うのは下の三角関数の公式:
加法定理
![]()
からすぐに導かれる、
積→和
![Rendered by QuickLaTeX.com \begin{eqnarray*} \sin a \sin b &=& \frac{1}{2}\left[ \sin(a+b)+\sin(a-b) \right]\\\\ \cos a \cos b &=&\frac{1}{2}\left[ \cos(a+b)+\cos(a-b) \right]\\\\ \sin a \sin b &=&\frac{1}{2}\left[ -\cos (a+b)+\cos (a-b) \right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-c748c1bf365cef9cc74113eefe432769_l3.png)
以下の証明では ![]() と積分変数を置き換える。このとき、
と積分変数を置き換える。このとき、![]() で積分区間は
で積分区間は ![]() から
から ![]() になる。
になる。
直交性1
![]()
【証明】
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-L}^{L} \sin \frac{n\pi x}{L} \cos \frac{n\pi x}{L} \, dx &=& \int_{-\pi}^{\pi}\sin 2nx' \left( \frac{L}{\pi} \,dx' \right)\\\\ &=& \frac{L}{\pi}\left[-\frac{1}{2}\cos 2nx' \right]_{-\pi}^{\pi}\\\\ &=& 0\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8e5b1b10f61b61ce09798fdb67e5885f_l3.png)
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-L}^{L} \sin \frac{mx}{L} \cos \frac{nx}{L} \, dx &=& \int_{-\pi}^{\pi} \sin mx' \cos nx' \left(\frac{L}{\pi} \,dx'\right)\\\\ &=& \frac{L}{\pi}\int_{-\pi}^{\pi}\frac{1}{2}\left[ \sin(m+n)x'+\sin(m-n)x' \right] \, dx\\\\ &=& \frac{L}{2\pi}\left[-\frac{\cos(m+n)x'}{m+n}-\frac{\cos(m-n)x'}{m-n}\right]_{-\pi}^{\pi}\\\\ &=& 0 \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8c4c32df4d117b0709848dfe5bc90af7_l3.png)
となる。
直交性2
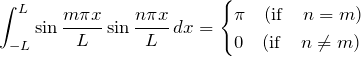
【証明】
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-L}^{L} \sin \frac{n\pi x}{L} \sin \frac{n\pi x}{L} \, dx &=& \int_{-\pi}^{\pi}\sin^2 nx' \,\left( \frac{L}{\pi} \,dx'\right)\\\\ &=& \frac{L}{\pi}\int_{-\pi}^{\pi}\frac{1-\cos 2nx'}{2} \,dx'\\\\ &=& \frac{L}{2\pi}\left[1-\frac{1}{2n}\sin 2nx' \right]_{-\pi}^{\pi}\\\\ &=& L \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-9684d2f1687eada3431c4ed01b6ea3df_l3.png)
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-L}^{L} \sin \frac{n\pi x}{L} \sin \frac{m\pi x}{L} \, dx &=& \int_{-\pi}^{\pi}\sin nx' \sin mx' \,\left( \frac{L}{\pi} \,dx'\right)\\\\ &=& \frac{L}{\pi}\int_{-\pi}^{\pi} \frac{1}{2}\left[ -\cos (m+n)x'+\cos (m-n) \right] \,dx\\\\ &=& \frac{L}{2\pi} \left[-\frac{\sin (m+n)x'}{m+n}+\frac{\sin (m-n)x'}{m-n} \right]_{-\pi}^{\pi}\\\\ &=& 0 \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-abba2468fe56f5bf1898685690435faf_l3.png)
となる。
直交性3
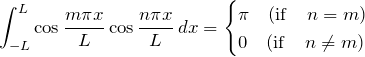
【証明】
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-L}^{L} \cos \frac{n\pi x}{L} \cos \frac{n\pi x}{L} \, dx &=& \int_{-\pi}^{\pi}\cos^2 nx' \,\left( \frac{L}{\pi} \,dx'\right)\\\\ &=& \frac{L}{\pi}\int_{-\pi}^{\pi}\frac{1+\cos 2nx'}{2} \,dx'\\\\ &=& \frac{L}{2\pi}\left[1+\frac{1}{2n}\sin 2nx' \right]_{-\pi}^{\pi}\\\\ &=& L \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4db5e3bd6493b377b084e3565b0cf64e_l3.png)
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-L}^{L} \cos \frac{n\pi x}{L} \cos \frac{m\pi x}{L} \, dx &=& \int_{-\pi}^{\pi}\cos nx' \cos mx' \,\left( \frac{L}{\pi} \,dx'\right)\\\\ &=& \frac{L}{\pi}\int_{-\pi}^{\pi} \frac{1}{2}\left[ \cos (m+n)x'+\cos (m-n)x' \right] \,dx'\\\\ &=& \frac{L}{2\pi} \left[\frac{\sin (m+n)x'}{m+n}+\frac{\sin (m-n)x'}{m-n} \right]_{-\pi}^{\pi}\\\\ &=& 0 \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a2b10ed2f62c5f83c8f040b6c273faba_l3.png)
となる。
場合分けに注意して計算すれば問題ないだろう。ちなみにこの問題は『青チャート』に載っているレベルの問題である。高校生は知らず知らずのうちに関数空間に迷い込んでいるのである。