フーリエ係数 ![]() は以下で求められるが、フーリエ係数の意味を簡単に説明しておこうと思う。以下で、
は以下で求められるが、フーリエ係数の意味を簡単に説明しておこうと思う。以下で、![]() は
は ![]() で周期的な関数とする。
で周期的な関数とする。
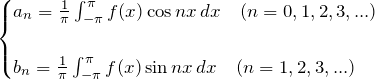
1. フーリエ係数の意味
フーリエ級数展開とは、周期 ![]() の周期関数
の周期関数 ![]() を同じ周期を持った三角関数で展開してやることである。こんな風に。
を同じ周期を持った三角関数で展開してやることである。こんな風に。
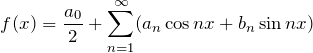
![]() は、
は、![]() がそれぞれの三角関数の成分をどれだけ持っているかを表す。
がそれぞれの三角関数の成分をどれだけ持っているかを表す。![]() は
は ![]() の重みを表す。
の重みを表す。
わかりやすいイメージ
初めてフーリエ級数になれていない人は、![]() によって身構えしてしまう。一回そのことは忘れよう。そして2次元の平面ベクトルに戻ってみてほしい。
によって身構えしてしまう。一回そのことは忘れよう。そして2次元の平面ベクトルに戻ってみてほしい。
下に平面ベクトル ![]() を用意した。見てわかる通り、
を用意した。見てわかる通り、![]() は
は ![]() 軸方向の成分である。そして、
軸方向の成分である。そして、![]() は
は ![]() 軸方向の成分である。
軸方向の成分である。
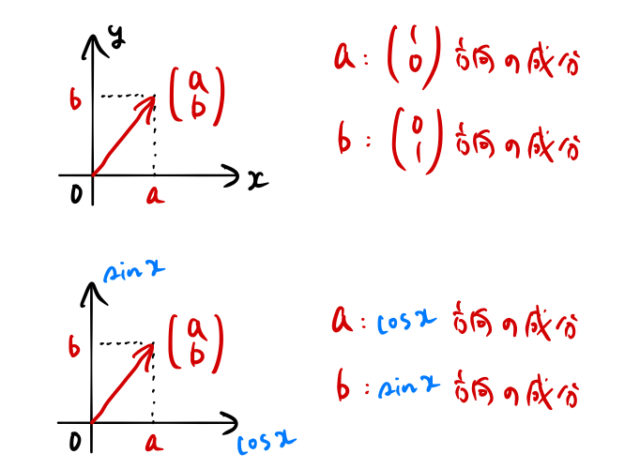
そして今まで ![]() 軸、
軸、![]() 軸と呼んでいたものを
軸と呼んでいたものを ![]() と
と ![]() に置き換えてしまったのが下の図である。フーリエ級数のイメージはこのようなものである。
に置き換えてしまったのが下の図である。フーリエ級数のイメージはこのようなものである。
結局 「![]() 方向の成分は何か?
方向の成分は何か?![]() 方向の成分は何か?」 を調べるのがフーリエ級数である。
方向の成分は何か?」 を調べるのがフーリエ級数である。
関数もベクトルと同じように扱うためには、とりあえずは下のように決めてやれば良い![]() 。
。
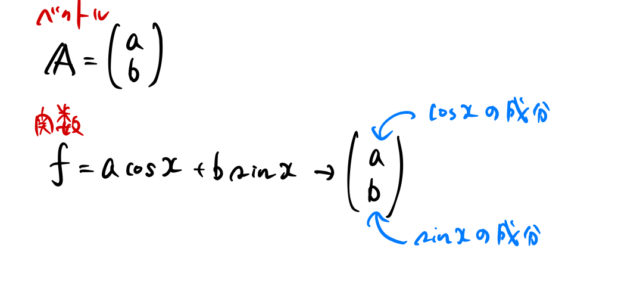
実際は、![]() であったため、ベクトルの次元は無限に大きい。
であったため、ベクトルの次元は無限に大きい。
フーリエ係数を求める
2次元ベクトルで ![]() の成分を求める場合は、求めたいベクトル
の成分を求める場合は、求めたいベクトル ![]() に対して、
に対して、![]() のベクトルで内積を取れば良い。そうすれば、図の上のように
のベクトルで内積を取れば良い。そうすれば、図の上のように ![]() が求められる。
が求められる。

![]() の場合も同様にできないだろうか?
の場合も同様にできないだろうか?
できる。ただし、![]() が直交する場合である。実はフーリエ級数は関数空間の話なので踏み込まないが、上のベクトルから拡張するためには以下に注意する。
が直交する場合である。実はフーリエ級数は関数空間の話なので踏み込まないが、上のベクトルから拡張するためには以下に注意する。
- 関数空間で「内積」を定義する
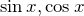 などが直交するか調べる
などが直交するか調べる
関数の内積の定義
ここでのフーリエ級数での二つの関数 ![]() の内積の定義は、
の内積の定義は、
![]()
ここでフーリエ級数においては
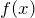 :フーリエ級数展開される側の関数
:フーリエ級数展開される側の関数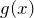 :
: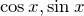 などの三角関数
などの三角関数
である。例えば、![]() とすると、
とすると、
![]()
となる。なんとなくフーリエ級数の形が見えてきたと思う。
三角関数の直交性
内積を定義すると、関数同士が直交しているかどうかわかる!
では、![]() の内積を計算してみる。
の内積を計算してみる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \sin x\cdot \cos x&=&\int_{-\pi}^{\pi} \sin x\cosx \, dx\\\\ &=&\frac{1}{2}\int_{-\pi}^{\pi}\sin 2x \,dx\\\\ &=&\frac{1}{2}\left[-\frac{1}{2}\cos 2x\right]_{-\pi}^{\pi}\\\\ &=& \textcolor{red}{0} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b5ad356cc5170f1866ae947e70d7337e_l3.png)
となり、![]() と
と ![]() は直交している!したがって、初めに見た絵のように座標軸が直交しているようなイメージになる。
は直交している!したがって、初めに見た絵のように座標軸が直交しているようなイメージになる。
自分自身との内積を考える。![]() として、
として、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \cos x\cdot \cos x&=&\int_{-\pi}^{\pi} \cos^2 x \, dx\\\\ &=&\frac{1}{2}\int_{-\pi}^{\pi} 1+\cos2x \,dx\\\\ &=&\frac{1}{2}\left[\frac{1}{2}\left(x+\sin 2x)\right]_{-\pi}^{\pi}\\\\ &=&\textcolor{red}{\pi}\neq 0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-39ea184fc1f1143dc6f2c39530c92443_l3.png)
となり直交していない。これは、![]() が関数空間である大きさ(ノルム)を持っているということである。
が関数空間である大きさ(ノルム)を持っているということである。
![]() などの一般的な三角関数についての内積は以下の通りである。
などの一般的な三角関数についての内積は以下の通りである。
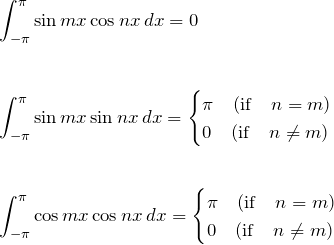
見ての通り、自分以外の関数とは直交することがわかる。したがって、初めにベクトルの成分を内積で取り出せたように、![]() のフーリエ係数
のフーリエ係数 ![]() を「関数の内積」で取り出せそうである。
を「関数の内積」で取り出せそうである。
ベクトル空間との違いは、
- 自分同士の内積は

- 内積の定義に注意する
である。
これを踏まえて以下ではフーリエ係数を導出する。
2. フーリエ係数の導出
以上の三角関数の直交性さえ理解していれば、フーリエ係数は簡単に導出できる。まず、周期 ![]() の
の ![]() を下のように展開する。
を下のように展開する。
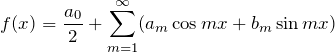
ここで、![]() と
と ![]() の内積をとる。つまり、両辺に
の内積をとる。つまり、両辺に ![]() をかけて
をかけて ![]() で積分する。
で積分する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\int_{-\pi}^{\pi} f(x)\cos nx \, dx\\\\ &&=\frac{a_0}{2} \int_{-\pi}^{\pi} \cos nx\, dx\\\\ &&+\sum_{m=1}^{\infty}\left[ a_m\textcolor{red}{\int_{-\pi}^{\pi} \cos nx \cos mx \, dx}+ b_m \textcolor{blue}{\int_{-\pi}^{\pi}\sin nx \cos mx \, dx} \right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-79c6bd7d94878465f755e865188d7e31_l3.png)
ここで、 ![]() の積分に関係のない
の積分に関係のない ![]() は
は ![]() の外に出した。
の外に出した。
右辺の積分で ![]() にならない部分がわかるだろうか?
にならない部分がわかるだろうか?
三角関数の直交性からもちろん ![]() の
の ![]() の部分だけが残る!そして自分同士の内積は
の部分だけが残る!そして自分同士の内積は ![]() であった。したがって、
であった。したがって、
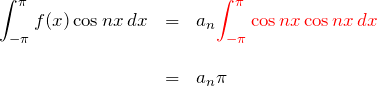
となり、
![]()
を得る。
![]() が欲しい場合は、
が欲しい場合は、![]() と
と ![]() の内積を取れば良い。つまり、
の内積を取れば良い。つまり、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-\pi}^{\pi} f(x)\, 1 \, dx&=&\frac{a_0}{2} \int_{-\pi}^{\pi} \, 1\, dx\\\\ &+&\sum_{m=1}^{\infty}\left[ a_m\int_{-\pi}^{\pi} \cos nx \, 1 \, dx + b_m \int_{-\pi}^{\pi}\sin nx \, 1 \, dx \right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-5cc86f9f0fe945b976cc32c1770269c8_l3.png)
より、
![]()
となる。![]() と置いているために、
と置いているために、![]() のときも下の形でまとめることができる。
のときも下の形でまとめることができる。
![]()
![]() を求める場合は、
を求める場合は、![]() と
と ![]() との内積を取れば良い。つまり、
との内積を取れば良い。つまり、![]() に
に ![]() をかけて
をかけて ![]() で積分すれば良い。結果は
で積分すれば良い。結果は
![]()
![]() がないのは、
がないのは、![]() だからである。
だからである。![]() のときは、
のときは、![]() の定数項として残っているだけである。
の定数項として残っているだけである。
3. まとめ
フーリエ係数は、三角関数の直交性から導出できることがわかっただろうか。また、平面ベクトルとの比較からフーリエ係数のイメージを持っておくと便利である。
![]() :基底ベクトルとして扱いやすくするためには、規格化しておくのが良いだろうが、ここでは単に
:基底ベクトルとして扱いやすくするためには、規格化しておくのが良いだろうが、ここでは単に ![]() を基底としてみている。
を基底としてみている。
最後の結果a_nとなっていますがb_nではないでしょうか.
修正いたしました。ありがとうございます。