大学の数学では線形空間なるものが現れます。高校で習うようなベクトルの空間をより一般化した概念ですが、ベクトル空間と同じように見ることで理解が深まります。線型空間の雰囲気だけでも味わえるように簡単な絵で説明していきます。
- 雰囲気を知ってもらうために「内積を定義する」ことはしなかった。
- 項目「2.3 フーリエ級数の例」以降は応用的な内容となっているため、難しかったらスキップしても良い。
1. ベクトル空間
関数空間の前にベクトルについて簡単に復習する。
1.1 基底
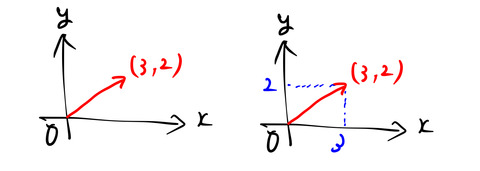
2次元の ![]() 平面を考える。
平面を考える。
例えば、![]() で表されるベクトルを考える。明らかに右の図のように
で表されるベクトルを考える。明らかに右の図のように ![]() 座標の値は 3 であり、
座標の値は 3 であり、![]() 座標の値は 2 である。このベクトルは下のように
座標の値は 2 である。このベクトルは下のように ![]() 軸方向に向いた単位ベクトル (1,0)と
軸方向に向いた単位ベクトル (1,0)と![]() 軸方向に向いた単位ベクトル (0,1) の2つで表すことができる。
軸方向に向いた単位ベクトル (0,1) の2つで表すことができる。
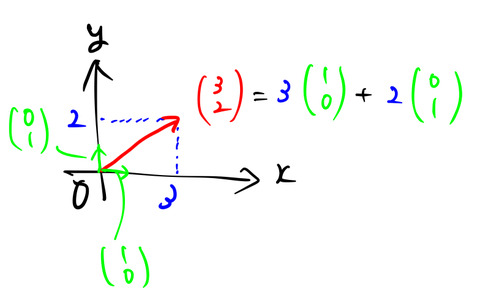
![]() 次元に拡張するためにベクトルを縦に書いている(縦ベクトル)。いま考えているベクトルは、
次元に拡張するためにベクトルを縦に書いている(縦ベクトル)。いま考えているベクトルは、
![]()
のように表すことができる。この軸を垂直にとった直交系における基底(緑色のベクトルに対応)は、
![]()
である。この2つの基底ベクトルにより、2次元平面に存在する任意のベクトルを表すことができる。
![]()
2次元平面はこれらの基底ベクトルによって”張られている”のである。基底ベクトルの取り方は一通りではない。例えば、
![]()
のような取り方もできるが、
![]()
のように表すことができ、これもまた基底である。2次元平面で平行でない2つのベクトルを基底にとることができる。その基底により、適当な係数で任意のベクトルを表すことができる。ただし、計算を簡単にするために、通常は以下の基底ベクトルを選択することが多い。
- 直交基底:基底ベクトルが互いに垂直である。
- 正規直交基底:すべての基底ベクトルの大きさが1(規格化された)で、互いに直交する。
1.2 3次元から 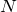 次元へ
次元へ
3次元の場合も同様に考えることができる。注意すべきは、任意のベクトルの成分は3つあるということである。したがって、基底は3つ必要である。よくある正規直交基底は、
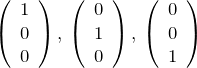
である。任意の3次元ベクトルはこの基底を用いて表すことができる(線型結合)。
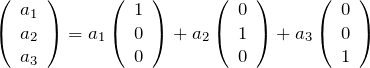
2次元の場合同様に、3次元も別の基底を用意することができる。正規直交化基底のひとつの例として、
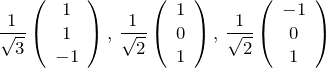
などがある。
![]() 次元空間への拡張も簡単である。
次元空間への拡張も簡単である。
![]() 次元ベクトルは
次元ベクトルは ![]() 個の成分をもつので、
個の成分をもつので、 ![]() 個の基底が必要である。
個の基底が必要である。
![]() 次元の正規直交基底のひとつは以下のように取れる。
次元の正規直交基底のひとつは以下のように取れる。
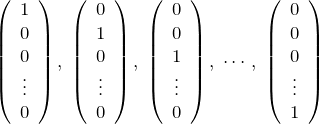
3次元と同じように
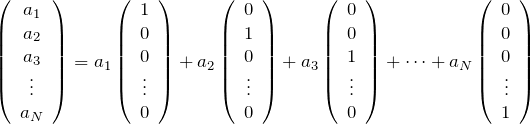
と表すことができる。
2. 関数空間
関数もベクトル空間と同じように扱おうとするのが関数空間である。
2.1 基底
例として、関数 ![]() を考える。この関数の係数を図のように並べてみる。
を考える。この関数の係数を図のように並べてみる。
これが関数空間である。簡単である。
基底の1行目が定数項、2行目が ![]() 、3行目が
、3行目が ![]() と表すというルールだけ課せば良い。そうすることで任意の関数はベクトル空間と同様の扱いが可能となる。
と表すというルールだけ課せば良い。そうすることで任意の関数はベクトル空間と同様の扱いが可能となる。
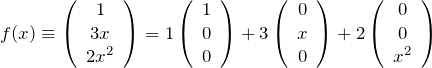
この場合の関数空間の次元は3であり基底は、
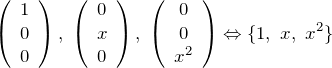
となる。右の表現の方が簡単に基底を表すことができる。別の基底の取り方もできる。例えば、
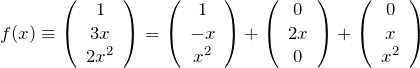
であるから、
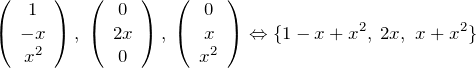
と基底を取ることもできる。
これが直交しているかは基底同士の内積を計算しないといけないが、ベクトル空間と同じような計算はできない。関数空間における内積を定義しないと計算できないが、ここでは省略する。
![]() 次元の拡張は容易にできるであろう。
次元の拡張は容易にできるであろう。![]() 個の基底を、
個の基底を、
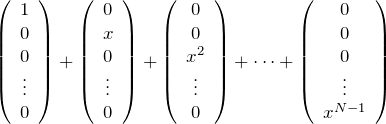
と取れば良い。
2.2 線型結合
2次元ベクトルの場合、2つの基底があれば任意の平面ベクトルは2つの基底を用いて表すことができると学んだ。![]() 次元ベクトルの場合も同様に
次元ベクトルの場合も同様に ![]() 個の基底を用いて表すことができる。このように基底を定数倍して足し合わせることで任意のベクトルを表現することを「線型結合」という。
個の基底を用いて表すことができる。このように基底を定数倍して足し合わせることで任意のベクトルを表現することを「線型結合」という。
関数空間の場合も同様に考えることができる。![]() 次元のベクトルについて
次元のベクトルについて
![]()
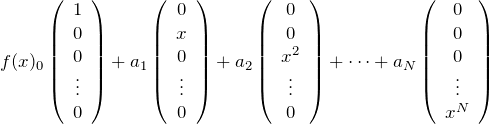
となり、基底 ![]() で任意の
で任意の![]() 次元の関数を線型結合で表すことができる。
次元の関数を線型結合で表すことができる。
2.3 フーリエ級数の例
フーリエ級数の例を考える。フーリエ級数は波がいろいろな波長を持っているときに、波長ごとの成分に分ける意味合いをもつ。
例えば、白色の光は、様々な色(波長)をもった波が重ね合わさって作られている。簡単に、赤、緑、青の光が1:1:1の割合で混ざって白色を作っているとしよう。
白色:![]()
赤色:![]()
緑色:![]()
青色:![]()
だとすれば、
![]()
いま、赤色、緑色、青色を組み合わせれば白色以外の色も作れる気がします。表現したい任意の色を ![]() だとすれば、それぞれの基底(色)の係数を
だとすれば、それぞれの基底(色)の係数を ![]() として、
として、
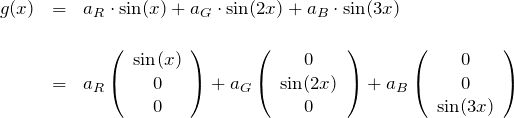
これを一般化するために 1と ![]() も含めて基底
も含めて基底
![]()
周期 ![]() の周期関数
の周期関数 ![]() は以下のようにフーリエ級数展開できる。
は以下のようにフーリエ級数展開できる。
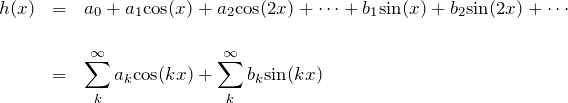
周期が ![]() の周期関数であれば、基底の周期も
の周期関数であれば、基底の周期も ![]() にした三角関数、
にした三角関数、
![]()
3. 状態空間
最後にもっと抽象的な空間を簡単に説明する。
3.1 量子力学に触れる
量子力学では状態が重ね合わせで表現されることがある。これは量子力学では測定前の状態はどちらの状態にもあるという事実を反映している。ここではこの「2つの状態が同時に存在する量子力学の不思議」については触れない。単に抽象空間である状態空間の、線型結合の例として考える。
状態ベクトルを ![]() (状態
(状態 ![]() )として
)として
-
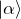 :状態1
:状態1 -
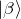 :状態2
:状態2
とする。このとき、状態 ![]() を状態1と状態2の
を状態1と状態2の ![]() と
と ![]() を係数として線型結合で表す。
を係数として線型結合で表す。
![]()
電子のスピンを考えよう。上向きと下向きのスピンがあったので、それを
-
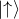 :電子が上向きスピンの状態
:電子が上向きスピンの状態 -
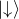 :電子が下向きスピンの状態
:電子が下向きスピンの状態
とする。このとき、ある電子の状態 ![]() (波動関数)は
(波動関数)は
![]()
量子力学の例では、具体的な基底の形を決めなかった。代わりに、抽象的な「状態」を基底にとることで、抽象的な波動関数を線型結合で表現することができた。この有用性は量子力学の内容であるため、ここでは説明しない。
とにかく、ベクトル空間・関数空間と同じように、量子力学の状態も基底を使って表しているということを知ってもらえれば十分である。
4 まとめ
この記事では、
ベクトル空間→関数空間→抽象空間
を簡単に説明した。それぞれの空間で内積を定義すれば、基底や線型結合の真髄を味わうことができるだろう。
お読みいただきありがとうございました。