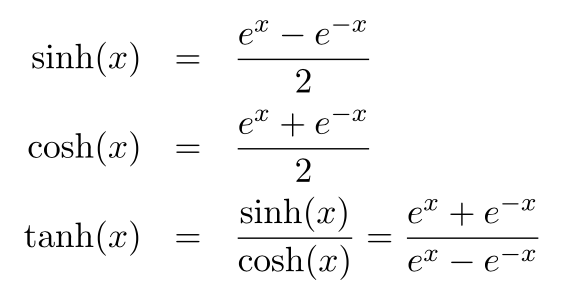全記事一覧 > 数学 > 微積分

【テイラー展開】双曲線関数tanh(x) （x~0）

　微分を学べば関数の展開が可能となる。ここでは、双曲線関数tanh(x)を展開していきたい(3次の項まで）。指数関数expのx=0におけるテイラー展開（マクローリン）を利用する方法を紹介する。

tanh(x)の x~0 における展開

    \begin{eqnarray*}{\rm tanh}(x)=x-\frac{1}{3}x^3 +O(x^5)\end{eqnarray*}

{\rm coth}(x)=\frac{1}{{\rm tanh}(x)} の展開は別にまとめた。

　　　

　　

1. exp(x)の展開による方法（ x~の展開)

\exp{(\pm x)} のマクローリン展開(x=0)を用いて整理する。

\exp{(\pm x)} の展開

    \begin{eqnarray*}\exp{(x)}=1+x+\frac{1}{2!}x^2 + \frac{1}{3!}x^3 +\frac{1}{4!}x^4+\cdots \\ \\\exp{(-x)}=1-x+\frac{1}{2!}x^2 - \frac{1}{3!}x^3 +\frac{1}{4!}x^4-\cdots\end{eqnarray*}

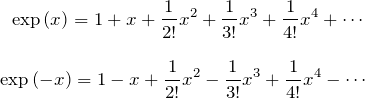
1.1 分子：exp(x)-exp(-x)の展開

    \begin{eqnarray*}\exp{(x)}-\exp{(-x)}&=&1+x+\frac{1}{2!}x^2 + \frac{1}{3!}x^3 +\frac{1}{4!}x^4+\cdots\\&-&\left(1-x+\frac{1}{2!}x^2 - \frac{1}{3!}x^3 +\frac{1}{4!}x^4-\cdots\right)\\ \\&\sim& 2\left( x + \frac{1}{6}x^3 + O(x^5) \right)\end{eqnarray*}

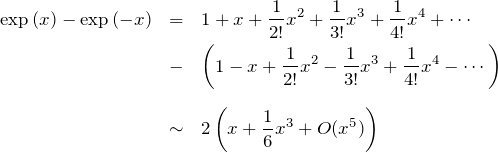
1.2 分母：exp(x)+exp(-x)の展開

    \begin{eqnarray*}\exp{(x)}+\exp{(-x)}&=&1+x+\frac{1}{2!}x^2 + \frac{1}{3!}x^3 +\frac{1}{4!}x^4+\cdots\\&+&\left(1-x+\frac{1}{2!}x^2 - \frac{1}{3!}x^3 +\frac{1}{4!}x^4-\cdots\right)\\ \\&=& 2\left( 1 + \frac{1}{2!}x^2 + \frac{1}{4!}x^4+\cdots \right)\\ \\&\sim& 2\left( 1 + \frac{1}{2}x^2 +O(x^4) \right)\end{eqnarray*}

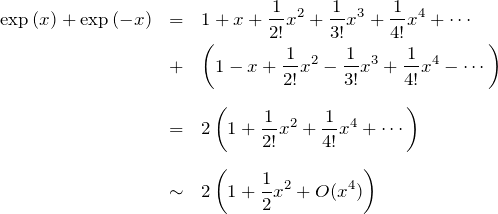
\frac{1}{1-x}=1+x+x^2+x^3+\cdots より、

    \begin{eqnarray*}\frac{1}{\exp{(x)}+\exp{(-x)}}&=&\frac{1}{ 2\left( 1 + \frac{1}{2!}x^2 +O(x^4) \right)}\\ \\&=&\frac{1}{2}\cdot \left( 1-\frac{1}{2}+O(x^4) \right)\end{eqnarray*}

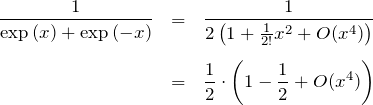
1.3 tanh(x)の展開(x~0)

    \begin{eqnarray*}{\rm tanh}(x)&=&\frac{\exp{(x)}-\exp{(-x)}}{\exp{(x)}+\exp{(-x)}}\\ \\&=& 2\left( x + \frac{1}{6}x^3 + O(x^5) \right) \cdot\frac{1}{2}\cdot \left( 1-\frac{1}{2}x^2+O(x^4) \right) \\&=& x +\frac{1}{6}x^3 -\frac{1}{2}x^3 + O(x^5) \\ \\&=& x-\frac{1}{3}x^3 +O(x^5)\end{eqnarray*}

{\rm tanh}xの x\sim0 における展開

    \begin{eqnarray*}{\rm tanh}(x)=x-\frac{1}{3}x^3 +O(x^5)\end{eqnarray*}

　

　

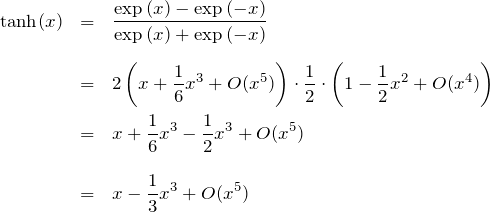
2. まとめ

　簡単に計算できる。


コメントを残す

メールアドレスが公開されることはありません。