以下のプランク(Planck)分布関数を導出・計算していく。
![]()
![]() は逆温度、
は逆温度、![]() はボルツマン定数で、
はボルツマン定数で、![]() は調和振動子の周波数である(
は調和振動子の周波数である(![]() でエネルギー単位に)。
でエネルギー単位に)。
![]() は調和振動子の個数であり、その平均値はプランク分布関数で表されていることを意味している。 導出過程の途中式は省略せずに書いたので、全員が導出できるはずである(もしできなかったら、完全にこちらの責任)。
は調和振動子の個数であり、その平均値はプランク分布関数で表されていることを意味している。 導出過程の途中式は省略せずに書いたので、全員が導出できるはずである(もしできなかったら、完全にこちらの責任)。
予備知識
導出にあたって最低限の予備知識をまとめておく。 以下で ![]() である。
である。
調和振動子のエネルギー
調和振動子のエネルギーは
![]()
で表される。 ざっくり言ってバネの振動を思い浮かべれば良いが、ここでは波(振動子)を粒子として扱い、![]() 個の粒子があると見る。 また、
個の粒子があると見る。 また、![]() はゼロ点振動になっており、
はゼロ点振動になっており、![]() の状態でもエネルギーがゼロにならないことを表す。
の状態でもエネルギーがゼロにならないことを表す。
分配関数Z
分配関数の簡単な説明は『【分配関数】Zの意味など』 に書いた。分布関数を求める上でも重要なので確認しておきたい。
エネルギー ![]() にある状態(振動子が
にある状態(振動子が ![]() 個ある状態)をとりうる確率は
個ある状態)をとりうる確率は
![]()
に比例する。 これは状態の詳細(位置や速度の情報)が異なっても、エネルギーが同じであればその状態にある確率は同じであることを意味する。 ![]() は相対的な確率であるため、確率の和を1に規格化するという意味合いで分配関数
は相対的な確率であるため、確率の和を1に規格化するという意味合いで分配関数 ![]() を
を
![]()
とする![]() 。 これにより、エネルギー
。 これにより、エネルギー ![]() にある状態をとりうる確率は
にある状態をとりうる確率は
![]()
となる。
*もう少し統計力学の意味で ![]() を考える必要もあるが、ここでは省略する。熱力学量との関連などについては別にまとめていきたい。
を考える必要もあるが、ここでは省略する。熱力学量との関連などについては別にまとめていきたい。
プランク分布関数の導出・計算
振動子の個数を ![]() 個とすると
個とすると ![]() の期待値
の期待値 ![]() は、
は、
![]()
ここで、![]() は調和振動子のエネルギーで、
は調和振動子のエネルギーで、
![]()
である。
(*)の右辺を計算していく。 (![]() が分母と分子に現れるので、分母の
が分母と分子に現れるので、分母の ![]() を求める
を求める ![]() のほうは
のほうは ![]() の代わりに
の代わりに ![]() としている。混乱しなければ
としている。混乱しなければ ![]() でも良い。)
でも良い。)
![Rendered by QuickLaTeX.com \begin{eqnarray*} \sum_n nP(E_n) &=&\sum_n \frac{n \exp(-\beta E_n)}{Z}\\ &=&\frac{1}{\textcolor{red}{Z}}\sum_n n\exp(-\beta E_n)\\ &=&\frac{\sum_n n\exp(-\beta E_n)}{\textcolor{red}{\sum_m \exp(-\beta E_m)}}\\ &=&\frac{\sum_n n\exp\left(-\beta \left[n+\frac{1}{2}\right]\hbar \omega\right)}{\sum_m \exp\left(-\beta \left[m+\frac{1}{2}\right]\hbar \omega\right)}\\ &=&\frac{\cancel{\exp\left(\frac{1}{2}\hbar \omega\right)}\sum_n n\exp\left(-\beta n\hbar \omega\right)}{\cancel{\exp\left(\frac{1}{2}\hbar \omega\right)}\sum_m \exp\left(-\beta m\hbar \omega\right)}\\ &=& \frac{\sum_n n\exp(-n \beta \hbar \omega)}{\sum_m \exp(-m \beta \hbar \omega)}\quad(*)' \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-0b84952a2126f601809ede4f697866aa_l3.png)
最後の式を簡単にしていく。分子と分母の ![]() の中身の違いは
の中身の違いは ![]() の前に
の前に ![]() (
(![]() ) があるかないかの違いである。 ここで、分母の式を
) があるかないかの違いである。 ここで、分母の式を ![]() で微分してやると
で微分してやると ![]() (
(![]() ) があらわれることに注目する。 すなわち、余分な係数を調整して、
) があらわれることに注目する。 すなわち、余分な係数を調整して、
![Rendered by QuickLaTeX.com \begin{eqnarray*} -\frac{1}{\hbar \omega}\frac{\partial }{\partial \beta}\left[\sum_m \exp(-m \beta \hbar \omega)\right] &=&\sum_m m\exp(-m\beta \hbar \omega)\\ &=&\sum_n n\exp(-n\beta \hbar \omega) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ac13967c04fef5e3d452f798e432be8c_l3.png)
となることを利用する。 よって、分母を
![]()
とおけば式(*)’は
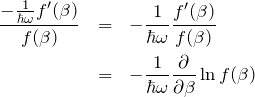
となる(この
結局、![]() ((*)’の分母)を簡単にして、自然対数をとり
((*)’の分母)を簡単にして、自然対数をとり![]() で微分すれば
で微分すれば ![]() を得ることがわかる。
を得ることがわかる。 ![]() は無限等比級数であるため、
は無限等比級数であるため、
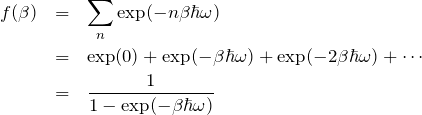
したがって、自然対数をとって微分すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} -\frac{1}{\hbar\omega}\frac{\partial }{\partial \beta }\ln \left[\textcolor{red}{\frac{1}{1-\exp(-\beta \hbar \omega)}}\right] &=&\frac{1}{\hbar\omega}\frac{\partial}{\partial \beta}\ln\left[ 1-\exp(-\beta \hbar \omega) \right]\\ &=&\frac{1}{\cancel{\hbar\omega}}\frac{-(-\cancel{\hbar \omega})\exp(-\beta \hbar \omega)}{1-\exp(-\beta \hbar \omega)}\\ &=&\frac{\exp(-\beta \hbar \omega)}{1-\exp(-\beta \hbar \omega)}\\ &=&\frac{1}{\exp(\textcolor{red}{+}\beta \hbar \omega)-1}\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-6291e20e153162cf2dc0c8b178c26b00_l3.png)
となる。最後の行への変形では、分母・分子に ![]() をかけている。
をかけている。
格子振動や光波などのエネルギーは、調和振動子の ![]() で量子化されたエネルギー
で量子化されたエネルギー ![]() で表すことができる。 したがって、格子振動を量子化したフォノンの数
で表すことができる。 したがって、格子振動を量子化したフォノンの数 ![]() はプランク分布関数
はプランク分布関数 ![]() にしたがう。 フォノンの個数の平均値がわかれば、それからフォノンのエネルギーの期待値
にしたがう。 フォノンの個数の平均値がわかれば、それからフォノンのエネルギーの期待値 ![]() などを計算することができ、格子振動の比熱なども計算できるようになる。
などを計算することができ、格子振動の比熱なども計算できるようになる。