全記事一覧 > 数学 > フーリエ変換／ラプラス変換

【フーリエ変換】デルタ関数・ガウス関数

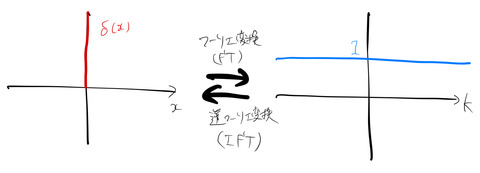
　よく知られているように、デルタ関数 \delta(x)は超関数である。

1. 定義


　上記のように通常の関数とは違い、定義としては

    \begin{eqnarray*}&\int_{-\infty}^{\infty}& \delta(x) f(x)dx = f(0) \\{\rm or} &\int_{-\infty}^{\infty}& \delta(x-x') f(x')dx' = f(x)\end{eqnarray*}

 
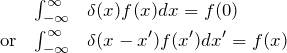
が用いられる。
　ここで、f(x)=e^{-ikx}とすれば、

    \begin{eqnarray*}&\int_{-\infty}^{\infty}& \delta(x) e^{-ikx}dx = e^{0}=1\end{eqnarray*}

 
となる。これは、デルタ関数のフーリエ変換が１になるというこである。大雑把に言ってしまえば、１の逆フーリエ変換はデルタ関数\delta(x)になる^{[1]}。

    \begin{eqnarray*}\frac{1}{2\pi}&\int_{-\infty}^{\infty}& 1\cdot e^{-ikx}dx = \delta(x)\end{eqnarray*}

 

　したがって、

    \begin{eqnarray*}2\pi \delta \leftrightarrow 1\end{eqnarray*}


のようなフーリエ変換の関係があるように思われる。絵で描いてみると下のようになる。

delta_Fourier

2. ガウス関数との関連

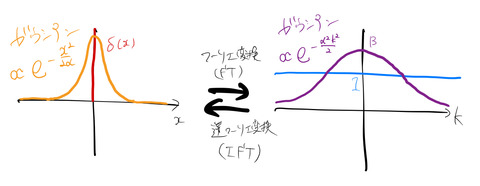
　補足的に、ガウス関数（ガウシアン）についてつけ加えるとの絵は下のようになる。

gaussian_Fourier

　ガウス関数(e^{\alpha x^2}型)のフーリエ変換に関する詳細な計算は「項目：ガウス関数で表された波動関数のフーリエ変換」でまとめた。左が実空間、右が逆空間（k空間）である。ガウス関数の指数部における\alphaはガウス関数の幅を表している。実空間（左図）で、幅が鋭い（\alphaの小さい）ガウス関数を与えれば、逆空間（右図）のガウス関数の幅は広がる。

　\alpha\rightarrow 0の極限は幅を無限に小さくする、すなわち、実空間のガウス関数をデルタ関数\delta(x)に近づけると、逆空間におけるガウス関数はの“1”に近くであろう。

　だから何？と思うかもしれないが、これは量子力学における不確定性原理を表している。運動量{\bf p}=\hbar {\bf k}は逆空間（{\bf k}空間）で与えられ、位置{\bf x}は実空間で与えられる。いま、ガウス関数の幅が不確定性を与える。つまり、位置{\bf x}が分かるということはガウス関数の幅を0にするということで、運動量{\bf p}=\hbar {\bf k}は無限の幅をもったガウス関数”１”となり、運動量を決めることができないのである。

デルタ関数およびガウス関数のフーリエ変換は、イメージとして覚えておくと実用的で便利である。

[1] これはフーリエ変換・逆フーリエ変換が可能かどうかを考えないで、進めているのでかなり乱暴である。それにもかかわらず、物理学などで現れるこの関係は非常に有益である。より数学的な扱いを求めるのであれば、他文献の参照をお願いしたい。


コメントを残す

メールアドレスが公開されることはありません。