波動関数を表現する関数は多い。ここでは代表的なガウス関数を用いた表現を学んでいきたい。![]() における波動関数
における波動関数![]() が、
が、
![]()
のようなガウス関数(ガウシアン)の形を取っているときのフーリエ変換を計算する。ここで、係数
1. フーリエ変換する
フーリエ変換 ![]() は、
は、
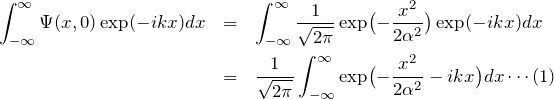
指数部分を
![Rendered by QuickLaTeX.com \begin{eqnarray*}-\frac{x^2}{2\alpha^2} -ikx &=&-\frac{1}{2\alpha^2}\bigl( x^2 + 2i\alpha^2 kx \bigr)\\&=&-\frac{1}{2\alpha^2}\Bigl[ (x+i\alpha^2 k)^2 + a^2 k^2 \Bigr]\\&=& -\frac{(x+i\alpha^2 k)^2}{2\alpha^2}-\frac{\alpha^2 k^2}{2}\\&=& -z^2 -\frac{\alpha^2 k^2}{2}\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-c00a5c5530f53d3f32372b9226133149_l3.png)
のようになる。最後の行では、
![]()
となる。積分区間は
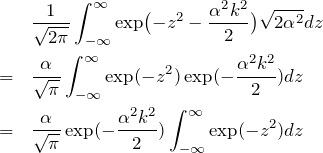
のように変形できる。最後の行では、
![]()
で与えられる。したがって、
![]()
で与えられる。この結果を見ると、