【積分】指数関数 exp(-ax^2) の積分（ガウス関数型）

　数学の微積分で頻繁に登場する、有名な指数関数の積分（ガウス関数、ガウシアン型）

$\begin{eqnarray*}&\int_{-\infty}^{\infty}\exp(-\alpha z^2)dz\\&(\alpha >0)\end{eqnarray*}$

を計算する。極座標表示を使えば非常に簡単に計算出来るということを学べるだろう。

$\sqrt{\alpha}z=x$ と積分変数を変換すれば、

$\begin{eqnarray*}\int_{-\infty}^{\infty}\exp(-az^2)dz&=&\int_{-\infty}^{\infty}\exp(-x^2) \frac{dx}{\sqrt{\alpha}}\\&=&\frac{1}{\sqrt{\alpha}}\int_{-\infty}^{\infty}\exp(-x^2) dx\end{eqnarray*}$

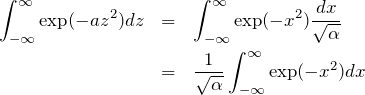
となるので、ここでは積分

$\begin{eqnarray*}I\equiv \int_{-\infty}^{\infty}\exp(-x^2)dx\end{eqnarray*}$

を計算しよう。

1. Iの2乗の計算

　積分は2つあるので、積分変数をそれぞれ $x$ と $y$ として、

$\begin{eqnarray*}I^2&=&\Bigl\{\int_{-\infty}^{\infty}\exp(-x^2)dx\Bigr\}\Bigl\{\int_{-\infty}^{\infty}\exp(-y^2)dy\Bigr\}\\&=&\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} \exp(-x^2)\exp(-y^2) dxdy\\&=&\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} \exp \Bigl[ -(x^2+y^2) \Bigr] dxdy\end{eqnarray*}$

の重積分を計算する。この重積分は極座標形式を用いると容易に計算できる。極座標表示は、

$\begin{eqnarray*}x&=&r{\rm cos}\theta\\y&=&r{\rm sin}\theta\\(r:0\rightarrow\infty&;& \theta: 0\rightarrow 2\pi)\end{eqnarray*}$

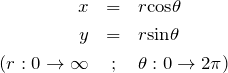
である。ここで、 $dxdy=rdrd\theta$ に注意して、

$\begin{eqnarray*}I^2 &=& \int_{0}^{2\pi} \int_{0}^{\infty} r\exp(-r^2) drd\theta\\&=& \int_{0}^{2\pi}d\theta \int_{0}^{\infty} r\exp(-r^2) dr\\&=& 2\pi \left[ -\frac{1}{2}\exp(-r^2) \right]_0^{\infty}\\&=& \pi\end{eqnarray*}$

である。両辺の平方根をとることにより $I=\sqrt{\pi}$ なので、

$\begin{eqnarray*}\int_{-\infty}^{\infty}\exp(-x^2)dx=\sqrt{\pi}\end{eqnarray*}$

となる。したがって、

$\begin{eqnarray*}\int_{-\infty}^{\infty}\exp(-\alpha z^2)dz=\sqrt{\frac{\pi}{\alpha}}\\\end{eqnarray*}$

を得る。

1. Iの2乗の計算

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル