全記事一覧 > 数学 > 微積分

絵でわかる「回転体の側面積（表面積）」の求め方

　回転体は微積分の応用的な位置づけにある。入試から試験までさまざまな場面で計算することが求められている。ここでは、関数 f(x) の回転体の側面積 S の求め方をまとめる。最終的な公式は以下の通りである。

    \begin{eqnarray*}S=\int_{a}^{b} 2\pi f(x) \sqrt{ 1+\{ f'(x)\}^2 } dx\end{eqnarray*}

 

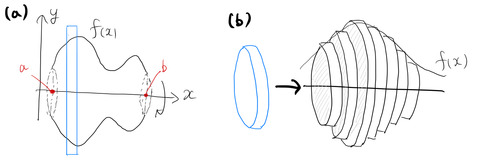
integral1

　図(a)のような関数を考えよう。基本的には、青色で囲まれた領域について考えて、それを足し合わせれば良い。図(b)は青色の領域について、f(x)の回転体を考えて、足し合わせた様子を表している。以下では、「いかに青色の回転体の側面積を求めるか」が問題となる。

1. 細かく区切ってみる

integral2

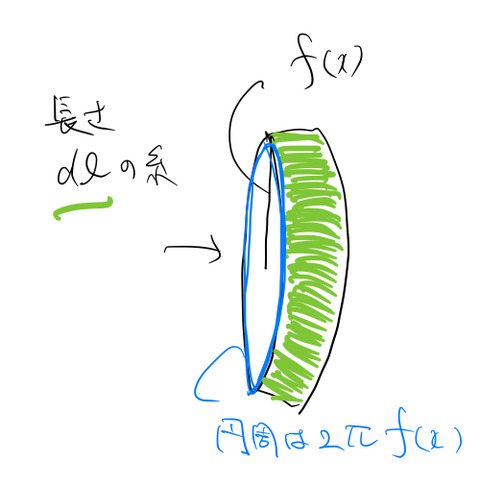
　図は青色の領域について回転する前の幾何学的な関係である。青色の回転体は円柱ではないので、dl で回転体の”高さ”を考える。この曲線の微小長さ dl は緑の直角三角形に対する三平方の定理より、

    \begin{eqnarray*}{dl}^2 &=& {dx}^2 + \{f'(x)dx\}^2 \\&=& \Bigl\{ 1 + \{f'(x)\}^2 \Bigr\} dx^2\\\therefore dl &=& \sqrt{ 1 + \{f'(x)\}^2 } dx\end{eqnarray*}

 
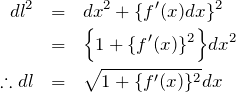
である。

2. 回転の様子

　青色の回転体の側面積 \Delta S は、下の図のようにこの緑色の”糸”を敷き詰めることで近似的に得られる。

integral3

 すなわち、近似的^{*}に側面積 \Delta S (x) は、

    \begin{eqnarray*}\Delta S(x) &=& 2\pi f(x) \times dl\\&=& 2\pi f(x) \sqrt{ 1 + \{f'(x)\}^2 } dx\end{eqnarray*}

 
となり、青色の回転体の側面積が求められた。求める f(x)の回転体の側面積 S は \Delta Sの積分によって求められる。

回転体の側面積

    \begin{eqnarray*} S=\int_{a}^{b} 2\pi f(x) \sqrt{ 1+\{ f'(x)\}^2 } dx \end{eqnarray*}

3. まとめ

このようにして回転体の側面積の公式を得る。
* 上記の方法はよく知られた直感的な導き方であるが、荒い部分もある。


コメントを残す

メールアドレスが公開されることはありません。