縮退のない場合の系で、演算子 ![]() と
と![]() に関して重要なことがある。
に関して重要なことがある。
演算子の交換関係 ![]()
![]() と
と![]() は同時固有状態を持つ
は同時固有状態を持つ
上の関係は、行列の交換関係と同時固有関数と読み替えてもよい。量子力学の場合は、関数よりも広い概念として同時固有状態と呼んでいる。
1. 証明
→方向と←方向について証明する。
1.1 同時固有関数→可換
演算子 ![]() と
と ![]() が同時固有関数をもつ。その固有関数を
が同時固有関数をもつ。その固有関数を ![]() 、固有値をそれぞれ
、固有値をそれぞれ ![]() 、
、![]() とする。つまり、以下のような関係にある。
とする。つまり、以下のような関係にある。
![]()
任意の波動関数 ![]() を
を![]() で展開すると、
で展開すると、
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}AB|\phi&=&\sum_i c_i \,AB\ket{a_i,b_i}\\&=&\sum_i c_i \,Ab_i\,\ket{a_i,b_i}\\&=&\sum_i c_i b_iA\ket{a_i,b_i}\\&=&\sum_i c_i b_i a_i\ket{a_i,b_i}\\ \\BA|\phi&=&\sum_i c_i \,BA\ket{a_i,b_i}\\&=&\sum_i c_i \,Ba_i\,\ket{a_i,b_i}\\&=&\sum_i c_i a_iB\ket{a_i,b_i}\\&=&\sum_i c_i a_i b_i\ket{a_i,b_i}\\&=&\sum_i c_i b_i a_i\ket{a_i,b_i}\\ \\\therefore [AB-BA]\ket{\phi}&=&(AB-BA)\ket{\phi}=0\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ad110472237b7cba13d31edd44d7795b_l3.png)
1.2 可換→同時固有関数
適当な基底を用意すると演算子は行列表示が可能となる。
![]()
となるような![]() の固有関数
の固有関数 ![]() を基底として考える。この基底で、
を基底として考える。この基底で、![]() と
と![]() を展開する。
を展開する。
演算子は適当な基底により行列表示が可能である。行列表示にすることで、計算が扱いやすくなる。
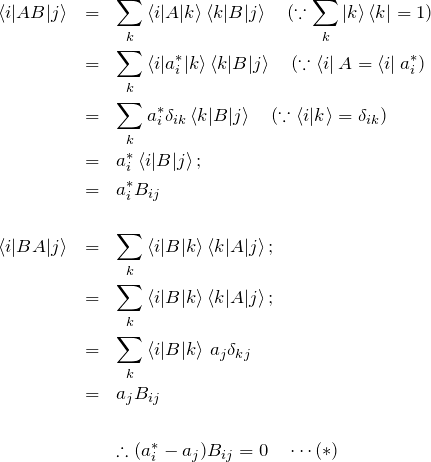
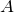 はエルミートである
はエルミートである  固有値は実数
固有値は実数- 縮退がない場合(異なる
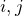 に対して
に対して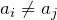 )
)
のときに(*)が成立するための条件は以下の通りである。
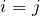 のとき、
のとき、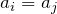 であるので(*)は成立する(
であるので(*)は成立する(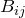 は0以外でも良い)
は0以外でも良い)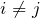 のとき、
のとき、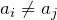 であるので、
であるので、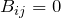
この条件を満たす ![]() は
は ![]() のとき以外は行列要素が0になった対角行列になっている。したがって、
のとき以外は行列要素が0になった対角行列になっている。したがって、![]() を対角化するように用意した固有関数
を対角化するように用意した固有関数 ![]() によって、
によって、![]() も対角化されていることが示された(同時対角化されている)。つまり、
も対角化されていることが示された(同時対角化されている)。つまり、![]() に対する
に対する![]() の固有値を
の固有値を ![]() とすれば、
とすれば、
(1) ![]()
である。 ![]() ,
,![]() の同時固有関数であることをはっきりさせるために
の同時固有関数であることをはっきりさせるために ![]() と書くこともある。
と書くこともある。
2. 同時固有関数(同時固有状態)を持つの意味
いつ同時固有状態が現れるのか、簡単に見ていこう。
2.1 例1:方位量子数と磁気量子数
量子力学にでてくる球面調和関数は、
方位量子数:![]()
磁気量子数:![]()
で表されているだろう。例えば状態は ![]() のように
のように![]() と
と![]() の値によって状態が指定されている。
の値によって状態が指定されている。![]() と
と ![]() という値が、上の証明で扱った固有値
という値が、上の証明で扱った固有値 ![]() 、
、![]() に対応している。
に対応している。
磁気量子数 ![]() とは何だっただろうか。その正体は、
とは何だっただろうか。その正体は、![]() 方向の
方向の![]() の値
の値 ![]() であった。そして、教科書に出てくるような交換関係を思い出して欲しい。
であった。そして、教科書に出てくるような交換関係を思い出して欲しい。
![]() となっていただろう。つまり、演算子
となっていただろう。つまり、演算子 ![]() と
と![]() に対して同時固有状態が存在するのである。また、これは
に対して同時固有状態が存在するのである。また、これは![]() のみでは状態を指定することができないことも表している。
のみでは状態を指定することができないことも表している。
![]() によって、演算子
によって、演算子 ![]() と
と![]() に対して同時固有状態が存在する。
に対して同時固有状態が存在する。
2.2 例2:ブロッホの定理
詳細な話は別の記事で書いたので参考にして欲しい。
固体物理における同時固有関数の例を見よう。シュレディンガー方程式、
![]()
の形は明らかに固有値方程式の形である。
結晶に周期性があり、ハミルトニアンの中にある ![]() が結晶格子と同じ並進対称性を持つ場合を考える。結晶格子の周期性に対応する格子ベクトル
が結晶格子と同じ並進対称性を持つ場合を考える。結晶格子の周期性に対応する格子ベクトル ![]() だけずらす並進移動の操作を
だけずらす並進移動の操作を ![]() とすると、
とすると、
![]()
が成立する。したがって、![]() と
と ![]() は同時固有関数をもつ。固有関数をシュレディンガー方程式を満たす上記の
は同時固有関数をもつ。固有関数をシュレディンガー方程式を満たす上記の ![]() とすれば、
とすれば、
![]()
![]()
となる。ここで、波数ベクトルを ![]() とした。
とした。
![]() によって、
によって、![]() と
と ![]() は同時固有関数をもつ
は同時固有関数をもつ
3. まとめ
意外とよく出でくる事項である。