微分方程式は物理学でよく現れる。たとえば、電磁気学ではポアソン方程式という形で現れたりする。一般解を求めることは、系の状態を決める上で重要である。
一般に、微分方程式の解き方はさまざまである。今回はラプラス変換を用いた解法を説明する。ラプラス変換による解法は知りたい関数 ![]() の初期状態
の初期状態 ![]() のときに強力である。ここでは、右辺がデルタ関数の場合の2階微分方程式を解いてみよう。
のときに強力である。ここでは、右辺がデルタ関数の場合の2階微分方程式を解いてみよう。
![]() で定義された実関数
で定義された実関数 ![]() に対する以下の2階微分方程式を解け。
に対する以下の2階微分方程式を解け。
(1) 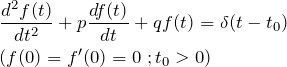
目次
1. ラプラス変換の復習
微分方程式を解く上で重要なラプラスの変換をざっくりと復習をしておこう。
1.1 exp(at)のラプラス変換(sシフト)
前提として、関数 ![]() が
が ![]() で定義されているということが重要である。これは、後にわかるように因果律と関係する。
で定義されているということが重要である。これは、後にわかるように因果律と関係する。
![]()
![]() のラプラス変換を計算する。
のラプラス変換を計算する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)={\mathcal L}[f(t)] &=& \int_{0}^{\infty} e^{at}\, e^{-st} \, dt\\ &=& \int_{0}^{\infty} e^{-(s-a)t} \, dt\\ &=& \left[ -\frac{1}{s-a}e^{-(s-a)t}\right]_0^{\infty}\\ &=& \frac{1}{s-a} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-463450ccee6aa1cf61bf361b64895a46_l3.png)
とにかく、ここでは収束する場合、![]() について計算した。つまり、指数関数が発散しない場合、
について計算した。つまり、指数関数が発散しない場合、![]() を考えている。
を考えている。
1.2 ずれた関数 f(t-t0) のラプラス変換(tシフト)
![]() のように、時間
のように、時間 ![]() から
から ![]() だけずれた場合のラプラス変換を求めておく。ただし、
だけずれた場合のラプラス変換を求めておく。ただし、![]() が
が ![]() 以上で定義されているため
以上で定義されているため
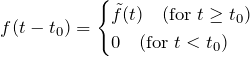
である。![]() はある関数を表す。
はある関数を表す。![]() のグラフは下図の通り。
のグラフは下図の通り。
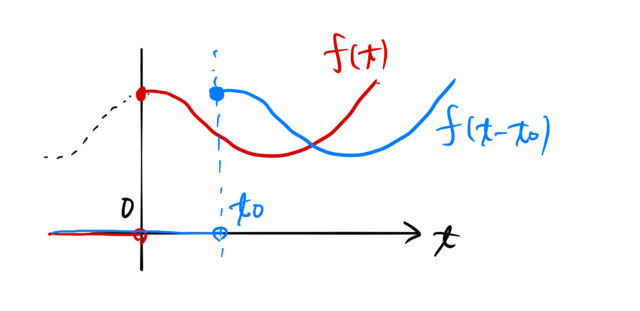
このとき、 ![]() のラプラス変換は
のラプラス変換は ![]() のとき
のとき ![]() である。また、
である。また、![]() のとき、
のとき、
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\mathcal L}[f(t-t_0)] &=& \int_{0}^{\infty} f(t-t_0)\, e^{-st} \, dt\\ &=& \int_{t_0}^{\infty} f(t')\, e^{-s(t'+t_0)} dt'\\ &=& \int_{\textcolor{red}{0}}^{\infty} f(t')\, e^{-s(t'+t_0)} dt' \quad(\because f(t)=0 ({\rm for}\; t \leq t_0)\\ &=& e^{-st_0} \int_{0}^{\infty} f(t')\, e^{-s(t')} dt'\\ &=& e^{-st_0} {\mathcal L}[f(t)] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a1377286400b3d02a31b6d96b99bc8b2_l3.png)
実関数が ![]() だけずれている場合は、ラプラス変換には
だけずれている場合は、ラプラス変換には ![]() の因子がつく。まとめると、
の因子がつく。まとめると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\mathcal L}[f(t-t_0)]= \begin{cases} e^{-st_0} {\mathcal L}[f(t)]\quad(t\geq t_0)\\\\ 0\quad(t<t_0) \end{cases}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-dab6a1c8de019063143890f36f85f371_l3.png)
1.3 導関数 f'(t), f”(t) のラプラス変換
![]() の導関数
の導関数 ![]() と
と ![]() をラプラス変換する。部分積分するだけで簡単に求められる。途中の定積分では、暗に
をラプラス変換する。部分積分するだけで簡単に求められる。途中の定積分では、暗に ![]() とした。(素直な
とした。(素直な ![]() を考えているという意味だが、ここでは深く立ち入らない。)
を考えているという意味だが、ここでは深く立ち入らない。)
![]() のラプラス変換:
のラプラス変換:
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\mathcal L}[f'(t)]&=& \int_{0}^{\infty} f'(t) e^{-st} \, dt\\ &=&[f(t) e^{-st}]_0^{\infty}- \int_{0}^{\infty} f(t) \left( \frac{d}{dt} e^{-st} \right) \, dt\\ &=& [0-f(0)] - (-s) \int_{0}^{\infty} f(t) e^{-st} \, dt\\ &=& -f(0)+s{\mathcal L}[f(t)] \quad \cdots (*) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-f890e94f300759b634f423c3fa84e300_l3.png)
![]() のラプラス変換:
のラプラス変換:
上の式(*) において、![]() ,
, ![]() とすればよい。
とすればよい。
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\mathcal L}[f''(t)]&=& -f'(0)+s{\mathcal L}[f'(t)]\\ &=& -f'(0)+s\left[ -f(0)+s{\mathcal L}[f(t)] \right] \quad (\because Eq.(*))\\ &=& -sf(0)-f'(0)+s^2 {\mathcal L}[f(t)] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-df1324067500b28a4cda4e394e4e9201_l3.png)
である。以下に結果をまとめておく。
![]()
1.4 デルタ関数 δ(t-t0) のラプラス変換
デルタ関数を定義しておく。
(2) ![]()
あるいは、
(3) ![]()
積分区間に注意して、![]() をラプラス変換する。
をラプラス変換する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\mathcal L}[\delta(t-t_0)]&=&\int_{0}^{\infty} \delta(t-t_0) e^{-st} \, dt\\ &=& \int_{-t_0}^{\infty} \delta(t') e^{-s(t'+t_0)} \, dt' \quad (t'\equiv t-t_0)\\ &=& \int_{-\infty}^{\textcolor{red}{\infty}} \delta(t') e^{-s(t'+t_0)}\,dt' \\ &=&e^{-st_0} \quad (\because Eq.(3)) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-05757f1de05a5b6b691f758af488971e_l3.png)
![]() と同じように、
と同じように、![]() の因子だけずれている。そして、
の因子だけずれている。そして、![]() に対して、
に対して、![]() であることがわかる。
であることがわかる。
2. 2階微分方程式を解く
例題を解く。
![]() で定義された実関数
で定義された実関数 ![]() に対する以下の2階微分方程式を解け。
に対する以下の2階微分方程式を解け。
(4) 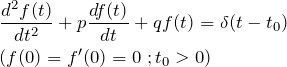
2.1 両辺をラプラス変換
左辺のラプラス変換 (![]() ):
):
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\mathcal L}[\frac{d^2 f(t)}{dt^2}]+ p{\mathcal L}[\frac{df(t)}{dt}]+ q{\mathcal L}[f(t)] &=& -sf(0)-f'(0)+s^2 F(s)\\ &+&p\left(-f(0)+sF(s)\right)\\&+& qF(s)\\\\ &=& s^2 F(s) + psF(s) qF(s)\\ \\ &=& [s^2 + ps + q]F(s) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-dc0b3c65c9fb9620028b7bd57fb1e0b4_l3.png)
右辺のラプラス変換:
(5) ![]()
したがって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} [s^2 + ps + q ]F(s) &=& e^{-st_0}\\ \\ F(s)&=& \frac{e^{-st_0}}{s^2+ps+q} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-2710919482a37b2eedacf49c3d36b7a5_l3.png)
たとえば、![]() と因数分解できるときは、部分分数分解を利用して、
と因数分解できるときは、部分分数分解を利用して、
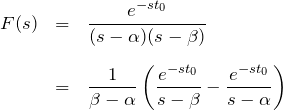
2.2 ラプラス逆変換する
はじめに、![]() のラプラス逆変換を考える。
のラプラス逆変換を考える。![]() は 1.2 で計算したように、
は 1.2 で計算したように、![]() のずらしたラプラス変換によってできることを思い出す。
のずらしたラプラス変換によってできることを思い出す。
するといまの場合は、![]() のラプラス変換
のラプラス変換 ![]() になっているものを探して、
になっているものを探して、![]() とずらせば良いことがわかる
とずらせば良いことがわかる ![]() となるのはすでに 1.1 で計算した、
となるのはすでに 1.1 で計算した、![]() の形である。
の形である。
ただし、![]() は
は ![]() が0以上のときに定義された関数で、0より小さいところでは0であるとする。したがって、
が0以上のときに定義された関数で、0より小さいところでは0であるとする。したがって、![]() において
において
![]()
であるため、![]() である。よって、求める逆変換 (
である。よって、求める逆変換 (![]() ) は、
) は、
![]()
である。同様に、
![]()
である。また、![]() ではラプラス逆変換は 0 である(1.2で見たように)。よって微分方程式の解は、
ではラプラス逆変換は 0 である(1.2で見たように)。よって微分方程式の解は、
 =\begin{cases} \frac{e^{\beta(t-t_0)}-e^{\alpha(t-t_0)}}{\beta-\alpha}\quad(t\leq t_0)\\\\ 0\quad(0\leq t<t_0) \end{cases}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a3ce74b9a8a3ae4c9c13f45725cd68b6_l3.png)
である。![]() が具体的な実数で与えられている場合は、2次方程式の解と係数の関係から計算すれば良い。つまり、
が具体的な実数で与えられている場合は、2次方程式の解と係数の関係から計算すれば良い。つまり、![]() であるため、
であるため、![]() である。
である。![]()
3. 補足:Green関数
なんとなく解いてきたがこの右辺がデルタ関数の微分方程式は、グリーン関数へとつながる。そのことについて簡単に触れておく。まず、式(4)の左辺を演算子 ![]() で表してみる。後にわかるように微分方程式の解
で表してみる。後にわかるように微分方程式の解 ![]() がGreen関数であるので、
がGreen関数であるので、![]() ,
, ![]() としておく。
としておく。
(6) ![]()
この解 ![]() は上で解いてきたような方法で具体的に求められる。ここで、同じ演算子
は上で解いてきたような方法で具体的に求められる。ここで、同じ演算子 ![]() に関する別の微分方程式を考えよう。
に関する別の微分方程式を考えよう。
(7) ![]()
この微分方程式の一般解 ![]() はGreen関数
はGreen関数 ![]() を用いて表すことができる。
を用いて表すことができる。
(8) ![]()
実際に(8)に代入して計算してみる。演算子 ![]() が
が ![]() に関する微分のみで、
に関する微分のみで、![]() に関する演算を含まないことに注意する。
に関する演算を含まないことに注意する。
(9) 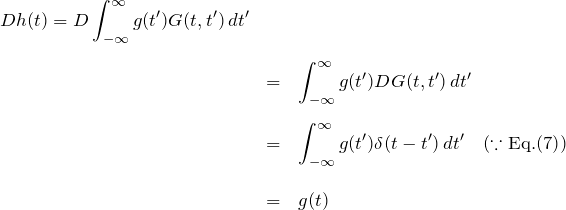
となり、確かに微分方程式の解であることが確認できる。
詳細については述べないが概要だけ述べておく。与えられた微分方程式(8)に対して、右辺にデルタ関数を含む微分方程式(7)を立てる。新しく立てた微分方程式の解である Green関数 ![]() を求めることで、もともとの微分方程式(8)を解いたことになる。これがGreen関数を用いた微分方程式の解法である。
を求めることで、もともとの微分方程式(8)を解いたことになる。これがGreen関数を用いた微分方程式の解法である。
4. まとめ
ラプラス変換を用いて微分方程式を解いてきた。丁寧に積分計算ができればラプラス変換は問題ない。また、逆変換については、もともとの形を思い浮かべたりしないといけないので慣れが必要である。
最後に、この例題では右辺がデルタ関数であるGreen関数に関する微分方程式と同じ形をしていることからGreen関数法について軽く触れた。Green関数については別で詳しくご紹介する予定である。