微分演算子であるルジャンドリアン![]() の固有値問題である
の固有値問題である
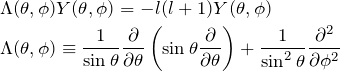
を解いて、固有関数を求めていく。ここで固有値は ![]() としている。 あとにわかるように、この固有関数
としている。 あとにわかるように、この固有関数 ![]() は球面調和関数になっている。
は球面調和関数になっている。
目次
導入
かんたんな導入をおこなう。
なぜ -l(l+1) と置くか?
一般的に演算子 ![]() に対する固有値方程式は
に対する固有値方程式は
![]()
![]() の固有値を
の固有値を ![]() と置くのは、
と置くのは、![]() に対する固有値問題を解く時に、ルジャンドルの微分方程式の形が現れるようにするためである。
に対する固有値問題を解く時に、ルジャンドルの微分方程式の形が現れるようにするためである。
ルジャンドルの微分方程式/ルジャンドル多項式
ルジャンドルの微分方程式について簡単に書いておく。微分方程式の形は
![]()
である。
【微分方程式】ルジャンドル多項式の導出(ルジャンドルの微分方程式)
この方程式を満たす ![]() の一つに、以下のルジャンドル多項式がある。
の一つに、以下のルジャンドル多項式がある。
![Rendered by QuickLaTeX.com \begin{eqnarray*} P_l(x)\equiv y(x)&=& \sum_{k=0}^{k=\left[\frac{l}{2}\right]} (-1)^k \frac{(2l-2k)!}{2^l k! (l-k)!(l-2k)!}x^{l-2k}\\ &=& \frac{(2l)!}{2^l (l!)^2} \left\{ x^l - \frac{l(l-1)}{2(2l-1)}x^{l-2}+ \frac{l(l-1)(l-2)(l-3)}{2\cdot 4 \cdot (2l-1)(2l-3)}x^{l-4}\cdots\right\} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a44657b5c5ef12b8bac5dba19688a055_l3.png)
ここで、![]() は
は ![]() を超えない最大の整数を表す。 いくつかの項を書いておくと
を超えない最大の整数を表す。 いくつかの項を書いておくと
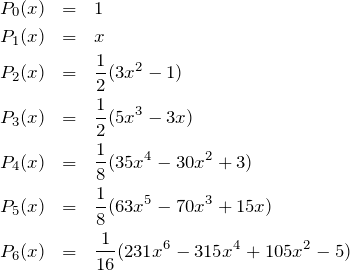
となる。
固有値・固有関数を求める
もう一度、解くべき式を書いておく。
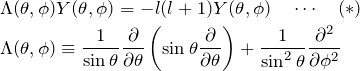
2変数関数を分離する
多変数関数の偏微分方程式を解く時の定石である、求める関数を複数の関数に分ける手法を用いる。
ここでは、![]() と
と ![]() を分離する。
を分離する。
![]()
と置き、式(*)に代入する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\frac{1}{\sin \theta}\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right) f(\theta)g(\phi)+\frac{1}{\sin ^2\theta}\frac{\partial^2}{\partial \phi^2}f(\theta)g(\phi)=-l(l+1)f(\theta)g(\phi)\\ \Leftrightarrow\quad &&\frac{\textcolor{blue}{g(\phi)}}{\sin \theta}\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right) f(\theta)+\frac{\textcolor{blue}{f(\theta)}}{\sin ^2\theta}\frac{\partial^2}{\partial \phi^2}g(\phi)=-l(l+1)\textcolor{blue}{f(\theta)g(\phi)}\\ \Leftrightarrow\quad &&\frac{1}{\textcolor{blue}{f(\theta)}\sin \theta}\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right) f(\theta)+\frac{1}{\textcolor{blue}{g(\phi)}\textcolor{red}{\sin ^2\theta}}\frac{\partial^2}{\partial \phi^2}g(\phi)=-l(l+1)\\ \Leftrightarrow\quad &&\left[\frac{\sin \theta}{\textcolor{blue}{f(\theta)}}\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+l(l+1)\sin ^2\theta\right] +\frac{1}{\textcolor{blue}{g(\phi)}}\frac{\partial^2}{\partial \phi^2}g(\phi)=0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-081e68bc703d84a6ace5fcf192af74de_l3.png)
ここでの計算の注意は以下のとおり。
- 2行目:微分に関係ない関数は左へ通り抜ける
- 3行目:両辺を
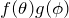 で割った
で割った - 4行目:両辺に
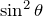 をかけた
をかけた
φについての関数を求める
最後の式の左辺は、
- 第一項[
 ]が
]が 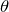 のみの関数
のみの関数 - 第二項が
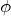 のみの関数
のみの関数
となっている。その和が0(右辺)なので、第一項と第二項はそれぞれ定数 ![]() である。
あとのため、定数を
である。
あとのため、定数を ![]() と置いた。
と置いた。
つまり、
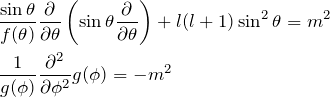
となる。2つ目の式から
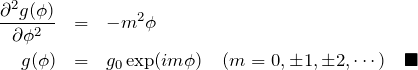
ここで物理的な観点から、周期性 ![]() を満たすため、
を満たすため、![]() は整数になる。 規格化定数
は整数になる。 規格化定数 ![]() は後で求める。
は後で求める。
θについての関数を求める
つぎに、![]() について、
について、
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\frac{\sin \theta}{f(\theta)}\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+l(l+1)\sin ^2\theta =m^2\\ \Leftrightarrow\quad &&\sin \theta\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+\left[l(l+1)\sin ^2\theta-m^2\right]f(\theta) =0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a417223a52ba5a1b1b7e1518af83cabb_l3.png)
ここで、![]() と置く。これは、極座標変換と同じである(図)。 また、
と置く。これは、極座標変換と同じである(図)。 また、![]() と置き換えておく。
と置き換えておく。
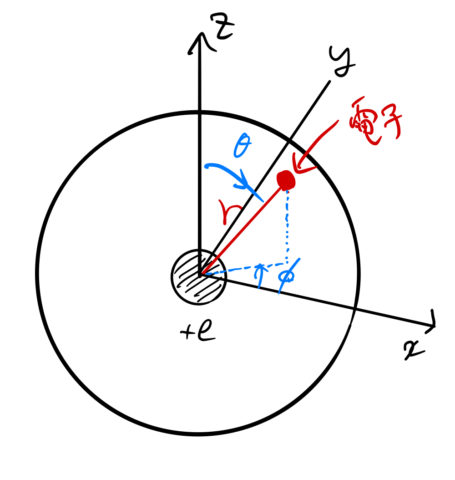
チェーンルールより
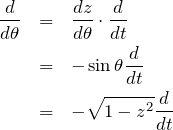
を利用する(また、1変数なので微分は ![]() としておく)。
としておく)。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\sqrt{1-z^2}\left( -\sqrt{1-z^2}\frac{d}{dz} \right)\left(-(1-z^2)\frac{d}{dz}\right)f(z) +\left[ l(l+1)(1-z^2) -m^2\right]f(z)=0\\ \Leftrightarrow\quad&& -(1-z^2)\frac{d}{dz}\left( -(1-z^2)\frac{df(z)}{dz} \right)+ \left[l(l+1)(1-z^2)-m^2\right]f(z)=0\\ \Leftrightarrow\quad&& \frac{d}{dz}\left[(1-z^2)\frac{df(z)}{dz}\right] -\left[l(l+1)-\frac{m^2}{1-z^2}\right]f(z)=0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ed79de7fdbd1ae222f206c343b5f0817_l3.png)
m=0のとき
![]() であったが、
であったが、![]() とすると、
とすると、
![]()
はルジャンドルの微分方程式そのものである。したがって、はじめに見たように
![Rendered by QuickLaTeX.com \begin{eqnarray*} f(z)=P_l(z)= \sum_{k=0}^{k=\left[\frac{l}{2}\right]} (-1)^k \frac{(2l-2k)!}{2^l k! (l-k)!(l-2k)!}x^{l-2k} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-080dc9917dffd140910c1d5520cad5b9_l3.png)
となる。最初に ![]() と固有値を決めておいたことで、ルジャンドルの微分方程式が現れたのである。
と固有値を決めておいたことで、ルジャンドルの微分方程式が現れたのである。
m≠0のとき
![]() のときはルジャンドルの微分方程式ではないが、その解はルジャンドルの陪多項式
のときはルジャンドルの微分方程式ではないが、その解はルジャンドルの陪多項式 ![]() になる。
このとき、微分方程式は
になる。
このとき、微分方程式は ![]() に依存していたため、多項式解が
に依存していたため、多項式解が ![]() に依存している。
また、
に依存している。
また、![]() については
については ![]() の形で微分方程式に現れているため、
の形で微分方程式に現れているため、![]() と表す。
と表す。
ルジャンドルの倍多項式 ![]() はルジャンドルの多項式
はルジャンドルの多項式 ![]() によって、
によって、
![]()
となることが知られている。![]() は
は ![]() を満たす
を満たす ![]() 個の整数であり、
個の整数であり、![]() に依存するため
に依存するため ![]() と書く。 この
と書く。 この ![]() は磁気量子数と呼ばれる。
は磁気量子数と呼ばれる。
以上より、![]() であったので、
であったので、![]() となる。
となる。
規格化定数
以上の結果をまとめて、
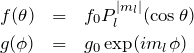
となる。次にそれぞれの規格化定数を求める。
![]() については簡単で、
については簡単で、
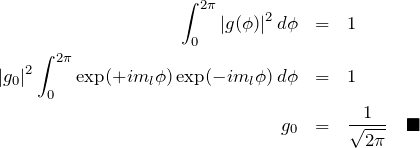
![]() については、極座標における
については、極座標における ![]() の積分に
の積分に ![]() が入ることに注意して、
が入ることに注意して、
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\int_0^{\pi} \left|f_0 P_l^{|m_l|}(\cos\theta)\right|^2\sin \theta d\theta=1\\ &&\int_{-1}^{1} \left|f_0 P_l^{|m_l|}(z)\right|^2\,dz=1\quad(\because z=\cos\theta)\\ &&|f_0|^2 \int_{-1}^{1} \left[P_l^{|m_l|}(z)\right]^2\,dz=1\\ \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ae1888c99000494a23f96fbe2ecb2dbe_l3.png)
となる。このルジャンドル陪多項式の規格化については煩雑なので結果のみを示す。
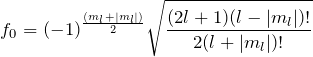
球面調和関数を得る
規格化定数を求めることができたので球面調和関数 ![]() を得る。
を得る。
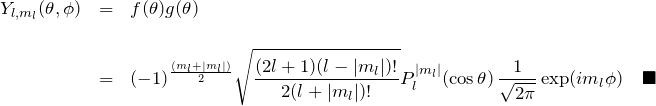
具体的な値は以下のとおり。
![]() :
:
![]()
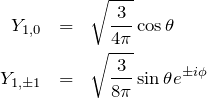
![]() :
:
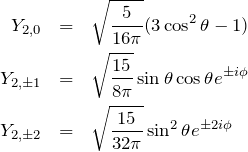
![]() :
:
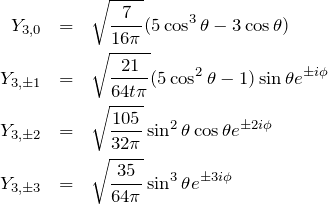
まとめ
![]() のときはルジャンドルの微分方程式(
のときはルジャンドルの微分方程式(![]() に依存しない)が現れ、その解がルジャンドル多項式
に依存しない)が現れ、その解がルジャンドル多項式 ![]() になる。
になる。 ![]() のときは
のときは ![]() に依存する微分方程式が現れ、その解がルジャンドル陪多項式
に依存する微分方程式が現れ、その解がルジャンドル陪多項式 ![]() になる。
になる。