フント則を使って![]() と
と![]() のイオンにおける電子配置を考える。自習用の穴埋め表と答えはこちら(pdf)。フント則の概要は以下の通り。
のイオンにおける電子配置を考える。自習用の穴埋め表と答えはこちら(pdf)。フント則の概要は以下の通り。
- Rule1:
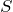 を最大にする(パウリの排他原理を満たして)
を最大にする(パウリの排他原理を満たして) - Rule2:
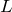 を最大にする(Rule1を満たして)
を最大にする(Rule1を満たして) - Rule3: 半閉殻以下(電子数が最大占有数の半分以下)のとき
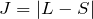 。半閉殻以上(電子数が最大占有数の半分以上)のとき
。半閉殻以上(電子数が最大占有数の半分以上)のとき 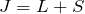
1. フント則(Rule1,2)
下図は、ルール1,2に従って ![]() 軌道と
軌道と ![]() 軌道に電子を配置したものである。
軌道に電子を配置したものである。
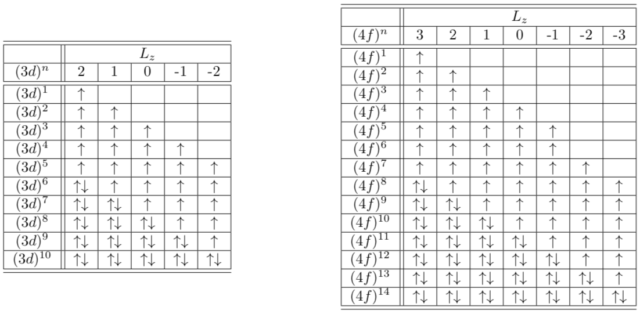
軌道の数は ![]() が5個、
が5個、![]() が7個である。したがって、それぞれに↑と↓スピンを詰めるので、最大で10個と14個の電子を配置することができる。
が7個である。したがって、それぞれに↑と↓スピンを詰めるので、最大で10個と14個の電子を配置することができる。
ルール1にしたがって、まず↑を半分まで(半閉殻)詰めていく。パウリの排他原理により同じ状態には↑を2つ詰めることはできない。![]() 軌道の場合は 6個目以降の電子は↓で詰めていく。
軌道の場合は 6個目以降の電子は↓で詰めていく。
ルール2では、![]() が最大となるように
が最大となるように ![]() の大きいものから電子を詰めていく。このフント則の2つのルールを満たすように電子を詰めていけば上の表のようになる。
の大きいものから電子を詰めていく。このフント則の2つのルールを満たすように電子を詰めていけば上の表のようになる。
2. ラッセル-サンダース記号
ラッセル-サンダース(Russell-Saunders)記号を導入する。全角運動量 ![]() を以下のように
を以下のように ![]() と
と ![]() で合成したものとする。
で合成したものとする。
![]()
このときに ![]() で区別できる項記号を導入する。
で区別できる項記号を導入する。
![]()
ここで ![]() については以下のスペクトル表記を用いて表す。
については以下のスペクトル表記を用いて表す。
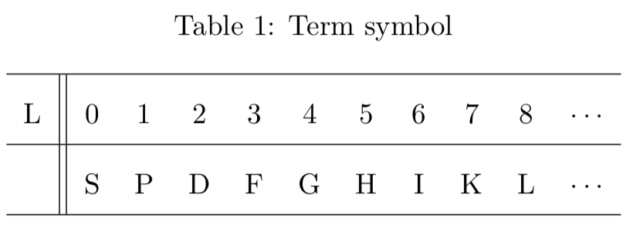
具体的な表記は後の表にまとめる。
3. 3d軌道(遷移金属)
以下に ![]() 遷移金属の ラッセル-サンダース記号,
遷移金属の ラッセル-サンダース記号, ![]() , ランデのg因子
, ランデのg因子 ![]() などをまとめた。
などをまとめた。
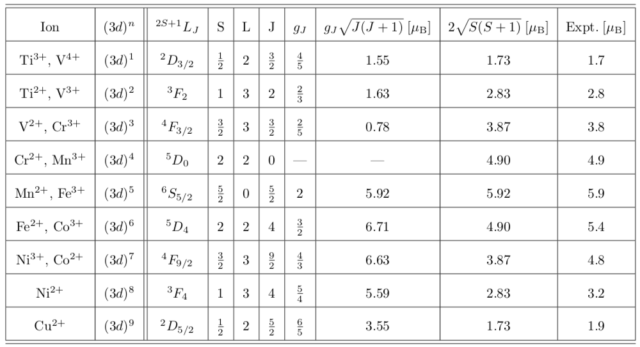
ここで、全角運動量 ![]() を
を ![]() で置き換えたモーメントが実験値とよく一致するのは
で置き換えたモーメントが実験値とよく一致するのは ![]() 電子の遍歴性により
電子の遍歴性により ![]() となるためである(軌道角運動量の消失(凍結))。次の
となるためである(軌道角運動量の消失(凍結))。次の ![]() との違いを覚えておく。
との違いを覚えておく。
4. 4f軌道(ランタノイド)
以下に ![]() 軌道をもったランタノイド(希土類元素の一部)のラッセル-サンダース記号,
軌道をもったランタノイド(希土類元素の一部)のラッセル-サンダース記号, ![]() , ランデのg因子
, ランデのg因子 ![]() などをまとめた。
などをまとめた。
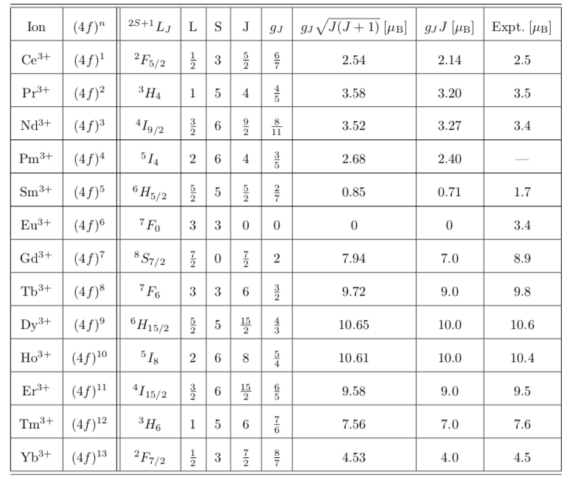
![]() 遷移金属との違いは全角運動量の値
遷移金属との違いは全角運動量の値 ![]() が良い量子数となっており、磁気モーメントが実験値とよく一致することである。 つまり、
が良い量子数となっており、磁気モーメントが実験値とよく一致することである。 つまり、![]() 軌道で起こったような角運動量の消失は起こりにくい。
軌道で起こったような角運動量の消失は起こりにくい。
この理由は、遷移金属とランタノイドの電子配置の違いによる。以下に ![]() の電子配置を示す(Cuなどの
の電子配置を示す(Cuなどの![]() になる特殊な場合を除く)。
になる特殊な場合を除く)。![]() は[Ar]核、
は[Ar]核、![]() は[Xe]核から書いた。
は[Xe]核から書いた。
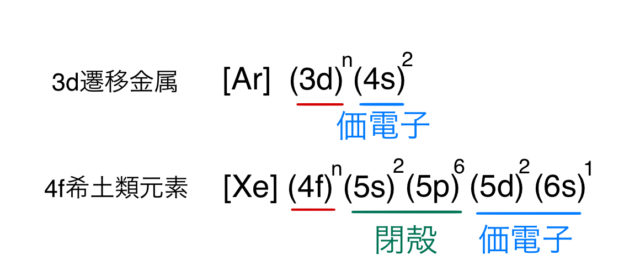
この配置から分かるように、![]() 軌道の外側には閉殻の
軌道の外側には閉殻の ![]() がある。陽イオンの価数としては、3つ価電子が取れて3価の陽イオンになる(例外としてEu
がある。陽イオンの価数としては、3つ価電子が取れて3価の陽イオンになる(例外としてEu![]() などがあるし、価数揺動もある)。
などがあるし、価数揺動もある)。
横軸に原子からの距離、縦軸に電子の存在確率をとると下図のようになる。
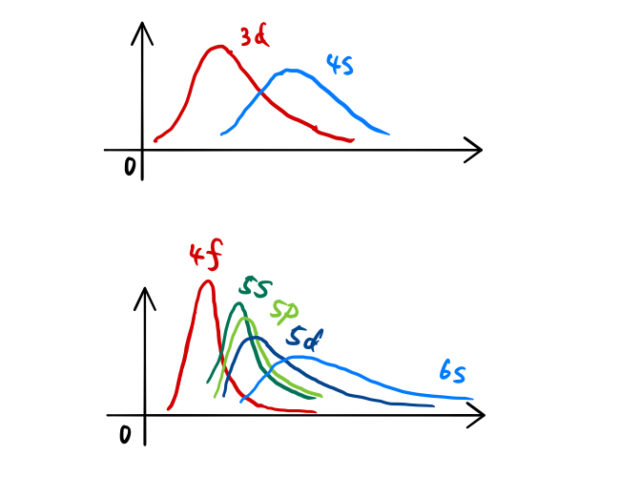
![]() 軌道の外側にある、電子の存在確率の大きい軌道は
軌道の外側にある、電子の存在確率の大きい軌道は ![]() 軌道のみである。このため、
軌道のみである。このため、![]() 軌道は結晶中を動き回ることもある(遍歴性)。そのような状況では、もはや孤立原子の中心対称ポテンシャルではない。結晶中のポテンシャルを受けて遍歴する電子は軌道角運動量はほとんど死んでいる(軌道角運動量の凍結)。
軌道は結晶中を動き回ることもある(遍歴性)。そのような状況では、もはや孤立原子の中心対称ポテンシャルではない。結晶中のポテンシャルを受けて遍歴する電子は軌道角運動量はほとんど死んでいる(軌道角運動量の凍結)。
一方で、![]() が価電子として抜けたとしても、
が価電子として抜けたとしても、![]() 軌道の外側に電子の存在確率の大きい
軌道の外側に電子の存在確率の大きい ![]() の閉殻が残る。この場合は、
の閉殻が残る。この場合は、![]() 軌道は原子の周りに局在した軌道となり、孤立原子の中心対称ポテンシャルと似た状況にある。したがって、合成した角運動量
軌道は原子の周りに局在した軌道となり、孤立原子の中心対称ポテンシャルと似た状況にある。したがって、合成した角運動量 ![]() は良い量子数になる。
は良い量子数になる。
5. まとめ
フント則で具体的に ![]() と
と ![]() の基底状態の電子配置を求めた。
の基底状態の電子配置を求めた。![]() の決定やラッセル-サンダース記号については練習問題としてよく問われるので習得しておきたい。
の決定やラッセル-サンダース記号については練習問題としてよく問われるので習得しておきたい。