水素原子などの球対称ポテンシャル ![]() をもったシュレディンガー方程式
をもったシュレディンガー方程式
![]()
を解くために、球面調和関数 ![]() を導入していく。
を導入していく。
ここでは ![]() と分離し、角度成分
と分離し、角度成分 ![]() に注目して見ていく。
に注目して見ていく。
球面調和関数の導入するところまで扱う。角運動量演算子との関係については次の項で扱う。
導入
われわれはシュレディンガー方程式を解くことで、電子の状態がわかる。 つまり電子の波動関数 ![]() を求めることが目的である。
を求めることが目的である。
極座標表示されたハミルトニアン
シュレディンガー方程式中のハミルトニアン ![]() は
は
![]()
![]()
球座標に変換する理由は、図のような水素原子などの系では球対称のポテンシャル ![]() を持つからである。
を持つからである。
つまり、電子の状態は原子からの距離 ![]() に依存する関数
に依存する関数 ![]() と角度
と角度 ![]() に依存する関数で表すことができる。
に依存する関数で表すことができる。
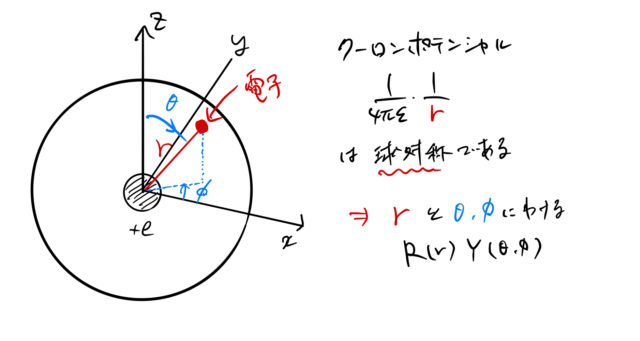
いまの場合、クーロンポテンシャルは原子と電子の距離 ![]() に反比例し、角度に依存しないため
に反比例し、角度に依存しないため ![]() のようになる。
のようになる。
また、![]() の極座標表示は、そこそこ量の計算のあと、
の極座標表示は、そこそこ量の計算のあと、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \nabla^2&=&\frac{1}{r^2}\frac{\partial }{\partial r}\left( r^2 \frac{\partial}{\partial r} \right)+\frac{1}{r^2}\Lambda(\theta,\phi)\\ &=&\frac{1}{r^2}\left[ \frac{\partial }{\partial r}\left( r^2 \frac{\partial}{\partial r} \right)+\Lambda(\theta,\phi)\right]\\ \Lambda(\theta,\phi)&=&\frac{1}{\sin \theta}\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right) +\frac{1}{\sin ^2\theta}\frac{\partial^2}{\partial \phi^2} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-3ddea0ed23b0dad2cfc03521e6f438ce_l3.png)
が導ける。![]() はルジャンドリアンと呼ばれる演算子で、角度
はルジャンドリアンと呼ばれる演算子で、角度 ![]() にのみ関係する。今回の主役である。
にのみ関係する。今回の主役である。
波動関数を距離と角度に分ける
水素原子のように球対称のポテンシャル
![]()
を持つ場合、電子の波動関数 ![]() は、原子からの
は、原子からの ![]() と角度成分
と角度成分 ![]() に分離できる。つまり、
に分離できる。つまり、
![]()
となる。
このような分離により、シュレディンガー方程式は微分方程式であるが、変数分離が使えそうである。
*ひとまず ![]() の添え字
の添え字 ![]() のことは忘れよう。
のことは忘れよう。
球面調和関数
球面調和関数を求めるときに ![]() は考えない。要するに角度成分
は考えない。要するに角度成分 ![]() のみを考えればよく、
のみを考えればよく、![]() は固定する。 半径
は固定する。 半径 ![]() の球殻上を電子が動いているイメージで良い。
の球殻上を電子が動いているイメージで良い。
* 動径 ![]() を変化させる場合は、動径関数
を変化させる場合は、動径関数 ![]() に関する微分方程式が得られ、その解はラゲール多項式によって表される。いまは触れない。角度だけ。
に関する微分方程式が得られ、その解はラゲール多項式によって表される。いまは触れない。角度だけ。
シュレディンガー方程式を解いていく
シュレディンガー方程式
![]()
に、極座標表示した ![]() 、分離した
、分離した ![]() を代入すると、
を代入すると、
![]()
となる。長い式であるが、![]() を固定して考えている今の場合、
を固定して考えている今の場合、![]() は定数として良い。 つまり、
は定数として良い。 つまり、
![]()
などはゼロとして進める(![]() の変化がないため、(
の変化がないため、(![]() の微分)
の微分)![]() (変化率)なのでゼロになる)。
(変化率)なのでゼロになる)。
結局、上の長い式は、
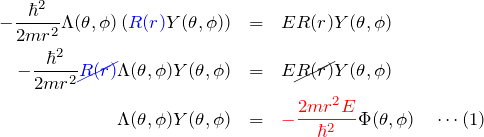
となる。ここで、![]() は
は ![]() に関係ないので、
に関係ないので、![]() は通り抜けている。
は通り抜けている。
ここで、ルジャンドリアン ![]() と球面調和関数
と球面調和関数 ![]() が
が
![]()
であることを用いる。この式は固有値方程式を表し、![]() の固有値が
の固有値が ![]() で、固有関数が
で、固有関数が ![]() であることを表している。 ここで
であることを表している。 ここで ![]() の制限は
の制限は ![]() 、
、![]() である。
である。
式(1)と式(2)を比べて、
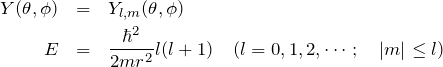
となる。したがって、エネルギー ![]() は
は ![]() によって量子化されている。
によって量子化されている。
球面調和関数の具体的な式
![]() の
の ![]() を書いておく。
を書いておく。 ![]() より
より ![]() は
は ![]() 個の値を取る。
個の値を取る。
![]() :
:
![]()
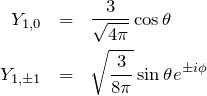
![]() :
:
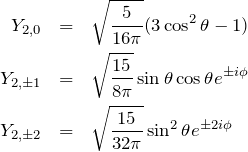
![]() :
:
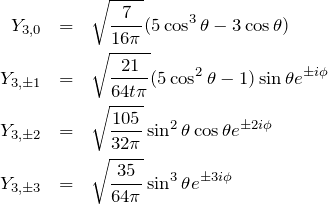
まとめ
とりあえず ![]() を固定して、角度成分に注目してシュレディンガー方程式を解いた。
を固定して、角度成分に注目してシュレディンガー方程式を解いた。
「解いた」といっても実際は、すでに知られているルジャンドリアンの固有関数である球面調和関数 ![]() を利用しただけであった。次回は球面調和関数と角運動量演算子との関わりを見ていく。
を利用しただけであった。次回は球面調和関数と角運動量演算子との関わりを見ていく。