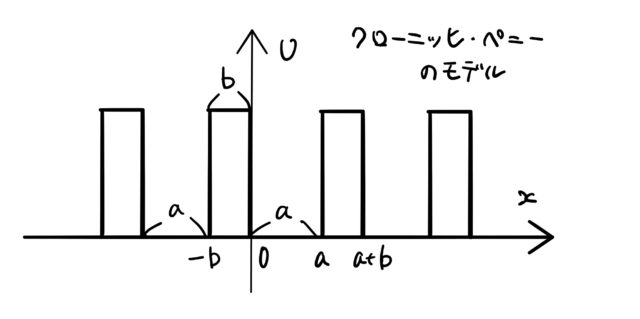
クローニッヒ・ペニー模型(Kronig-Penny model)では、図のような周期的な箱型ポテンシャルを仮定し、シュレディンガー方程式を解いていく。
無限・有限井戸型ポテンシャルの場合と異なって、結晶の周期性を反映した周期的なポテンシャル ![]() を用いるため、波動関数の形はブロッホ関数を仮定する。
を用いるため、波動関数の形はブロッホ関数を仮定する。
- 自由電子模型:無限に広い場合(3次元)
- 自由電子模型:端がない周期的な系(1次元、3次元)
- 1次元井戸型ポテンシャル(無限井戸)
- 1次元井戸型ポテンシャル(有限井戸)
- 周期ポテンシャルのある場合(ブロッホの定理)
- クローニッヒ・ペニー模型←
目次
ポテンシャルの設定とシュレディンガー方程式
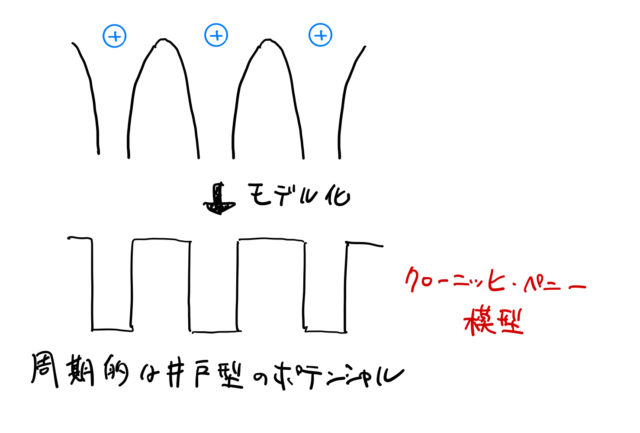
いま考えているポテンシャルの起源はクーロン力であるため、原子に近いほど電子は大きなポテンシャルを受け、谷のような形になる。 クローニッヒ・ペニー模型(モデル)では、このポテンシャルを単純化して、周期的な箱型ポテンシャルに置き換える。 箱型ではなく、cos型ポテンシャルで置き換える考え方もある。
いま、1次元の問題を考える。このとき、周期的な箱型ポテンシャル ![]() を図のように定める。
を図のように定める。
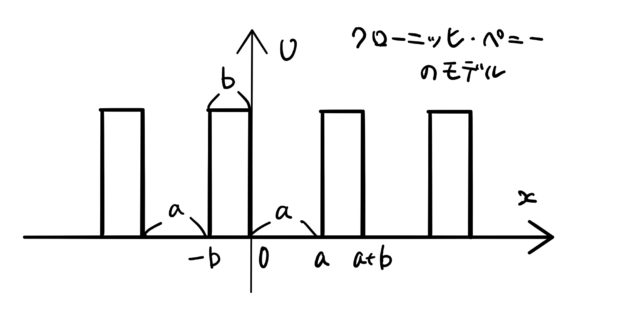
![]() の範囲で
の範囲で
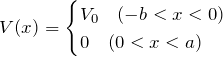
であり、![]() に対して周期的なポテンシャルになる(
に対して周期的なポテンシャルになる(![]() )。このとき、シュレディンガー方程式は
)。このとき、シュレディンガー方程式は
![]()
であり、これを解くことで波動関数 ![]() 、エネルギー固有値
、エネルギー固有値 ![]() を求めることができる。
を求めることができる。
ここで求める ![]() は
は ![]() の範囲における
の範囲における ![]() ではなく、全空間に対する
ではなく、全空間に対する ![]() である。 ただし、ポテンシャルに周期性があるためブロッホの定理より、
である。 ただし、ポテンシャルに周期性があるためブロッホの定理より、![]() の範囲の
の範囲の ![]() を求めるだけで十分である。なぜなら、これ以外の範囲については
を求めるだけで十分である。なぜなら、これ以外の範囲については
![]()
と書けるからである(ここで、![]() )。周期ポテンシャルの問題に関してはいつでもそうである。
)。周期ポテンシャルの問題に関してはいつでもそうである。
シュレディンガー方程式を解く
2つの領域に分けて、それぞれシュレディンガー方程式を解いていく。
領域:0<x<a の波動関数
この領域では ![]() であり、自由電子のときと同じように
であり、自由電子のときと同じように
![]()
であり、その解は平面波 ![]() (あるいは
(あるいは![]() )で表すことができる。ここで、
)で表すことができる。ここで、
![]()
である。 したがって、この領域では
![]()
である。![]() は定数。
は定数。
領域:-b<x<0 の波動関数
解くべきシュレディンガー方程式は
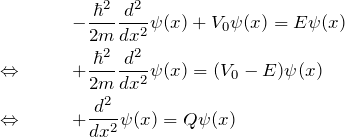
である。ここで、![]() に対応する量として
に対応する量として
![]()
と置いた(有限井戸の場合と同様)。 上の微分方程式の解の形は指数関数型になる。よって、
![]()
となる。
![]() が満たすべき条件を境界条件によって決定する必要がある。 このとき
が満たすべき条件を境界条件によって決定する必要がある。 このとき ![]() の境界において、
の境界において、![]() における
における ![]() が必要になるが、これは
が必要になるが、これは ![]() における
における ![]() にブロッホの定理を適用すれば良い。
にブロッホの定理を適用すれば良い。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\psi(x+L)=\psi(x)\exp(ikL)\quad(L=a+b)\\ \Rightarrow\quad &&\psi(a < x < a+b)=\psi(-b < x < 0)\exp(ik(a+b))\\ \Leftrightarrow\quad &&\psi(a < x < a+b)=\left[C\exp(Qx)+D\exp(-Qx)\right]\exp(ik(a+b)) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-0d701c53f8c7c9476a0e86be58b52291_l3.png)
これを用いることで、![]() における境界の波動関数が得られる。
における境界の波動関数が得られる。
境界条件
上で求めた波動関数をまとめると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \psi(x)=\begin{cases} C\exp(Qx)+D\exp(-Qx)\quad(-b < x < 0)\\ A\exp(iKx)+B\exp(-iKx)\quad(0 < x < a)\\ \left[C\exp(Qx)+D\exp(-Qx)\right]\exp(ik(a+b))\quad(a < x < a+b) \end{cases} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4c01cfa6d305c95317b6d3982385b7f3_l3.png)
である(![]() )。ここで、2つの境界
)。ここで、2つの境界 ![]() における波動関数
における波動関数 ![]() が連続かつ滑らかである条件を課す。
が連続かつ滑らかである条件を課す。
![]() の境界で、連続かつ滑らかである(微分係数が等しい)ことから
の境界で、連続かつ滑らかである(微分係数が等しい)ことから
![]()
となる。![]() においても同様に考える。
においても同様に考える。![]() と
と ![]() の関係より、
の関係より、
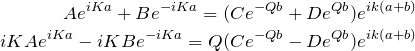
となる。![]() と
と ![]() が異なることに注意しながら、以上4つの条件から定数
が異なることに注意しながら、以上4つの条件から定数 ![]() を考える。自明な解以外の解を持つために、係数行列を作って行列式=0とすればよい(計算過程はこのページの最後にまとめた)。
を考える。自明な解以外の解を持つために、係数行列を作って行列式=0とすればよい(計算過程はこのページの最後にまとめた)。
最終的な結果を示すと
![]()
となる。
ポテンシャルを周期的なデルタ関数にする
方程式を作る
図のように ![]() の極限において、
の極限において、![]() が有限の値を持つために
が有限の値を持つために
![]()
から ![]() とする。このときポテンシャルは周期的なデルタ関数となる。
とする。このときポテンシャルは周期的なデルタ関数となる。

この極限では
![]()
である。また、![]() が有限の値
が有限の値 ![]() をとるとき、
をとるとき、
![]()
より、![]() である。
である。
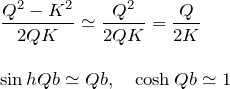
を用いて、式(1)を変形すると、
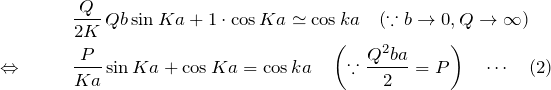
方程式の解と図示
この方程式が解を持つような ![]() の領域(横軸を
の領域(横軸を ![]() )を図示すると下のようになる。ここでは
)を図示すると下のようになる。ここでは ![]() の場合を考えている。説明のため、式(2)の左辺を
の場合を考えている。説明のため、式(2)の左辺を ![]() とする。左辺
とする。左辺 ![]() と右辺
と右辺 ![]() の交点が存在する時に方程式の解が存在する。いま右辺
の交点が存在する時に方程式の解が存在する。いま右辺 ![]() は-1から1までの値を取る(図の斜線部)。左辺の関数は図のオレンジの曲線で表した。
は-1から1までの値を取る(図の斜線部)。左辺の関数は図のオレンジの曲線で表した。
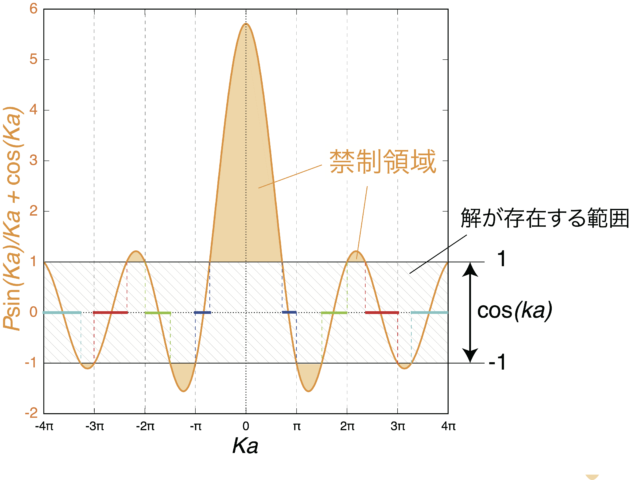
この図は情報が多いので丁寧めに説明していく。
![]() は
は ![]() を動かした範囲を図示しているが、
を動かした範囲を図示しているが、![]() を固定すると水平な直線になる。そのとき、
を固定すると水平な直線になる。そのとき、![]() (オレンジ)と交点を求めることができる。したがって、考えている
(オレンジ)と交点を求めることができる。したがって、考えている ![]() に対して
に対して ![]() を知ることができる。この
を知ることができる。この ![]() の値から
の値から
![]()
によって、エネルギー固有値 ![]() を求めることができる。また、図のように
を求めることができる。また、図のように ![]() は振動する関数であるため、
は振動する関数であるため、![]() との交点は複数個ある場合がある。
との交点は複数個ある場合がある。
逆に ![]() がある値のときには
がある値のときには ![]() となり、
となり、![]() との交点は存在しない。つまり、どんな
との交点は存在しない。つまり、どんな ![]() に対しても、「表現できない」
に対しても、「表現できない」![]() が存在する。
が存在する。![]() は
は ![]() に対応するため、ある特定のエネルギーを持つ状態が存在しないことがわかる。図では、オレンジで塗り潰した領域に対応し、禁制領域と呼ばれる。禁制領域によってエネルギー準位にギャップができることを後で説明する。
に対応するため、ある特定のエネルギーを持つ状態が存在しないことがわかる。図では、オレンジで塗り潰した領域に対応し、禁制領域と呼ばれる。禁制領域によってエネルギー準位にギャップができることを後で説明する。
以上のような禁制領域以外については状態が存在する。また、解の存在する領域上では連続的な ![]() (つまりエネルギー)を持ち、図では
(つまりエネルギー)を持ち、図では ![]() の小さいほうから「青、緑、赤、シアン」と色分けしている。この色分けた
の小さいほうから「青、緑、赤、シアン」と色分けしている。この色分けた ![]() (エネルギー)に対応して次の分散関係を説明する。
(エネルギー)に対応して次の分散関係を説明する。
得られた解と分散関係
![]() を変化させて
を変化させて ![]() を動かしたときの交点から
を動かしたときの交点から ![]() を求め、それからエネルギー
を求め、それからエネルギー ![]() を求めることができる。したがって、
を求めることができる。したがって、![]() の対応関係である分散関係
の対応関係である分散関係 ![]() を描くことができる。図に上の場合に対応する分散関係を示す(「青、緑、赤、シアン」と色分けは上の解に対応)。
を描くことができる。図に上の場合に対応する分散関係を示す(「青、緑、赤、シアン」と色分けは上の解に対応)。
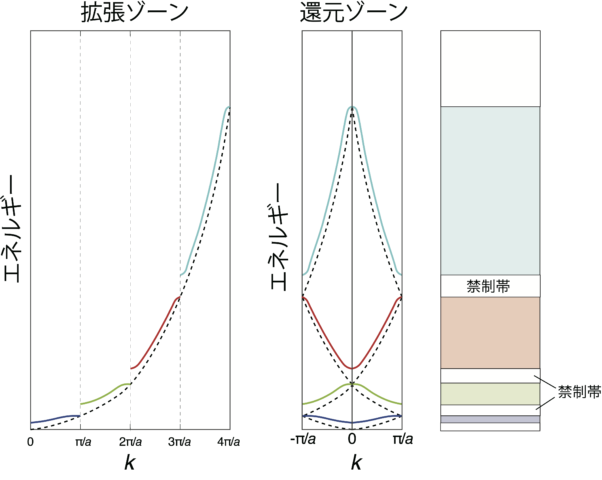
左は拡張ゾーンで、右は還元ゾーンである。還元ゾーンは、![]() を第一ブリルアンゾーン内(
を第一ブリルアンゾーン内(![]() )に折り返すことで得られる。
)に折り返すことで得られる。![]() の変化(
の変化(![]() )に対して、
)に対して、![]() は連続的に変化していたので分散関係も連続的になっている。
は連続的に変化していたので分散関係も連続的になっている。
ただし、禁制領域にある ![]() (エネルギー)をもつ解は存在しないため、分散関係にはエネルギーギャップができる。一番右の図にはそのバンド構造の概略図を示し、状態が存在できる領域(色塗り)と禁制帯の領域(白塗り)を描いた。
(エネルギー)をもつ解は存在しないため、分散関係にはエネルギーギャップができる。一番右の図にはそのバンド構造の概略図を示し、状態が存在できる領域(色塗り)と禁制帯の領域(白塗り)を描いた。
また、点線は自由電子の場合の分散関係
![]()
を描いている。自由電子の場合はブリルアンゾーンの端 ![]() にはギャップはない。クローニッヒペニー模型の場合、結晶中に周期ポテンシャルを導入することでギャップができている。このようなギャップの存在については、ほぼ自由な電子モデルの場合にも見られる。
にはギャップはない。クローニッヒペニー模型の場合、結晶中に周期ポテンシャルを導入することでギャップができている。このようなギャップの存在については、ほぼ自由な電子モデルの場合にも見られる。
(*) 行列式の計算過程
行列式の計算は好きなやり方で計算すればいいが、ここではその一例を示す。
途中の4つ連立方程式を ![]() に関する係数行列で表すことができる。
に関する係数行列で表すことができる。
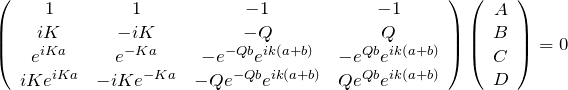
自明な解
係数行列を
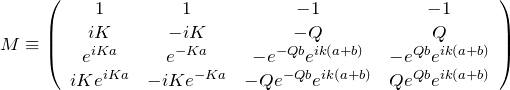
と置き、行列式
なる行列を用意する。この行列について
行列式の関係式
![]()
を用いると、
![]()
となる。したがって、以下では
下に計算の例を示す。等号についてのコメントを先に書いておく。
-
 行目:行列の積を計算し、
行目:行列の積を計算し、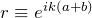 とおく
とおく
-
 行目:指数関数については
行目:指数関数については 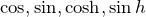 となってあらわれる。
となってあらわれる。
-
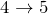 行目:(3列目)に(1列目)を加える
行目:(3列目)に(1列目)を加える
-
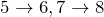 行目:赤色の成分についての余因子展開を利用
行目:赤色の成分についての余因子展開を利用
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&{\rm det}ML\\ &=&\left|\left(\begin{array}{cccc} 1 & 1 & -1 & -1\\ iK & -iK &-Q &Q\\ e^{iKa}& e^{-Ka} &-e^{-Qb}e^{ik(a+b)}&-e^{Qb}e^{ik(a+b)}\\ iKe^{iKa}& -iKe^{-Ka} &-Qe^{-Qb}e^{ik(a+b)}&Qe^{Qb}e^{ik(a+b)} \end{array}\right) \frac{1}{2}\left(\begin{array}{cccc} 1 & 1 & 0 & 0\\ 1 & -1 & 0 & 0\\ 0&0& 1 & 1\\ 0&0& 1 & -1 \end{array}\right) \right|\\ &=& \frac{1}{2}\left| \begin{array}{cccc} 2 & 0 & -2 &0\\ - & 2iK & 0 & -2e^{+Qb}\\ e^{+iKa}+e^{-iKa} & e^{+iKa}-e^{-iKa} &-r (e^{+Qb}+e^{-Qb}) & r(e^{+Qb}-e^{-Qb})\\ iK(e^{+iKa}-e^{-iKa}) & iK(e^{+iKa}+e^{-iKa}) & Qr(e^{+Qb}-e^{-Qb}) & -Qr(e^{+Qb}+e^{-Qb}) \end{array} \right|\\ &=& \left| \begin{array}{cccc} \textcolor{blue}{1} & 0 & \textcolor{blue}{-1} & 0\\ \textcolor{blue}{0} & iK & \textcolor{blue}{0} & -Q\\ \textcolor{blue}{\cos Ka} & i\sin Ka &\textcolor{blue}{- r \cosh Qb} & r\sinh Qb\\ \textcolor{blue}{-K\sin Ka} & iK\cos Ka &\textcolor{blue}{Qr \sinh Qb} & -Qr\cosh Qb \end{array} \right|\\ &=& \left| \begin{array}{cccc} \textcolor{red}{1}& 0 & 0 & 0\\ 0& iK & 0 & -Q\\ \cos Ka & i\sin Ka & \cos Ka - r\cosh Qb & r\sinh Qb\\ -K\sin Ka & iK \cos Ka & -K\sin Ka + Qr \sinh Qb & -Qr\cosh Qb\\ \end{array} \right|\\ &=& \left| \begin{array}{cccc} \textcolor{blue}{i}K & 0 & -Q\\ \textcolor{blue}{i}\sin Ka & \cos Ka - r\cosh Qb & r\sinh Qb\\ \textcolor{blue}{i}K \cos Ka & -K\sin Ka + Qr \sinh Qb & -Qr\cosh Qb\\ \end{array} \right|\\ &=& \textcolor{blue}{i}\left| \begin{array}{cccc} \textcolor{red}{K} & 0 & \textcolor{red}{-Q}\\ \sin Ka & \cos Ka - r\cosh Qb & r\sinh Qb\\ K \cos Ka & -K\sin Ka + Qr \sinh Qb & -Qr\cosh Qb \end{array} \right|\\ &=& i\textcolor{red}{K} \left| \begin{array}{cccc} \cos Ka - r\cosh Qb & r\sinh Qb\\ -K\sin Ka + Qr \sinh Qb & -Qr\cosh Qb \end{array} \right|\\ &&\quad +i \textcolor{red}{(-Q)} \left| \begin{array}{cccc} \sin Ka & \cos Ka - r\cosh Qb \\ K \cos Ka & -K\sin Ka + Qr \sinh Qb \end{array} \right|\\ &=& i\Biggl[ K\Bigl\{ \left(\cos Ka -r \cosh Qb\right)(-Qr\cosh Qb) -r \sinh Qb(-K\sin Ka + Qr\sinh Qb) \Bigr\}\\ &&\quad -Q \Bigr\{ \sin Ka\left( -K\sin Ka + Qr \sinh Qb\right) -K\cos K a\left( \cos Ka -r \cosh Qb\right) \Bigr\} \Biggr] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-1aba91fd04ecda59e5d6830ec6cadbfc_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&i[\,-KQr\cos Ka \cosh Qb + \textcolor{magenta}{KQr^2\cosh^2 Qb}\\ &&\quad\quad+K^2 r \sin Ka \sinh Qb \textcolor{magenta}{- KQr^2 \sinh^2 Qb}\\&&\quad\quad+\textcolor{blue}{KQ\sin ^2 Ka} - Q^2 r \sin Ka \sinh Qb\\&&\quad\quad+\textcolor{blue}{KQ\cos^2 Ka} - KQr\cos Ka \cosh Qb\,]\\\\ &=& iKQ\left\{r^2 -2r\cos Ka \cos Qb +r\left(\frac{K}{Q}-\frac{Q}{K}\right)\sin Ka \sinh Qb +1\right\}\\\\ &&\quad\quad\bigl(\,\because\, \textcolor{magenta}{\cosh^2 x - \sinh^2 x =1};\, \textcolor{blue}{\cos^2 x + \sin ^2 x=1}\bigr) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-17c43b6f76def8dab6f5ba357d6b3097_l3.png)
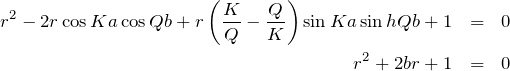
となる。ここで、
![]()
![]()
となる。
![]()
より実部を比較して
![]()
となる。