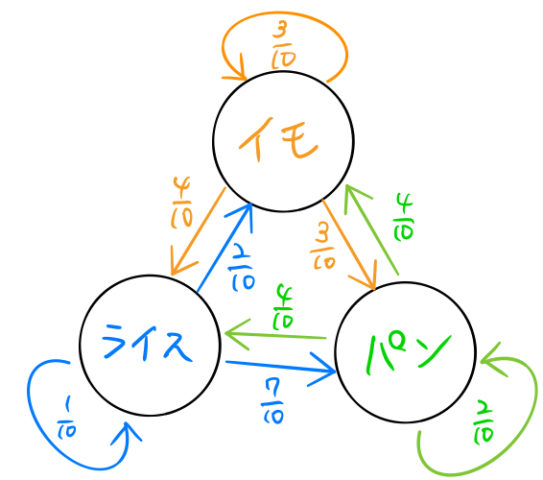
現在の状態が過去の状態によって確率的に決定されるというマルコフ過程(マルコフ連鎖)を説明するために簡単な例を用意した。昨日の朝食によって、今日の朝食が確率的に決まるような話である。見ていこう。
毎日朝食には「ライス」、「パン」、「イモ」のいずれかを食べる。昨日食べた朝食によって確率的に今日の朝食を決めるように執事に伝えている。朝食の確率的な決定(遷移)は上の絵のとおり行われる。一昨日の朝食が「ライス」であったときに、今日の朝食が「ライス」である確率を求めよ。
1. 行列で見る
マルコフ連鎖では行列を用いて状態の遷移を表現することがある。以下では、確率遷移行列を導入し、例題を解いてみる。
1.1 確率遷移行列をつくる
昨日の朝食によって確率的に今日の朝食が決まる時、遷移の様子を行列により表現することができる。状態は、「ライス」「パン」「イモ」の3通りであるため、3次元のベクトルで状態を表すことができる。以下の図にその様子を示した。
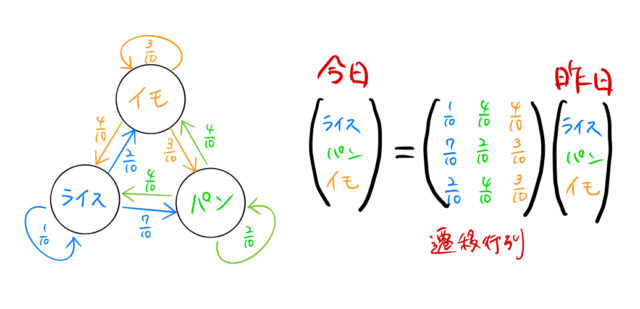
この図によれば、昨日の状態(ベクトル)を遷移行列でつなぐことにより今日の状態(ベクトル)を表現している。
同様にして、昨日の状態(ベクトル)も一昨日の状態(ベクトル)によって下のように表現できる。波線のところを再度、行列で表現すれば良い。
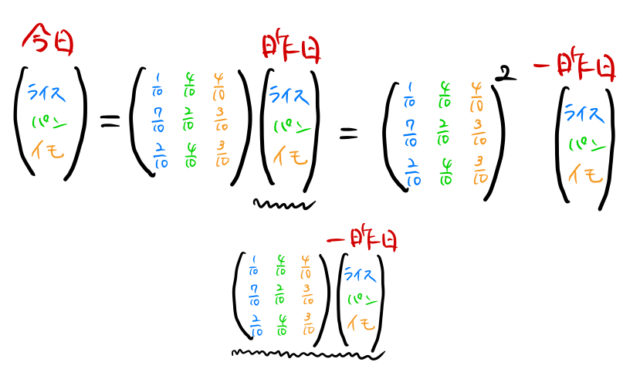
一昨日の朝食は「ライス」であったため、一昨日のベクトルについては「ライス」の成分が1で、残りの「パン」「イモ」は0である(ライス100%)。

1.2 確率遷移行列による解法
求めたい確率は左にあるベクトルの 今日の「ライス」 である。あとは遷移行列の2乗を計算すれば良い。分母の 10 は行列の外に出しておく。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\frac{1}{10}\left( \begin{array}{ccc} 1&4&4 \\ 7&2&3\\ 2&4&3 \end{array} \right)\right]^2 &=& \frac{1}{10^2}\left( \begin{array}{ccc} 37&28&28 \\ 27&44&43\\ 36&28&29 \end{array}\right) \\ \\ &=& \left( \begin{array}{ccc} 0.37&0.28&0.28 \\ 0.27&0.44&0.43\\ 0.36&0.28&0.29 \end{array}\right) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-aac31dd9db51d88183e03b103e2b693c_l3.png)
となる。したがって、今日の朝食が「ライス」である確率 ![]() は以下のように計算される。
は以下のように計算される。
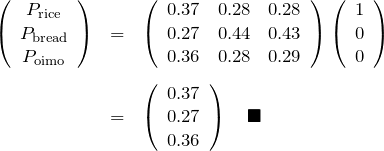
ついでに、今日の朝食が「パン」である確率 ![]() 、今日の朝食が「イモ」である確率
、今日の朝食が「イモ」である確率 ![]() も同時に求められた。
も同時に求められた。
2. n日後
今見てきたように、昨日の状態は一昨日の状態で決まる。さらに、一昨日の状態はその前日の状態によって確率的に決まっている。もっと過去からの遷移も考えることができるだろう。同時に未来についても確率的に予測できそうである。
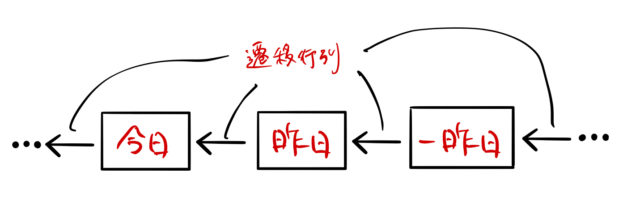
したがって、この確率遷移行列があれば未来の朝食も決定できそうである。今日から ![]() 日後にどうなっているか考えてみる。
日後にどうなっているか考えてみる。
今日の朝食が「ライス」であったときに、今日から ![]() 日後の朝食が「ライス」である確率を求めよ。
日後の朝食が「ライス」である確率を求めよ。
2.1 確率遷移行列をつくる
![]() 日後の状態が知りたいなら
日後の状態が知りたいなら ![]() 日後の状態を知れば良い。
日後の状態を知れば良い。![]() 日後の状態が知りたいなら
日後の状態が知りたいなら ![]() 日後の状態がわかればよい。先の例題の確率遷移行列で表現してみる。
日後の状態がわかればよい。先の例題の確率遷移行列で表現してみる。
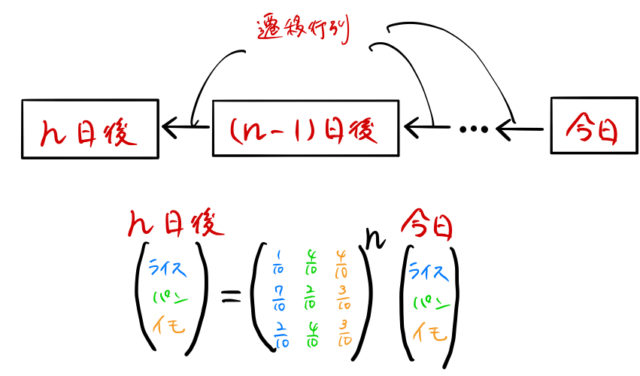
今日から ![]() 日後まで確率遷移行列は
日後まで確率遷移行列は ![]() 個ある。したがって遷移行列の
個ある。したがって遷移行列の ![]() 乗が知りたいのである。行列の
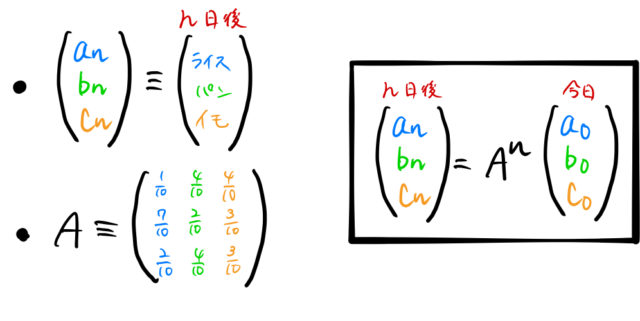
乗が知りたいのである。行列の ![]() 乗が知りたければ対角化をする。表記を簡単にするために、以下のようにベクトルと行列
乗が知りたければ対角化をする。表記を簡単にするために、以下のようにベクトルと行列 ![]() を取り決める。
を取り決める。
2.2 対角化と一般項
ここでは、行列の対角化は簡単に済ませる。固有値は以下の通りである。
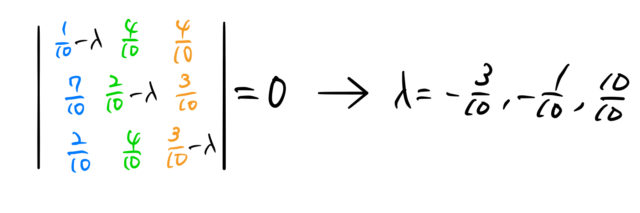
それぞれの固有値について固有ベクトルを求めて、![]() を対角化する行列
を対角化する行列 ![]() と
と ![]() を求めた。対角要素には、固有値
を求めた。対角要素には、固有値 ![]() が並ぶように
が並ぶように ![]() を作った。対角化行列は
を作った。対角化行列は ![]() とする。
とする。
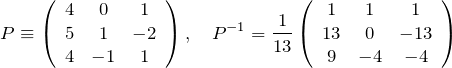
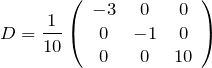
これより、![]() を求める。
を求める。
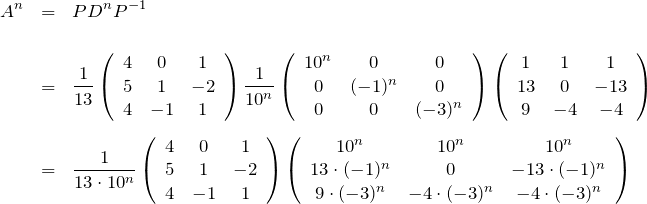
行列に入れると複雑なので要素ごとに書く( ![]() とする)。ただし、今日の状態は
とする)。ただし、今日の状態は ![]() ベクトルなので 1列目の成分だけ計算する。
ベクトルなので 1列目の成分だけ計算する。
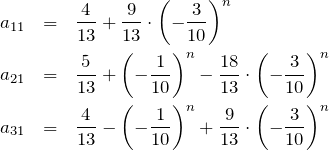
![]() :
: ![]() 日後の朝食が「ライス」である確率
日後の朝食が「ライス」である確率
![]() :
: ![]() 日後の朝食が「パン」である確率
日後の朝食が「パン」である確率![]() :
: ![]() 日後の朝食が「イモ」である確率
日後の朝食が「イモ」である確率
として計算する。
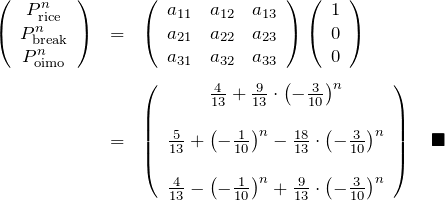
この答えは、![]() とすれば初めの例題の答えに一致する。
とすれば初めの例題の答えに一致する。
2.3 ∞日後の朝食
大学入試問題だと数列の一般項を求めて最後におまけのように極限の問題がついているので、ここでも同じように考えてみる。
![]() を考えれば
を考えれば ![]() 日後の朝食がわかります(地球があれば)。それぞれ、
日後の朝食がわかります(地球があれば)。それぞれ、![]() に収束します。
に収束します。
3. まとめ
ここでは単純なモデルを考えた。行列の対角化を用いれば ![]() 日後の状態まで考えることができることも学んだ。
日後の状態まで考えることができることも学んだ。
行列が複雑だと計算が大変になる。普通はこういう単純な計算はコンピュータに任せて、人間はいかに現象をモデル化するか考えるものである。