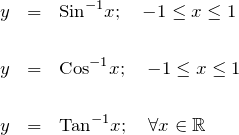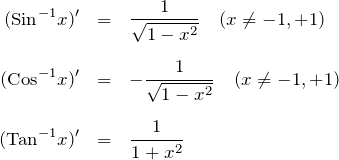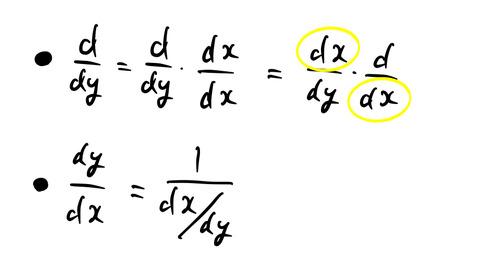逆三角関数を微分する。arcなんて付いてるが恐れるに足らない。はじめに微分する上で必要なことを学習する。その後、逆三角関数がいかにして定義されたかを学び、逆三角関数を微分する。ここで扱う方法は暗記が苦手な方でも微分できる方法だろう。
微分結果を先に載せておく。
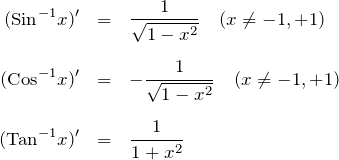
目次
1. 基礎知識
逆三角関数の微分を求める上で必要となる数学における基礎知識である。理解していると思う方は飛ばしてください。
1.1 三角比
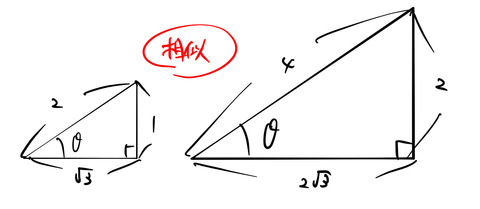
高校数学の復習をしよう。直角三角形で、図のように直角でない2つの角度のうち1つの角度を ![]() としよう。三角比とは「比」の話である。したがって左の1:2:
としよう。三角比とは「比」の話である。したがって左の1:2:![]() の三角形についての sin
の三角形についての sin![]() 、cos
、cos![]() 、tan
、tan![]() の値は、各辺を2倍にした相似な右の三角形のsin
の値は、各辺を2倍にした相似な右の三角形のsin![]() 、cos
、cos![]() 、tan
、tan![]() と同じである。当たり前である。
と同じである。当たり前である。
逆に言えば、sin![]() 、cos
、cos![]() 、tan
、tan![]() の値が与えられた時、その三角比を持つ三角形うち1つを描くことができる。例えば、
の値が与えられた時、その三角比を持つ三角形うち1つを描くことができる。例えば、![]() 、
、![]() を実数として sin
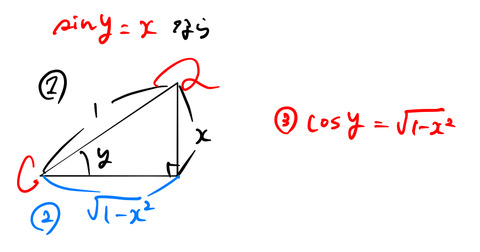
を実数として sin![]() =x が与えられているとする。そうすると、このような sin の値を持った直角三角形を、下のように見つけることができる。
=x が与えられているとする。そうすると、このような sin の値を持った直角三角形を、下のように見つけることができる。
斜辺は簡単のために1にしている。「比」さえあっていれば好きにすればいいが、ここではあえて複雑にとる必要もない。
いま、図のようなsinの値しか与えられていないが、具体的な三角形を描くと、cosとtanの値も容易に計算できる。今回使うのは cos![]() の値なので、cos
の値なので、cos![]() についてのみ説明する。結局、sin
についてのみ説明する。結局、sin![]() =
=![]() が与えられた時、cos
が与えられた時、cos![]() の値の求め方は以下の通りである。
の値の求め方は以下の通りである。
① sin![]() =
=![]() を満たす直角三角形を描く
を満たす直角三角形を描く
② 直角三角形から三平方の定理より残りの1辺の長さを求める
③ cos![]() の値を直角三角形からcos
の値を直角三角形からcos![]()
この方法では、よくある ![]() などの関係を使わないため、計算が簡単になっているように思う。
などの関係を使わないため、計算が簡単になっているように思う。
ここまでで見落としていることが1つある。それは、![]() (角度)が
(角度)が![]() [rad]=90 [度]を超える場合である。このときは図のような直角三角形に対して、cos
[rad]=90 [度]を超える場合である。このときは図のような直角三角形に対して、cos![]() となる。したがって、負号に注意する必要がある。
となる。したがって、負号に注意する必要がある。
以上のように具体的な直角三角形を描くことで、sinの値からcos(とtan)の値を容易に求められる。ただし、角度に注意した絵を描く必要があり、符号についても十分注意しなければならない。
1.2 微分のチェーンルール
微分の計算テクニック的な部分である(実際にはテクニックではなく意味のあるが今は考えない)。![]() は微分記号を表す。
は微分記号を表す。![]() は「
は「![]() で微分する」を表し、
で微分する」を表し、![]() は「
は「![]() を
を![]() で微分する」を表す。
で微分する」を表す。
黄色の部分が鎖のようにつながっていくためチェーンルールと呼ばれる。複数個繋げることもできる。
![]()
2個目の関係式は、あたかも「微分が分数であるかのように」逆数を使って変形している。この変形についても深入りはしない。以上の2式から分かる通り、微分を分数であるかのごとく扱うことがある。
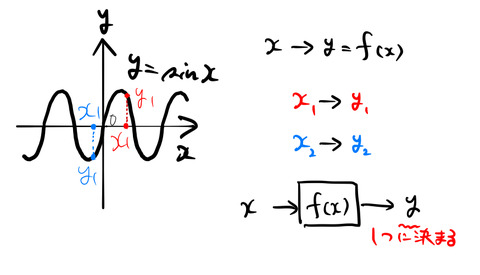
1.3 関数とは何だったか
図のように1つの入力(![]() )に対して、1つだけ出力
)に対して、1つだけ出力![]() がでる
がでる![]() を関数と呼ぶ。このとき、「
を関数と呼ぶ。このとき、「![]() は
は![]() の関数である」という。例えば、
の関数である」という。例えば、![]() に対して
に対して![]() が得られるし、
が得られるし、![]() に対して
に対して![]() が得られる。
が得られる。
図の![]() について、もちろん「
について、もちろん「![]() は
は![]() の関数である」。しかし逆に、
の関数である」。しかし逆に、![]() を決めても
を決めても![]() はひとつに決まらないことがある。例えば、
はひとつに決まらないことがある。例えば、
2. 逆三角関数の定義
逆三角関数は、
![]() 定義域:
定義域:![]()
![]() 定義域:
定義域:![]()
![]() 定義域:すべての実数
定義域:すべての実数 ![]()
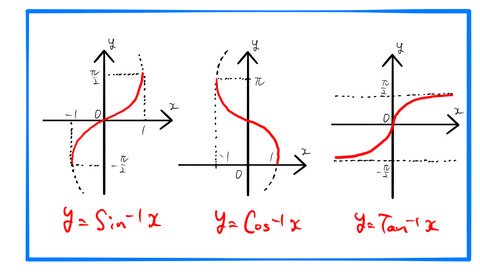
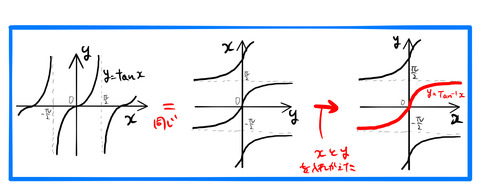
である。読み方はそれぞれ、アークサイン、アークコサイン、アークタンジェントである。絵は下の通り。
2.1 arcsin(x)
定義にさえ注意すれば、
![]()
![]()
![]() 定義域:
定義域:![]()
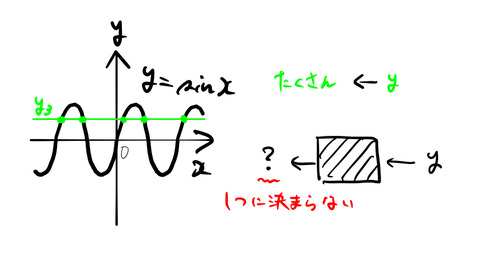
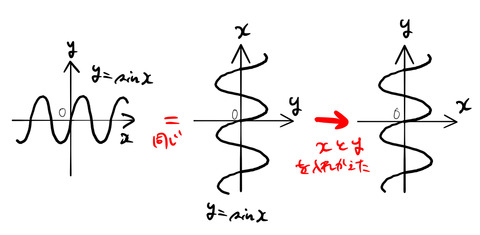
定義域を見るに、どうやら単純に ![]() は、単純に
は、単純に ![]() の
の ![]() と
と ![]() を入れ替えたものではない。実際に入れ替えてみると下のようになる。
を入れ替えたものではない。実際に入れ替えてみると下のようになる。
上図の一番右のように、![]() と
と ![]() を入れ替えは関数ではない。すなわち、
を入れ替えは関数ではない。すなわち、![]() の値に対して複数の
の値に対して複数の ![]() の値を取りうる(下図の左)。
の値を取りうる(下図の左)。
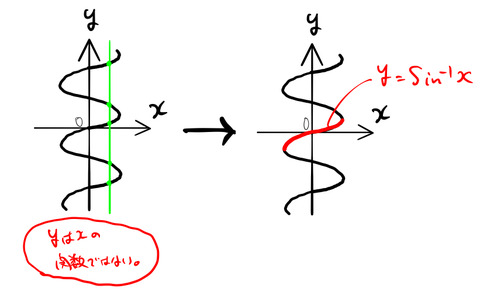
だから関数になりうるように(単調増加あるいは単調減少になるように)定義域 ![]() を設けた。この定義域では、上図の右における赤線(
を設けた。この定義域では、上図の右における赤線(![]() )は関数となっている。これがSin
)は関数となっている。これがSin![]() の正体である。
の正体である。
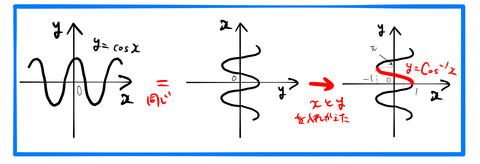
2.2 arccos(x)
![]() 定義域:
定義域:![]()
Sin![]() と同様に、関数になるようにCos
と同様に、関数になるようにCos![]() を作る。
を作る。
2.3 arctan(x)
![]() 定義域:すべての実数
定義域:すべての実数 ![]()
同様に、関数になるようにTan![]() を作る。
を作る。
3. 逆三角関数の微分
方針:![]() の形にして、両辺を微分する。
の形にして、両辺を微分する。
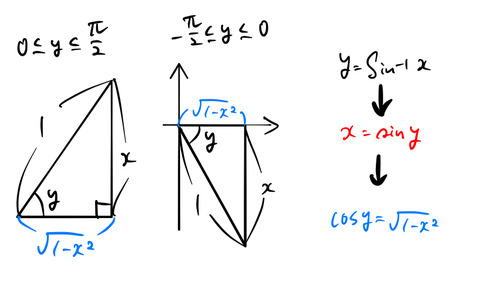
3.1 arcsin(x)
求めたいのは、![]() の微分
の微分 ![]() である。初めに、
である。初めに、
の両辺を ![]() で微分する。チェーンルールを使って、
で微分する。チェーンルールを使って、
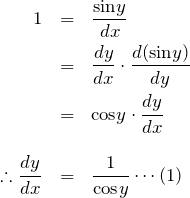
のようになる。cos![]() の値を求める。下図のように
の値を求める。下図のように ![]() =sin
=sin![]() を満たす直角三角形を書いて、cos
を満たす直角三角形を書いて、cos![]() を求めてみる。
を求めてみる。
![]() の値域は
の値域は ![]() である。このうち、符号に注意した2通りの
である。このうち、符号に注意した2通りの
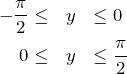
について、cos![]() の値は両方とも正である。(tan
の値は両方とも正である。(tan![]() の符号は異なることに注意。)三平方の定理より簡単に cos
の符号は異なることに注意。)三平方の定理より簡単に cos![]() の値がわかる。
の値がわかる。
![]()
これを式(1)に代入すると、
![]()
を得る。ただし分母が0となる![]() は除いた。
は除いた。
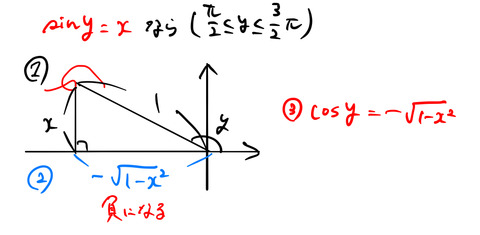
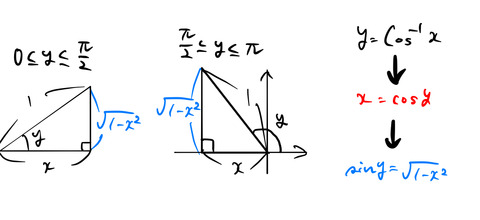
3.2 arccos(x)
同様に
![]()
の両辺を ![]() で微分する。チェーンルールを使って、
で微分する。チェーンルールを使って、
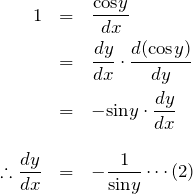
のようになる。sin![]() の値を求める。下図のように
の値を求める。下図のように ![]() =cos
=cos![]() を満たす直角三角形を書いて、sin
を満たす直角三角形を書いて、sin![]() を求めてみる。
を求めてみる。
![]() の値域は
の値域は ![]() である。このうち、符号に注意した2通りの
である。このうち、符号に注意した2通りの
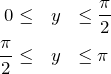
について、sin![]() の値は両方とも正である。(tan
の値は両方とも正である。(tan![]() の符号は異なることに注意。)三平方の定理より簡単に sin
の符号は異なることに注意。)三平方の定理より簡単に sin![]() の値がわかる。
の値がわかる。
![]()
これを式(2)に代入すると、
![]()
を得る。ただし分母が0となる![]() は除いた。
は除いた。
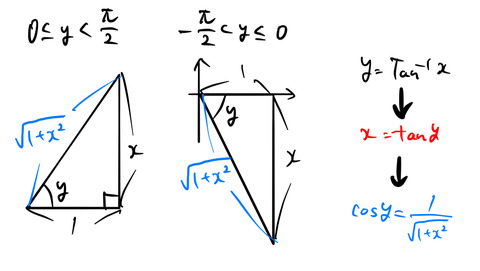
3.3 arctan(x)
同様に、
![]()
の両辺を ![]() で微分する。チェーンルールを使って、
で微分する。チェーンルールを使って、
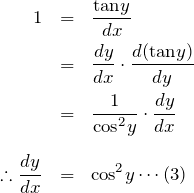
のようになる。cos![]() の値を求める。下図のように
の値を求める。下図のように ![]() =tan
=tan![]() を満たす直角三角形を書いて、cos
を満たす直角三角形を書いて、cos![]() を求めてみる。
を求めてみる。
いま、cosの値を2乗するので符号は関係ないが、一応調べておく。![]() の値域は
の値域は ![]() である。このうち、符号に注意した2通りの
である。このうち、符号に注意した2通りの
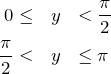
について、cos![]() の値は両方とも正である。(sin
の値は両方とも正である。(sin![]() の符号は異なることに注意。)三平方の定理より簡単に cos
の符号は異なることに注意。)三平方の定理より簡単に cos![]() の値がわかる。
の値がわかる。
![]()
これを式(3)に代入すると、
![]()
を得る。すべての実数![]() についてTanの微分は定義できる。
についてTanの微分は定義できる。
複素数の場合は、
![]()
になることに注意する。
4. 結果まとめ
最後にもういちど結果をまとめておこう。