ベイズの定理を学びましょう。はじめに迷惑メールの例をとって、条件付き確率を説明していきます。その後、事象がどのようになっているかを絵で学び、どのようにベイズの定理を導出するか考えていきます。最後まで読んで頂ければ、非常に簡単な内容になっていることがわかるでしょう。
![]()
式を見ても覚えられない人は、絵で公式を理解すれば忘れないでしょう。
1. ベイズの定理
統計学では、原因(因果)から結果を見る。しかし、ベイズの定理では、結果から原因を考えるのである。
例えば、迷惑メールを例にとろう。
![]() :「メールが迷惑メールである」確率
:「メールが迷惑メールである」確率![]() :「メールの文章に”お金”の文字を含む」確率
:「メールの文章に”お金”の文字を含む」確率![]() :「迷惑メールであり」「メールの文章に”お金”の文字を含む」確率
:「迷惑メールであり」「メールの文章に”お金”の文字を含む」確率
である。まず、原因![]() 結果については、
結果については、
「メールが迷惑メールである」![]() 「メールの文章に”お金”の文字を含む」確率
「メールの文章に”お金”の文字を含む」確率
であろう。しかし、実際に迷惑メールを見分ける時に必要なのは、
「メールの文章に”お金”の文字を含む」![]() 「メールが迷惑メールであった」確率
「メールが迷惑メールであった」確率
である。つまりこの場合、結果![]() 原因が重要なのである。
原因が重要なのである。
一般化して、事象 ![]() を原因 、事象
を原因 、事象 ![]() を結果とすれば、統計学とベイズの違いがわかる。
を結果とすれば、統計学とベイズの違いがわかる。
統計学:![]() (原因から結果を予測)
(原因から結果を予測)
ベイズ:![]() (結果から原因を予測)
(結果から原因を予測)
1.1 条件付き確率
条件付き確率は、ある事象が起こったときに別の事象が起こる確率を意味する。たとえば、統計学的な「メールが迷惑メールであるとき、そのメールの文章に”お金”の文字を含む」確率は条件付き確率である。
これは、![]() に対応する条件付き確率で、
に対応する条件付き確率で、![]() で表す。記号 “|” の右(
で表す。記号 “|” の右(![]() )が起こったという条件のもと、
)が起こったという条件のもと、![]() である確率を意味する。矢印の方向と
である確率を意味する。矢印の方向と![]() が逆なので注意してほしい。
が逆なので注意してほしい。
ベイズ的に見た、「メールの文章に”お金”の文字を含むとき、そのメールが迷惑メールであった」確率もまた条件付き確率である。
これは、![]() に対応する条件付き確率で、
に対応する条件付き確率で、![]() で表す。
で表す。
![]() :
:![]() が起こったという条件で
が起こったという条件で ![]() が起こる確率
が起こる確率![]() :
:![]() が起こったという条件で
が起こったという条件で ![]() が起こる確率
が起こる確率
(条件となる事象は”|”の右に置くことに注意する。)
1.2 絵で理解する
ベイズの定理を絵から導こう。事象 ![]() を原因、 事象
を原因、 事象 ![]() を結果とする。そうすると全事象
を結果とする。そうすると全事象
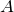 が起こるか起こらない
が起こるか起こらない が起こるか起こらない
が起こるか起こらない
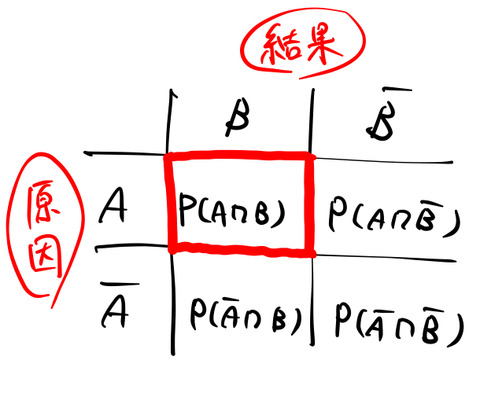
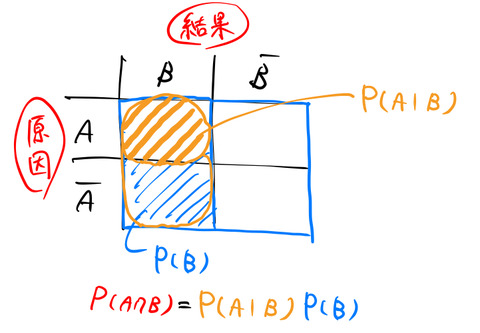
しかないので、下図のように4つに分類される。
赤枠で囲った部分が、![]() :「迷惑メールであり」「メールの文章に”お金”の文字を含む」確率である。この確率は、
:「迷惑メールであり」「メールの文章に”お金”の文字を含む」確率である。この確率は、
① ![]() が起こる
が起こる
② ![]() が起こった後(条件)で
が起こった後(条件)で ![]() が起こる
が起こる
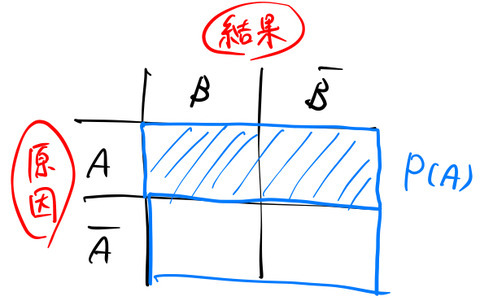
確率である。まず、「① ![]() が起こる」確率は、
が起こる」確率は、
の青の射線に対応する領域である。
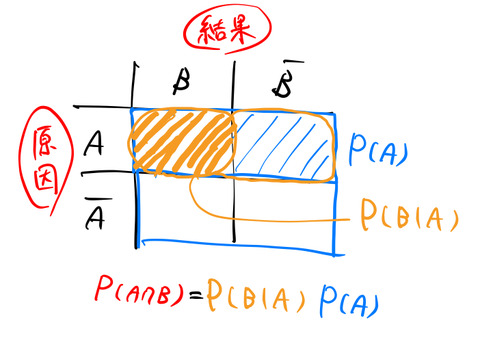
続いて、「② ![]() が起こった後(条件)で
が起こった後(条件)で ![]() が起こる」確率は、
が起こる」確率は、
のように、青の射線の中(条件)でオレンジの射線に対応する領域である。したがって、条件付き確率 ![]() により
により ![]() を表すことができる。つまり、
を表すことができる。つまり、![]() は①の確率
は①の確率 ![]() と②の確率
と②の確率 ![]() の積である。
の積である。
![]()
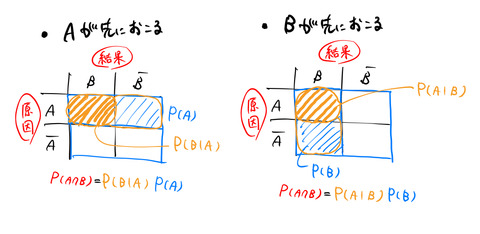
いま、![]() が先に起こる考えたが、
が先に起こる考えたが、![]() を先に起こると考えても良いはずである。したがって、
を先に起こると考えても良いはずである。したがって、![]() は、
は、
①’ ![]() が起こる
が起こる
②’ ![]() が起こった後(条件)で
が起こった後(条件)で ![]() が起こる
が起こる
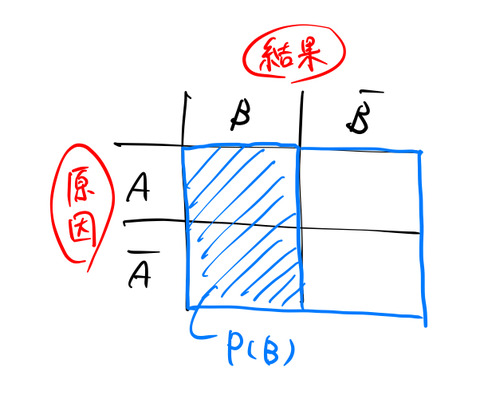
の確率としても表現できそうである。上と同様に、「①’ ![]() が起こる」確率は
が起こる」確率は
の青の射線に対応する領域である。
続いて、「②’ ![]() が起こった後(条件)で
が起こった後(条件)で ![]() が起こる」確率は、
が起こる」確率は、
のように、青の射線の中(条件)でオレンジの射線に対応する領域である。したがって、![]() を①’の確率
を①’の確率 ![]() と②’の確率
と②’の確率 ![]() の積でも表すことができる。
の積でも表すことができる。
![]()
上の2つパターンをまとめると、
となり、「確率を、縦から見るか?横から見るか?」*1の違いである。![]() は2つの表し方ができる。
は2つの表し方ができる。
![]()
1.3 結果から因果を見る
ベイズが知りたいのは、結果から原因(因果)であった。すなわち、 結果 ![]() が起こった時に原因が
が起こった時に原因が ![]() である条件付き確率
である条件付き確率 ![]() であった。上の式(*)の2つめの”=”の関係からベイズの定理が導ける。(両辺を
であった。上の式(*)の2つめの”=”の関係からベイズの定理が導ける。(両辺を ![]() で割る。)
で割る。)
![]()
絵を描いたら簡単に求められたと思いませんか。
![]() は、結果から原因を導く確率として「事後確率」とよばれる。何か事象が起こった後に、原因が何か突き止めるときに使われる。
は、結果から原因を導く確率として「事後確率」とよばれる。何か事象が起こった後に、原因が何か突き止めるときに使われる。
2. 例題1
例題を作ったので解いてみてほしい。
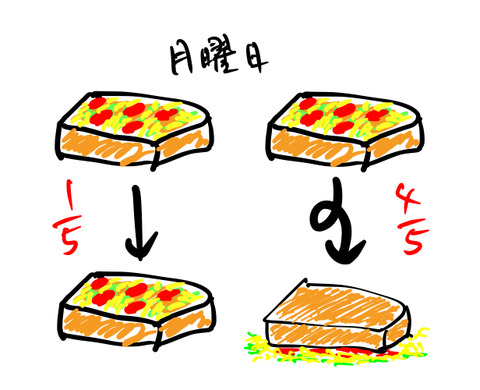
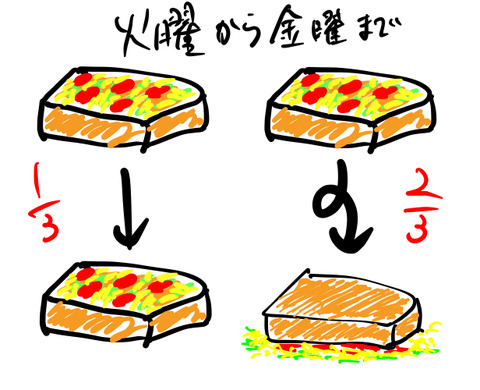
私は月曜から金曜日まで週に![]() 回、朝食にピザトーストを食べる。週に1回必ずトーストを落とすとする。月曜日にトーストを落としたとき、具材がのっている側が床に落ちる確率は
回、朝食にピザトーストを食べる。週に1回必ずトーストを落とすとする。月曜日にトーストを落としたとき、具材がのっている側が床に落ちる確率は ![]() である。火曜から金曜日にトーストを落としたときに、具材面が床につく確率は
である。火曜から金曜日にトーストを落としたときに、具材面が床につく確率は ![]() であるとする。具材面が床につく時、その日が月曜日である確率を求めよ。
であるとする。具材面が床につく時、その日が月曜日である確率を求めよ。
問題の様子は下のようになる。*2
【解答】
問題文より確率を下のように決める。
![]() :月曜日にトーストを落とす確率
:月曜日にトーストを落とす確率![]() :火曜日から金曜日にトーストを落とす確率
:火曜日から金曜日にトーストを落とす確率![]() :月曜日に落としたトーストの具材面が床につく確率
:月曜日に落としたトーストの具材面が床につく確率![]() :火曜日から金曜に落としたトーストの具材面が床につく
:火曜日から金曜に落としたトーストの具材面が床につく
求めたい確率は、
![]() :トーストの具材面が床についたとき、その日が月曜日である確率
:トーストの具材面が床についたとき、その日が月曜日である確率
である。以下のベイズの定理を利用する。
![]()
ベイズの定理を利用する問題では、![]() は直接与えられていないことがある。しかし、以下の関係により簡単に求めることができる。
は直接与えられていないことがある。しかし、以下の関係により簡単に求めることができる。
![]()
この場合、![]() の意味するところは、「トーストの具材面が床につく」確率である。いまの場合、
の意味するところは、「トーストの具材面が床につく」確率である。いまの場合、
① 月曜日にトーストを落として、具材面が床につく確率 ![]()
② 火曜日から金曜日にトーストを落として、具材面が床につく確率 ![]()
の和で与えられる。図の①②に対応する。
以上より、
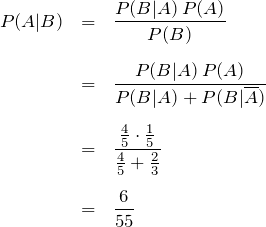
結局、「トーストの具材面が床についたとき、その日が月曜日である確率」は
ベイズの定理の分母を求めるときに、月曜日と月曜日以外に分けた。もし、それぞれの曜日で条件付き確率が違う場合は、
![]() :月曜日に落としたトーストの具材面が床につく確率
:月曜日に落としたトーストの具材面が床につく確率![]() :火曜日に落としたトーストの具材面が床につく確率
:火曜日に落としたトーストの具材面が床につく確率![]() :水曜日に落としたトーストの具材面が床につく確率
:水曜日に落としたトーストの具材面が床につく確率![]() :木曜日に落としたトーストの具材面が床につく確率
:木曜日に落としたトーストの具材面が床につく確率![]() :金曜日に落としたトーストの具材面が床につく確率
:金曜日に落としたトーストの具材面が床につく確率
ただし、![]()
として、
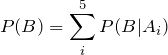
![]()
以上のようにベイズの定理の分母を条件付き確率の和で求めることにより、ベイズの定理は拡張できる。
![]()
3. まとめ
お絵かきすることで容易にベイズの定理が導けたと思います。定着させたいのであれば、自分で何も見ずに絵を描いてベイズの定理を導いてみるといいでしょう。少し復習すると定着度が格段に上がります。
お読みいただきありがとうございました。
*1「確率」を「打ち上げ花火」、「縦」を「下」に置き換えると映画作品にもなる。
*2 この問題の確率はマーフィの法則を恣意的に反映してみた。