X線は、ドイツ人物理学者、ヴィルヘルム・レントゲンによって発見され、レントゲンはその功績で1901年の第1回ノーベル物理学賞を受賞している。余談ではあるが、1903年には新しい放射線として「N線」なるものが報告されたが、後に誤りであったとされている。
X線の利用として、材料におけるX線回折が挙げられる。 X線の波長は 0.1〜100 Å であり、材料の格子定数や結晶中の原子間隔は数Åの世界と非常に近い。したがって、我々はX線回折により材料の結晶構造や格子定数を特定することができる。レントゲンの功績は、このように材料の世界へも大きな影響を与えている。
1. 連続X線の発生原理
X線には2種類ある。
- 連続X線: 連続的な波長(エネルギー)を持つ
- 特性X線: 特定の波長(エネルギー)を持つ
ここでは、「連続X線」の発生原理を説明しよう。
連続的な波長を持っているため、白色X線ともいう。 「白色」は、白色光がさまざまな色(波長)を持っていることに由来している。発生原理は、
- 電圧
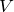 で電子を加速する
で電子を加速する - ターゲットに電子を衝突させる
- 衝突時の電子の運動エネルギーの損失に対応したX線が発生する
![]()
である。衝突後の電子の運動エネルギーは、
![]()
である。
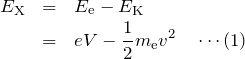
となる。X線の波長を ![]() とすれば、ド・ブロイの式より、
とすれば、ド・ブロイの式より、
![]()
式(2)を式(1)へ代入して整理すると、
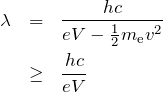
となる。不等号は、衝突後の電子の速度 ![]() がゼロ以上であることから成り立ち、等号成立は
がゼロ以上であることから成り立ち、等号成立は ![]() のときである。この下限の波長を
のときである。この下限の波長を ![]() として 短波長端という。具体的に、プランク定数
として 短波長端という。具体的に、プランク定数 ![]() [J
[J![]() s]、光速
s]、光速 ![]() [m/s]、電気素量
[m/s]、電気素量 ![]() [C] を代入して計算すると(単位に注意する)、
[C] を代入して計算すると(単位に注意する)、
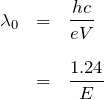
となる。ここで、加速した電子のエネルギー![]() の単位は[keV]である。単位を[keV]にしておくと便利である。例えば、100keVで電子を加速した場合は単に、
の単位は[keV]である。単位を[keV]にしておくと便利である。例えば、100keVで電子を加速した場合は単に、
![Rendered by QuickLaTeX.com \begin{eqnarray*}\lambda_0 &=& \frac{1.24}{100} \\ \\&=& 0.0124 \; {\rm [nm]}\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-acd6dead2000bd598ed7e080896f940f_l3.png)
となり、簡単に短波長端を計算することができる。
衝突した電子のエネルギー損失すべてがX線に変わるわけではない。ほとんどは衝突時に熱エネルギーに変わり、ターゲット金属は高熱になる。したがって、ターゲット金属を冷却しながらX線を発生させる。