ランジュバン関数とブリルアン関数の展開

ランジュバン関数 $L(x)$ （導出）とブリルアン関数 $B_J(x)$ （導出）の $x$ <<1における展開をする。これらの関数は、

$\begin{eqnarray*}L(x)&=&{\rm coth}(x)-\frac{1}{x}\\\\B_J(x)&=&\frac{2J+1}{2J}{\rm coth}\left(\frac{2J+1}{2J}x\right)-\frac{1}{2J}{\rm coth}\left(\frac{1}{2J}x\right)\end{eqnarray*}$

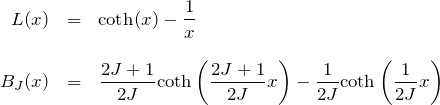
で与えられる。重要な coth( $x$ )の展開を用います。

coth(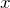 $x$ )の展開

$\begin{eqnarray*}{\rm coth}(x)=\frac{1}{x}+\frac{x}{3}+O(x^3)\end{eqnarray*}$

参考：coth(x)の展開（ランジュバン関数・ブリルアン関数の展開に必要）

1. ランジュバン関数の展開
2. ブリルアン関数の展開

1. ランジュバン関数の展開

coth(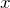 $x$ )の展開を用いれば簡単に、

$\begin{eqnarray*}L(x)&=&{\rm coth}(x)-\frac{1}{x}\\&=&\frac{1}{x}+\frac{x}{3}+O(x^3)-\frac{1}{x}\\ \\\therefore L(x)&=&\frac{x}{3}+O(x^3)\end{eqnarray*}$

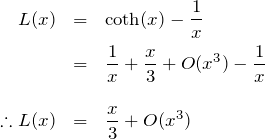
と展開できる。

ランジュバン関数 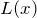$L(x)$ の展開

$\begin{eqnarray*}L(x)&=&\frac{x}{3}+O(x^3)\end{eqnarray*}$

2. ブリルアン関数の展開

少々計算が多いが、項ごとにそれぞれ展開する。

第１項：

$\begin{eqnarray*}&&\frac{2J+1}{2J}{\rm coth}\left(\frac{2J+1}{2J}x\right)\\ \\=&&\frac{2J+1}{2J}\Bigl[ \frac{2J}{2J+1}\,\frac{1}{x} + \frac{1}{3}\,\frac{2J+1}{2J}\,x+O(x^3)\Bigr]\\ \\=&&\frac{1}{x}+\frac{1}{3}\Bigl( \frac{2J+1}{2J} \Bigr)^2 \,x + O(x^3) \quad \cdots (1)\end{eqnarray*}$

第２項：

$\begin{eqnarray*}&&\frac{1}{2J}{\rm coth}\left(\frac{1}{2J}x\right)\\ \\=&&\frac{1}{2J}\Bigl[ \frac{2J}{x} + \frac{1}{3}\,\frac{x}{2J}+O(x^3)\Bigr]\\ \\=&&\frac{1}{x}+\frac{1}{3}\Bigl( \frac{1}{2J} \Bigr)^2 \,x + O(x^3) \quad \cdots (2)\end{eqnarray*}$

式(1) $-$ 式(2)より、

$\begin{eqnarray*}B_J(x)&=&\frac{1}{3}\Bigl( \frac{2J+1}{2J} \Bigr)^2 \,x -\frac{1}{3}\Bigl( \frac{1}{2J} \Bigr)^2 \,x + O(x^3) \\ \\&=&\frac{1}{3}\Bigl[ \left( \frac{2J+1}{2J} \right)^2 - \left( \frac{1}{2J} \right)^2 \Bigr] + O(x^3) \\ \\&=&\frac{1}{3}\, \left( \frac{1}{2J}\right)^2 \Bigl[ (2J+1)^2 - 1 \Bigr]+ O(x^3) \\ \\&=&\frac{1}{3}\, \frac{1}{4J^2} \, (4J^2 + 4J) + O(x^3) \\ \\&=&\frac{1}{3}\, \frac{1}{4J^2} \, 4J(J+1) + O(x^3) \\ \\&=&\frac{J+1}{3J}+O(x^3)\end{eqnarray*}$

となる。展開の結果として、ブリルアン関数 $B_J(x)$ の展開

ブリルアン関数の展開

$\begin{eqnarray*} B_J(x)=\frac{J+1}{3J}+O(x^3) \end{eqnarray*}$

を得る。

1. ランジュバン関数の展開

2. ブリルアン関数の展開

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル