ランジュバン理論は古典的な理論である。したがって量子力学的な話は登場しない。ここでは、ランジュバン関数の導出をおこなう。
- ランジュバン関数 ← あらゆる方向の磁気モーメント
- ブリルアン関数← 量子化された磁気モーメント
1. 基礎知識
ランジュバン関数導出のための基礎知識は以下の通り。
2. ランジュバン関数の導出
仮定:
- 相互作用のない原子の集団
- それぞれの原子は一定の磁気モーメント
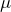 をもつ
をもつ 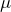 の方向はランダム → 古典統計
の方向はランダム → 古典統計
大きさ ![]() の磁気モーメントを持った原子の集団に、外磁場
の磁気モーメントを持った原子の集団に、外磁場 ![]() をかける。このとき、外磁場ベクトルと磁気モーメントのベクトルとの相互作用(エルギー)は、
をかける。このとき、外磁場ベクトルと磁気モーメントのベクトルとの相互作用(エルギー)は、
![]()
となる。磁場方向を向いている磁気モーメントのほうがエネルギーは小さい。
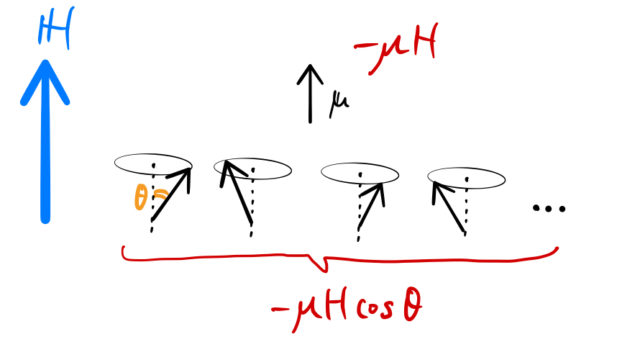
![]() は 外磁場と磁気モーメントの間の角度である。原子の磁気モーメントは全くランダムだと仮定しているため、集団全体で磁場に垂直な方向に値はでない。つまり、平均して相殺して 0 になる。
は 外磁場と磁気モーメントの間の角度である。原子の磁気モーメントは全くランダムだと仮定しているため、集団全体で磁場に垂直な方向に値はでない。つまり、平均して相殺して 0 になる。
したがって、磁場方向のみの値を考えれば良い。古典統計学ではエネルギー ![]() をもつ状態を取りうる確率は、以下のボルツマン因子に比例する。
をもつ状態を取りうる確率は、以下のボルツマン因子に比例する。
![]()
これは相対確率であり、確率の規格化のため分配関数で割る必要がある。つまり取りうる角度すべての確率を総和したもので割る。
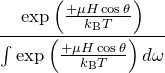
ここで、![]() は立体角である。原子数を
は立体角である。原子数を ![]() とすると、磁場方向の磁気モーメントの大きさ
とすると、磁場方向の磁気モーメントの大きさ ![]() は、
は、
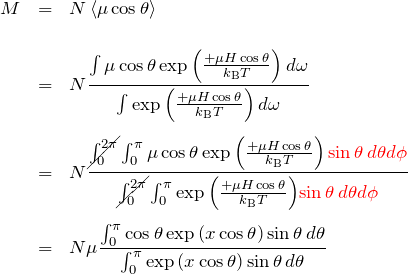
最後に ![]() とおいた。ここで、
とおいた。ここで、![]() と置いて積分を実行する。
と置いて積分を実行する。
分母:
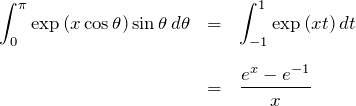
分子:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_0^{\pi} \cos\theta \exp{(x\cos\theta)}\sin\theta \, d\theta &=& \int_{-1}^{1} t\exp{(xt)}\,dt\\\\ &=& \left[\frac{1}{x}t\exp{(xt)}\right]_{-1}^{1} -\frac{1}{x}\textcolor{blue}{\int_{-1}^{1}\exp{(xt)}\,dt}\\\\ &=& \frac{e^x+e^{-x}}{x}-\frac{e^x-e^{-x}}{x^2} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e145d3e1d7db204ab1cf4d4147ab9997_l3.png)
部分積分を行なった。青色の部分は「分母」の積分を利用した。ちなみに分母の結果を ![]() で微分しても同様の結果を得る。
で微分しても同様の結果を得る。
以上より、
![Rendered by QuickLaTeX.com \begin{eqnarray*} M&=&N\mu \frac{\frac{e^x+e^{-x}}{x}-\frac{e^x-e^{-x}}{x^2}}{\frac{e^x-e^{-x}}{x}}\\\\\\ &=& N\mu \left[\coth x-\frac{1}{x}\right] \quad\left(\coth(x)=\frac{e^x+e^{-x}}{e^x-e^{-x}}\right)\\\\ &=& N\mu \textcolor{red}{L(x)} \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b2915e67e096a42d46eb1e9255aed5ad_l3.png)
である。
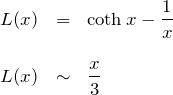
3. キュリー則
ランジュバン関数の展開を利用して、
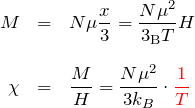
帯磁率 ![]() が温度
が温度 ![]() に反比例するキュリー則を得た。
に反比例するキュリー則を得た。
4. まとめ
ランジュバン理論は磁気モーメント間の相互作用を考えていないことに注意する。また、スピンの方向について量子化も考えていない。ランジュバン理論で考えなかった量子化を考慮するとブリルアン関数が導かれる。