磁性体のハミルトニアンを表すために、重要なハイゼンベルグ相互作用について説明する。ここでは軌道が重なっていない2つの原子軌道をイメージすればよい。また、軌道が重なった分子軌道に似た話は 電子ホッピングによる直接交換相互作用 の項で説明する。
ハイゼンベルグ相互作用は、以下のようにスピン演算子の内積の形で表される(ハイゼンベルグモデル)。
![]()
1. 3重項と1重項
2つの磁性原子を考え、それぞれの原子軌道に電子が1個ずつ入っている状態を考える。ハイトラーロンドンモデルと同様である。
2つの電子はスピン上向き(![]() )か下向き(
)か下向き(![]() )のどちらかの状態にある。つまり、下の4通りの状態にある。
)のどちらかの状態にある。つまり、下の4通りの状態にある。
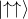 :電子1が上向き、電子2が上向き
:電子1が上向き、電子2が上向き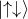 :電子1が上向き、電子2が下向き
:電子1が上向き、電子2が下向き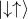 :電子1が下向き、電子2が上向き
:電子1が下向き、電子2が上向き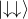 :電子1が下向き、電子2が下向き
:電子1が下向き、電子2が下向き
2つのスピンを合成した全スピン角運動量は ![]() である。規格直交化して、具体的に全スピンの状態を書いておく。
である。規格直交化して、具体的に全スピンの状態を書いておく。
3重項(triplet):![]()
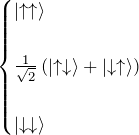
1重項(singlet):![]()
![]()
2つの電子スピンの入れ替えに対して、
- 3重項(
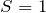 )は対称 → 軌道の波動関数
)は対称 → 軌道の波動関数 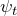 は反対称
は反対称 - 1重項(
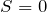 )は反対称 → 軌道の波動関数
)は反対称 → 軌道の波動関数 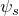 は対称
は対称
である。全体として波動関数が反対称となるように、2電子の軌道の波動関数は
![Rendered by QuickLaTeX.com \begin{eqnarray*} \psi_t(r_1,r_2)&=&\frac{1}{\sqrt{2}}\left[\Phi(\textcolor{blue}{r_{a1}})\Phi(\textcolor{blue}{r_{b2}})-\Phi(\textcolor{red}{r_{b1}})\Phi(\textcolor{red}{r_{a2}})\right] \\ \\ \psi_s(r_1,r_2)&=&\frac{1}{\sqrt{2}}\left[\Phi(\textcolor{blue}{r_{a1}})\Phi(\textcolor{blue}{r_{b2}})+\Phi(\textcolor{red}{r_{b1}})\Phi(\textcolor{red}{r_{a2}})\right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b08667aa5bf6732ee5080f0203603c4f_l3.png)
となる。注意として、上のようにスピンの波動関数(triplet,singlet)と軌道の波動関数(![]() )を独立に扱えるのは、スピン軌道相互作用を考えていないからである。
)を独立に扱えるのは、スピン軌道相互作用を考えていないからである。
2. ハイゼンベルグ相互作用
上の2つの軌道の波動関数 ![]() について電子間のクーロン斥力を考える。
について電子間のクーロン斥力を考える。
3重項についての電子間のクーロン斥力の期待値:
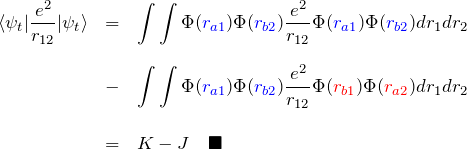
1重項についての電子間のクーロン斥力の期待値:
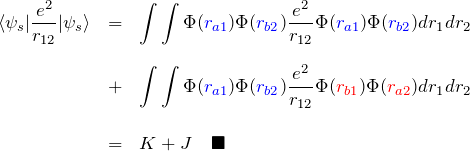
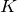 :直接積分
:直接積分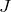 :交換積分
:交換積分
強磁性体の場合は ![]() であり、スピン3重項の状態のほうがエネルギーは小さくなる(
であり、スピン3重項の状態のほうがエネルギーは小さくなる(![]() )。
)。
ハイゼンベルグ相互作用を導出するために、スピン演算子 ![]() で3重項と1重項を表す。全スピン角運動量は
で3重項と1重項を表す。全スピン角運動量は ![]() である。したがって、
である。したがって、
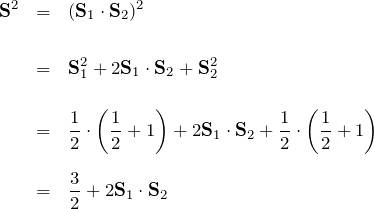
また、左辺は ![]() である。
である。
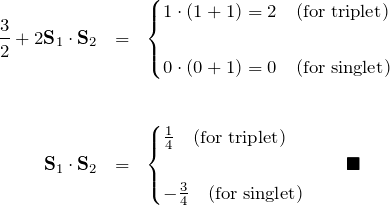
この ![]() を使って3重項と1重項を表すことができた。これを使うと電子間のクーロン斥力のエネルギーは
を使って3重項と1重項を表すことができた。これを使うと電子間のクーロン斥力のエネルギーは
![]()
このように各電子のスピン演算子の内積でスピン間相互作用を表示したものをハイゼンベルグモデルとよぶ。内積の形から以下のことがわかる。
 なら
なら 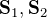 は平行が安定(強磁性的)
は平行が安定(強磁性的) なら
なら 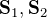 は反平行が安定(反強磁性的)
は反平行が安定(反強磁性的)
3. まとめ
3重項と1重項の軌道波動関数からハイゼンベルグ相互作用を導いた。このハイゼンベルグモデルは磁性体のハミルトニアンを表すためによく用いられる。このモデルではスピンが平行になるか反平行になるかは ![]() の符号を調べる必要がある。
の符号を調べる必要がある。