直接交換相互作用とは、隣接する原子の軌道にある2つの電子に働く相互作用である。ここでは、2つの原子間の電子のホッピングによる相互作用を考える。(運動交換ともいう。)
ハイゼンベルグ相互作用 の項では、2つの電子はそれぞれ2つの磁性原子の軌道に入っている状態を考えた。つまり、以下のような重なり積分が 0 の場合を考えていた。ここでは、軌道が重なった状態を考える。
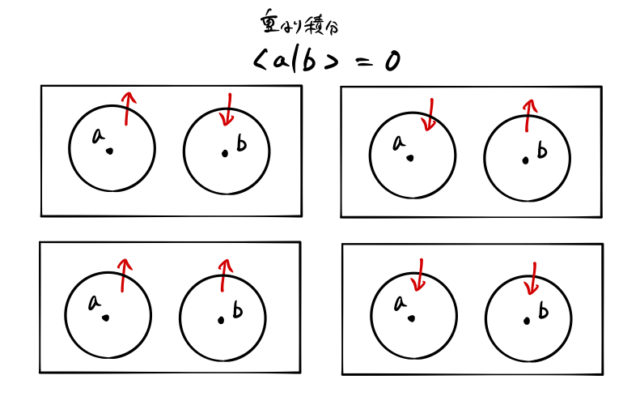
1. 重なり積分 <a|b> が0でない
重なり積分 ![]() であれば、各電子は各軌道に局在する。先述したハイゼンベルグモデルの項では、1重項(singlet)と3重項(triplet)のそれぞれの状態について軌道波動関数は以下のように与えた。
であれば、各電子は各軌道に局在する。先述したハイゼンベルグモデルの項では、1重項(singlet)と3重項(triplet)のそれぞれの状態について軌道波動関数は以下のように与えた。
![]()
それぞれの項は、原子 ![]() の原子軌道に電子1、原子
の原子軌道に電子1、原子 ![]() の原子軌道に電子2がある(また、その逆の)状態を表している。つまり、下の上図のような2つの原子軌道があるようなイメージに対応する。
の原子軌道に電子2がある(また、その逆の)状態を表している。つまり、下の上図のような2つの原子軌道があるようなイメージに対応する。
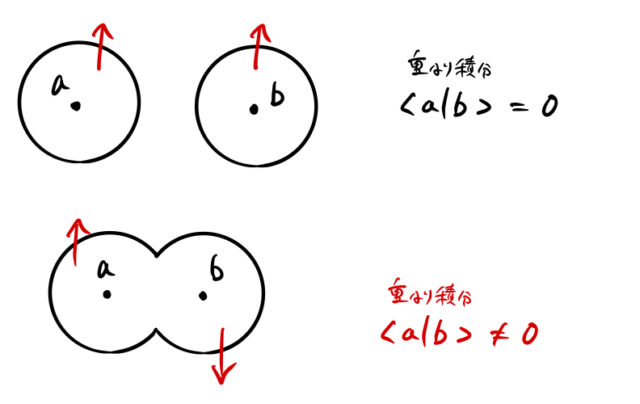
一方で重なり積分 ![]() のときは分子軌道のようなイメージになる。図では2つの電子はそれぞれ別の原子の周りにいると見なせる。しかし、2つの電子が
のときは分子軌道のようなイメージになる。図では2つの電子はそれぞれ別の原子の周りにいると見なせる。しかし、2つの電子が ![]() 側に寄っているかもしれないし、
側に寄っているかもしれないし、![]() 側によっているかもしれない。
側によっているかもしれない。
![]() のときは、
のときは、![]() 原子に元々いた電子が
原子に元々いた電子が ![]() 原子側にホッピングする可能性がある。
原子側にホッピングする可能性がある。
2. 電子のホッピングの特徴
電子のホッピングにより、どちらか1つの原子の軌道に2つの電子が詰まる。そして、もう一方の軌道には電子はなくなる。
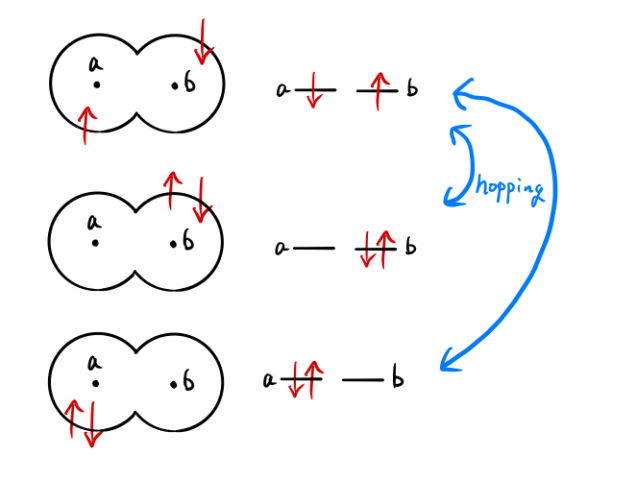
ただし、パウリの排他原理により同一軌道を同一スピンの2つの電子が占有することはない。つまり、上向きスピンの電子がホッピングする先の軌道は、下向きスピンが占有しているか、空でなくてはいけない。
クーロン斥力
電子のホッピングがおこると、同一軌道に2つの逆向きスピンをもった電子が存在する。2つの電子はともに負電荷を持っているためにクーロン斥力 ![]() が働く。電子ホッピングでエネルギー的にはクーロン斥力の分だけ損をする、ように見える。
が働く。電子ホッピングでエネルギー的にはクーロン斥力の分だけ損をする、ように見える。
摂動のエネルギー
電子ホッピングがおこった途中の状態だけ見るとクーロン斥力の分だけ損しているように見える。しかし、以下で見るように電子ホッピングの摂動のエネルギーを計算すると負になることが知られている。つまり、ホッピングによってエネルギーは下がる。
ホッピングの様子は以下の通りである。
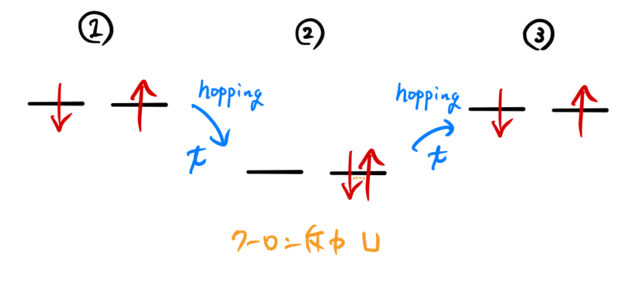
- ホッピングが起こる
- クーロン斥力によるエネルギー損
- 再度ホッピングが起こる(元に戻る)
このホッピングのエネルギーを摂動により求めてみる。まず、重なり積分 ![]() とする。
とする。![]() は電子のホッピングの運動エネルギーを意味する。
は電子のホッピングの運動エネルギーを意味する。
ここでは、![]() のように重なりが小さい場合を考える。つまり、2つの原子軌道を出発点としてホッピングを摂動として扱う。図のように2次の過程であり主要な項は、
のように重なりが小さい場合を考える。つまり、2つの原子軌道を出発点としてホッピングを摂動として扱う。図のように2次の過程であり主要な項は、
![]()
となる。また、ホッピング過程の摂動エネルギーは負であることがわかった。
反強磁性的相互作用
電子ホッピングが起こると同一軌道に逆向きスピンの2つの電子が詰められる。したがって、これは反強磁性的な相互作用である。例えば、水素分子の分子軌道がわかりやすい。結合性軌道には逆向きスピンが2つ詰められる。
3. まとめ
電子のホッピングによる直接交換相互作用を見てきた。これは重なり積分が 0 出ない場合に現れる。分子軌道のようなイメージである。ホッピングには以下のような特徴があった。
- 摂動のエネルギーは負になる
- 反強磁性的な相互作用
また、ホッピング以外の直接交換相互作用として、ハイゼンベルグ相互作用の項で考えたようなクーロン積分・交換積分があった。こちらは原子軌道を出発点として考えるイメージである。