例題
![]() で周期的な以下の関数
で周期的な以下の関数 ![]() をフーリエ級数に展開せよ。
をフーリエ級数に展開せよ。
![]()
1. 準備
グラフの概形
![]() のグラフは下のようになる。
のグラフは下のようになる。
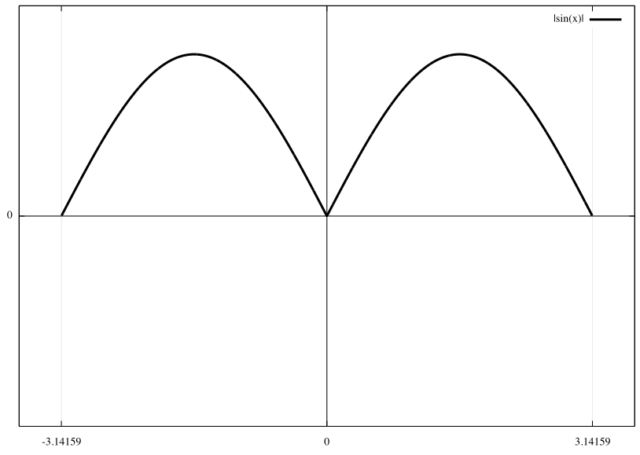
この関数は ![]() で偶関数である。
で偶関数である。
フーリエ級数展開/フーリエ係数
フーリエ級数で基本的に使うのは三角関数の直交性である。
三角関数の直交性
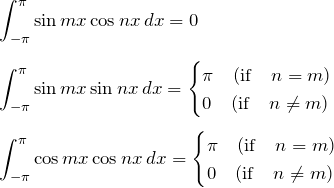
2.【解答】
周期関数 ![]() をフーリエ級数展開する。すなわち、周期
をフーリエ級数展開する。すなわち、周期 ![]() の三角関数で展開する。
の三角関数で展開する。
![]()
![]() が偶関数なので偶関数の
が偶関数なので偶関数の ![]() で展開できる。つまり、
で展開できる。つまり、![]() 。
。
ここで、両辺に ![]() をかけて、
をかけて、![]() で積分する(三角関数の直交性を利用する)。
で積分する(三角関数の直交性を利用する)。
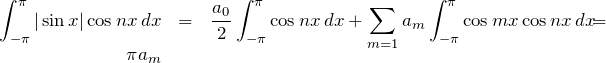
したがって、フーリエ係数は
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} a_m&=&\frac{1}{\pi}\int_{-\pi}^{\pi}|\sin x|\cos nx \, dx\\\\ &=&\frac{2}{\pi}\int_{0}^{\pi}\sin x \cos nx \,dx\\\\ &=&\frac{2}{\pi}\int_{0}^{\pi} \frac{1}{2}\left[ \sin (n+1)x -\sin(n-1)x \right]\, dx\\\\ &=& \frac{1}{\pi} \left[-\frac{\cos(n+1)x}{n+1}+\frac{\cos(n-1)x}{n-1}\right]_{0}^{\pi}\\\\ &=& \frac{1}{\pi}\left\{ \left(-\frac{\cos(n+1)\pi}{n+1}+\frac{\cos 0}{n+1}\right)+ \left(\frac{\cos(n-1)\pi}{n-1}-\frac{\cos 0}{n+1}\right) \right\}\\\\ &=& \frac{1}{\pi} \left\{-\frac{(-1)^{n+1}}{n+1}+\frac{1}{n+1} +\frac{(-1)^{n-1}}{n-1}-\frac{1}{n-1} \right\}\\\\ &=& \frac{1}{\pi} \left(1+(-1)^n\right) \left(\frac{1}{n+1}-\frac{1}{n-1}\right)\\\\ &=& \frac{-2}{\pi(n^2-1)}\left\{1+(-1)^n\right\}\\\\ &=& \begin{cases} 0\quad(n:\;{\rm odd},\;n\neq 1)\\\\ -\frac{4}{\pi(n^2-1)}\quad(n:\;{\rm even}) \end{cases}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8adfd0f30f69460f3a8aaf8be76dbd96_l3.png)
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} a_1&=&\frac{2}{\pi}\int_0^{\pi}\sin x\cos x \, dx\\\\ &=& \frac{1}{\pi}\int_0^{\pi} \sin 2x \, dx\\\\ &=& \frac{1}{2\pi}\left[-\cos 2x\right]_0^{\pi}\\\\ &=& \frac{1}{2\pi}\left(\cos 0-\cos 2\pi\right)\\\\ &=& 0\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b191e68b5b1bc535ae2b7a7564c51751_l3.png)
![]() のとき:
のとき:
![]()
まとめて、![]() のフーリエ係数は、
のフーリエ係数は、
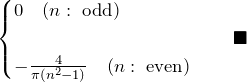
![]() のフーリエ級数展開は、
のフーリエ級数展開は、
![Rendered by QuickLaTeX.com \begin{eqnarray*} f(x)=|\sin x|&=&\frac{2}{\pi}+\sum_{n=2,4,6,...}^\infty \left[-\frac{4}{\pi(n^2-1)}\right]\cos nx\\\\ &=& \frac{2}{\pi}+ \sum_{m=1}\infty \left[-\frac{4}{\pi(4m^2-1)}\right]\cos 2mx\quad(n=2m)\\\\ &=& \frac{2}{\pi}-\frac{4}{3\pi}\cos 2x-\frac{4}{15\pi}\cos 4x -\cdots \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-6cc70fdb81c7a32bc907155545c2780e_l3.png)
おまけ:以下、4つの関数を比較した。
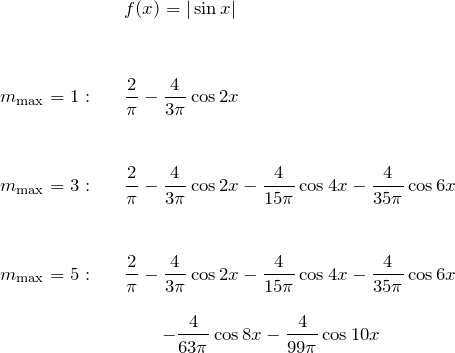
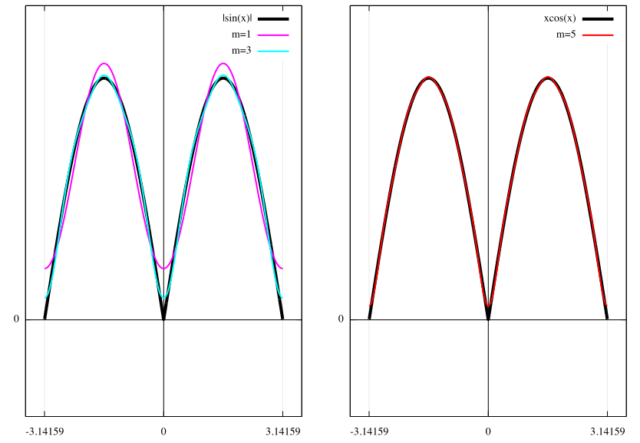
3. まとめ
この問題はよく出るのかもしれない。偶関数なので ![]() のみで展開できる。
のみで展開できる。