時間に依存しない摂動論(縮退なし)の概要とエネルギー計算を説明する。2次摂動までのエネルギーと波動関数は以下の通り。1次までで良い時は、2次摂動(赤色)は無視して計算すれば良い。(2次摂動の計算はそこそこ大変)
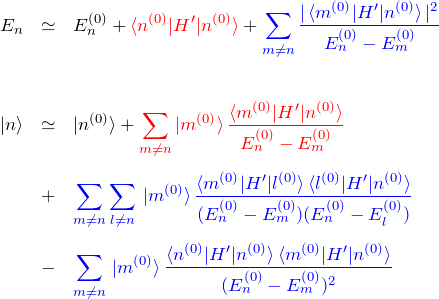
このとき、無摂動のハミルトニアン ![]() に対して、
に対して、![]() は既に解けているとする。
は既に解けているとする。
1. 摂動とは
既に方程式が解けている運動や状態に対して、比較的弱い相互作用が入ったときに、どのくらい変化するかを調べるのが摂動論である。
天王星の例がわかりやすいため、下の図で簡単に説明する。ケプラーの法則より天王星も太陽を焦点とする楕円軌道を描く(図左)。この運動は既知であるとする。
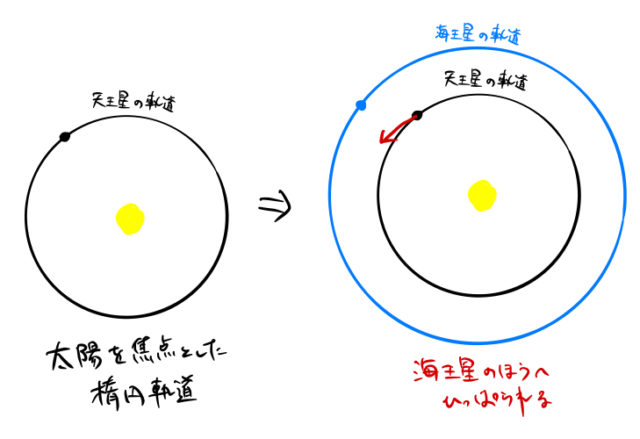
ここでの2次までの摂動は以下のように考えられる。太陽系の質量の99.9%を占める太陽の万有引力は大きく、以下の効果は比較的小さい。
1次摂動:天王星の外側の軌道にある海王星の万有引力によって天王星の運動が乱される(右図)。
2次摂動:天王星に引っ張られた海王星の軌道が変わる。新たな軌道上の海王星によって天王星が引っ張られる。
2次摂動は2ステップあることに注意する。つまり、まず別の新たな状態(海王星の新たな軌道)に遷移した後で、その新たな状態が元の状態(天王星の軌道)に影響を与えている。このことは、後にわかるように
![]()
に対応する。![]() のイメージである。
のイメージである。
2. エネルギー計算
2.0 ブラケットに慣れていないなら
ここでは以下のように読み替えてもらってもよい。
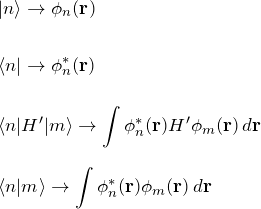
2.1 無摂動状態
与えられた無摂動ハミルトニアン ![]() に対して、無摂動のシュレディンガー方程式などが解けているとする。
に対して、無摂動のシュレディンガー方程式などが解けているとする。
![]()
ここで摂動論での 0 は無摂動を表す。![]() や
や ![]() は既知である。また、波動関数は規格化され直交しているとする。
は既知である。また、波動関数は規格化され直交しているとする。
![]()
複雑な問題の場合は、無摂動のシュレディンガー方程式などを解いてから、相互作用を摂動として取り込んでエネルギーや状態を求める。
概略図のように、摂動によりエネルギーが変化する。

2.2 摂動を入れる
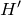 :
: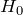 に対する摂動ハミルトニアン
に対する摂動ハミルトニアン-
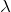 :摂動パラメータ(あとで1にする)
:摂動パラメータ(あとで1にする)
摂動が入ったハミルトニアン:
![]()
新たなハミルトニアン ![]() に対するシュレディンガー方程式:
に対するシュレディンガー方程式:
![]()
![]() に対して、
に対して、![]() はもはや固有状態ではないため、新たに摂動の影響を受けた状態
はもはや固有状態ではないため、新たに摂動の影響を受けた状態 ![]() を考える。その状態に対して新たなエネルギー固有値
を考える。その状態に対して新たなエネルギー固有値 ![]() が対応する。これらは、
が対応する。これらは、
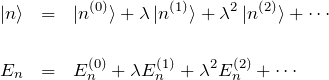
と展開しておく。展開を1次までで打ち切るなら
![]()
とすれば良い。ここでは、2次までの摂動を入れて計算する。
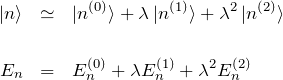
をシュレディンガー方程式に代入する。
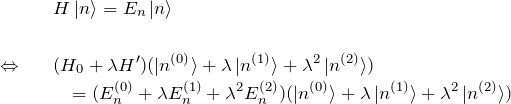
これを展開して ![]() のべきの係数を比較する。
のべきの係数を比較する。
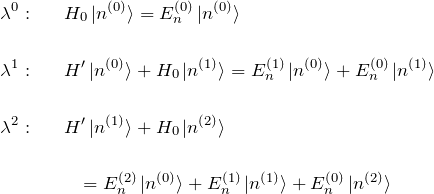
![]() は無摂動のハミルトニアンに対するシュレディンガー方程式で既知である。1次摂動については
は無摂動のハミルトニアンに対するシュレディンガー方程式で既知である。1次摂動については ![]() 、2次摂動については
、2次摂動については ![]() の方程式を解けば良い。
の方程式を解けば良い。
2.3 1次摂動まで
(1) ![]()
を解く。ここで以下を求めたい。
- 1次摂動のエネルギー
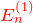
- 1次摂動の状態
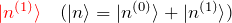
このとき摂動論を考える上で重要な展開がある。
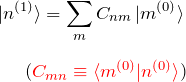
![]() を
を ![]() で展開してしまう。この展開により、
で展開してしまう。この展開により、![]() を求めるためには、展開係数
を求めるためには、展開係数 ![]() がわかれば良い。この展開を上の方程式へ代入すると、
がわかれば良い。この展開を上の方程式へ代入すると、
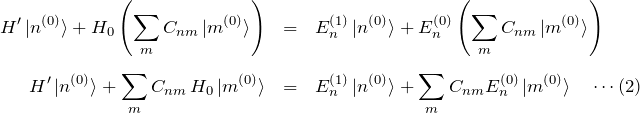
方針:無摂動の状態の直交性 ![]() を利用
を利用
式(2)の両辺に ![]() を作用させる:
を作用させる:
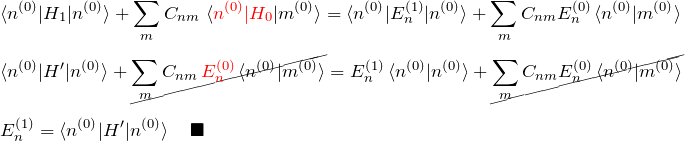
これが1次摂動によるエネルギーである。
式(1)の両辺に ![]() を作用させる:
を作用させる:
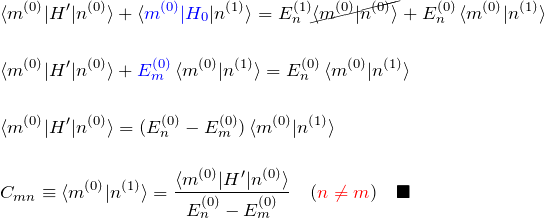
以上より、1次摂動まで取った時の ![]() と
と ![]() がわかる。
がわかる。
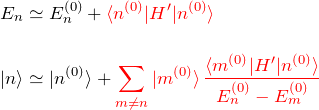
2.4 2次摂動まで
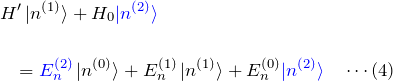
を計算する。以下を求めたい。
- 2次摂動によるエネルギー
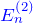
- 2次摂動による状態
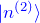
ここで、1次摂動までの結果から式(3)において以下は既知である。
- 無摂動ハミルトニアンの固有エネルギー
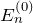
- 無摂動ハミルトニアンに対する固有状態
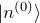
- 1次摂動によるエネルギー
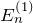
- 1次摂動による状態
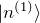
例によって ![]() を展開する。
を展開する。
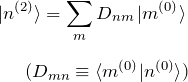
展開式を式(4) へ代入する。
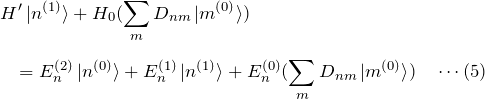
方針:
- 無摂動の状態の直交性
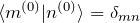 を利用
を利用 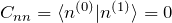 の利用
の利用
式(5)の両辺に ![]() を作用させる:
を作用させる:
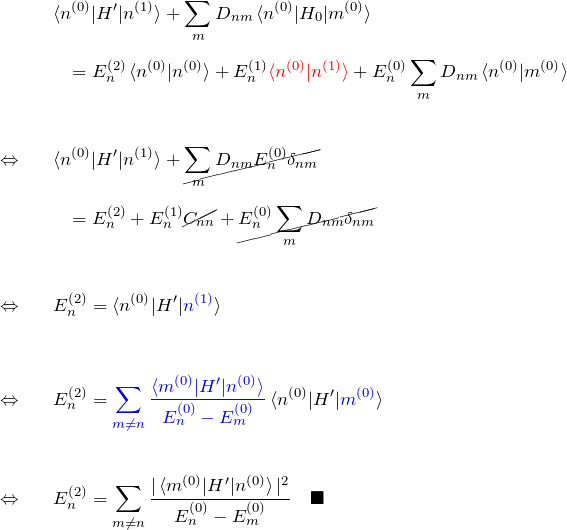
分母に ![]() がある。このことから、2次摂動では中間状態のエネルギー
がある。このことから、2次摂動では中間状態のエネルギー ![]() と、もとの状態のエネルギー
と、もとの状態のエネルギー ![]() との差が大きければ摂動の影響は小さいと言える。
との差が大きければ摂動の影響は小さいと言える。
式(4)の両辺に ![]() を作用させる:
を作用させる:
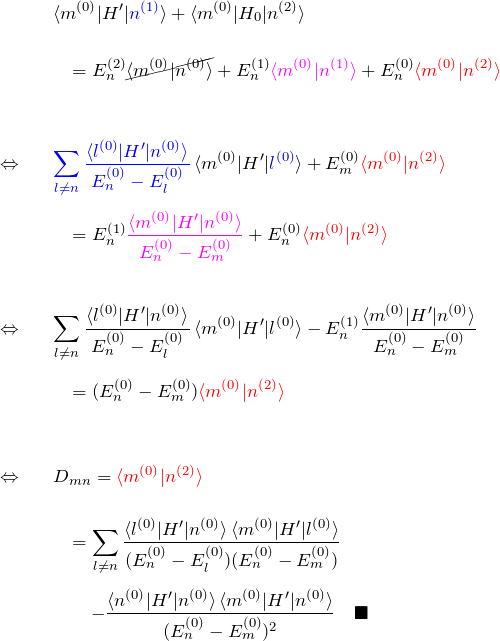
以上の結果を
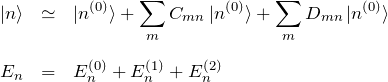
に代入することで、2次まで補正したエネルギーと状態がわかる。
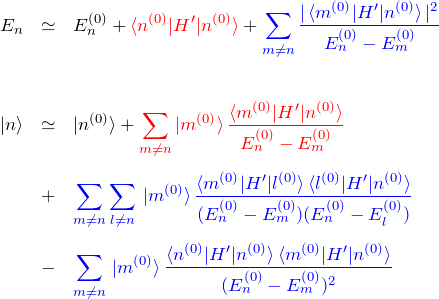
3. まとめ
摂動のエネルギー計算をしてきた。エネルギーの表式はよくでるので形を覚えておきたい。
![]() :この条件によって
:この条件によって ![]() となる。
となる。