インド生まれの数学者ラマヌジャンが見つけたクールな式を紹介する。目次の ![]() には複雑な式が入ります。一通り記事を読んでから、
には複雑な式が入ります。一通り記事を読んでから、![]() を穴埋め形式で使えるようにしています。ご活用ください(これは悪ふざけです)。
を穴埋め形式で使えるようにしています。ご活用ください(これは悪ふざけです)。
目次
1. ラマヌジャンって?
シュリニヴァーサ・ラマヌジャン(Srinivasa Ramanujan)は偉大な数学者である。1887年に生まれて、32歳という若さで亡くなったものの、その生涯に数えきれない功績を残している。
本記事では、連分数や円周率 ![]() の近似式の計算に長けた、「インドの魔術師」ラマヌジャンの見つけた式を紹介しよう。
の近似式の計算に長けた、「インドの魔術師」ラマヌジャンの見つけた式を紹介しよう。
2 分数・整数を忘れたら使う式
分数やら整数やら値がわからなくなった!というときに使えるかもしれない式です。私は覚えている派なので使ったことはないです。
2.1 □=1/2
もし、![]() が何かわからなくなったり、失われたときには以下の式を使うといいでしょう。
が何かわからなくなったり、失われたときには以下の式を使うといいでしょう。
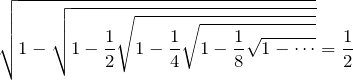
根号(ルート)が入れ子になっています。どこからこの式は来たのでしょう?
2.2 □=5/2
上のように、![]() を忘れる方はいませんね。もうちょっと複雑に行きましょう。 もし、
を忘れる方はいませんね。もうちょっと複雑に行きましょう。 もし、![]() が何かわからなくなったら以下の式を使うといいでしょう。
が何かわからなくなったら以下の式を使うといいでしょう。
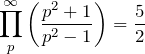
![]() は素数、
は素数、![]() は総乗を表します。つまり、
は総乗を表します。つまり、
![]()
と表すことができる。らしい。わかりやすいので、何項までが具体的に計算できそうです。
2.3 □=-2
中学生になると「負の数」を習います。理解できない学生がいたらそっと下の式を教えてあげましょう。
![Rendered by QuickLaTeX.com \begin{eqnarray*}\sqrt[3]{-6+\sqrt[3]{-6+\sqrt[3]{-6+\sqrt[3]{-6+\cdots}}}}=-2\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-05c9ba50b359f2f9ecad9d24d4627101_l3.png)
でもやっぱり立方根は難しいでしょうか?
2.4 □=3
そんなあなたに根号で表された式です。
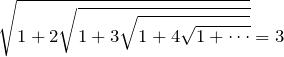
次からは超越数が入るので難しいです。
3. 連分数による公式、ネイピア数 e 関連
連分数による公式を紹介します。余談ですが、連分数はノートに手書きで書くと式のバランスがとりにくいです。![]() 関連の式が多いです。
関連の式が多いです。
3.1 □=1/(e-1)
右辺は分数だらけの連分数ですが、![]() を使って綺麗に表現できます。逆かもしれない。左辺が超越数だけど、右辺のように自然数で表すことができるほうが綺麗かもしれない。
を使って綺麗に表現できます。逆かもしれない。左辺が超越数だけど、右辺のように自然数で表すことができるほうが綺麗かもしれない。
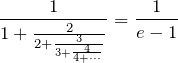
3.2 □=exp(π-1)/exp(π+1)
Euler’s identity ![]() みたいな形が現れる式。Eulerが好きそうな式でもある。
みたいな形が現れる式。Eulerが好きそうな式でもある。
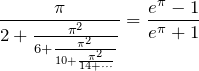
これは一般化もできる。
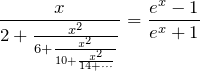
いろんな値を ![]() に代入して楽しむことができる式である。
に代入して楽しむことができる式である。
3.3 □=√(πe/2)
長い旅路の末、2つの超越数に結びつく衝撃的な結果となる。
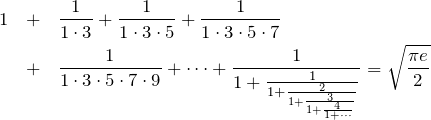
左辺の無限級数と連分数が、よく知られた ![]() と
と ![]() で表されるとは驚きである。
で表されるとは驚きである。
4. 円周率 π 関連
![]() は古代より近似値が求められてきた。 ラマヌジャンもその例にもれずいろいろな
は古代より近似値が求められてきた。 ラマヌジャンもその例にもれずいろいろな ![]() に関する式を発表している。
に関する式を発表している。
4.1 □≒π
近似精度は悪いだろうが、今まで以上に計算しやすい式である。
![]()
この式は8桁目まで正しい。
4.2 □=2/π
分母に ![]() があってもラマヌジャンには関係ない。
があってもラマヌジャンには関係ない。
![]()
次からはもっと激しい式を。
4.3 □=1/π (その1)
無限級数で表された ![]() の驚愕の表現。
の驚愕の表現。
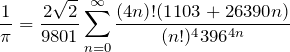
![]() に何か秘訣が?
に何か秘訣が?
4.4 □=1/π (その2)
最後に、二重階乗を使った見栄えがいい公式を紹介する。
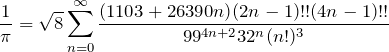
やっぱり、![]() に何か秘訣が?数式ですらエクスクラメーション。
に何か秘訣が?数式ですらエクスクラメーション。
5. おまけ:タクシー数
![]()
1729はタクシー数と呼ばれる。公式ではないが、ラマヌジャンの逸話として有名なので紹介しておく。ラマヌジャンの指導教官である、ハロルド・ハーディとの逸話は以下の通りである。
1918年2月ごろ、ラマヌジャンは療養所に入っており、見舞いに来たハーディは次のようなことを言った。
「乗ってきたタクシーのナンバーは1729だった。さして特徴のない数字だったよ」これを聞いたラマヌジャンは、すぐさま次のように言った。
「そんなことはありません。とても興味深い数字です。それは2通りの2つの立方数の和で表せる最小の数です」実は、1729は次のように表すことができる。
すなわち、1729が「A = B^3 + C^3 = D^3 + E^3」という形で表すことのできる数 A のうち最小のものであることを、ラマヌジャンは即座に指摘したのである。
このエピソードに見られるように、ラマヌジャンは直感的なひらめきに優れていますね。
6. まとめ
公式を通して、ラマヌジャンの常人離れしたすごさが見えたと思います。公式マスターを目指すためには、目次に戻って穴埋めを活用しましょう。今後、他にもおもしろい公式があったらまとめていきたいです。
お読みいただきありがとうございました。
7. 参考
ラマヌジャン以外にも面白い話が載っている本。

4.3の式のシグマが間違っています。kの無限級数ではなくて、nの無限級数です。
数学慣れしている人なら、「あ、ただの書き間違いかなー?」でスルーできる部分ではあるんですけどね。。。
少しでも多くの人にこんなスゲー数学者がいたことを知ってもらえることはとても大事なことだと思います。このようなページを設けてくださってありがとうございます!
(一般の理系大学生より)
ありがとうございます、大助かりです。
神秘的な人物なので興味深いと思いますし、式を眺めてるだけでもワクワクすると思います。
レジェンド数学者なので皆さまに知ってもらいたく、まとめた次第です。
2.2項の例示、合ってますか…?
この例えだと、答えは1になりませんか
すみません。このままだと左辺はちょうど1になります。
分母はマイナスでしたので、修正いたしました。
ご指摘ありがとうございます。