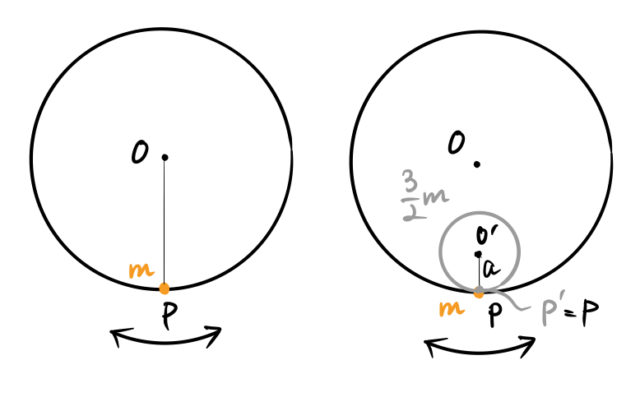
微小振動の例として円筒振り子がある。この円筒振り子の中にさらに円柱を入れて2つの微小振動を見る。以下の例題で考える。
左が厚みのない円筒の振り子。右が円筒振り子内の円柱(灰色)。
半径 ![]() の円筒振り子の軸まわりの慣性モーメント
の円筒振り子の軸まわりの慣性モーメント ![]() :
:
![]()
半径 ![]() 、質量
、質量 ![]() の円柱の軸周りの慣性モーメント
の円柱の軸周りの慣性モーメント ![]() :
:
この円柱の単位面積当たりの質量(面密度)は
![]()
である。慣性モーメントは半径 ![]() に依存する。したがって、下のような薄い半径
に依存する。したがって、下のような薄い半径 ![]() の円筒の慣性モーメントを
の円筒の慣性モーメントを ![]() で足し合わせれば
で足し合わせれば ![]() となる。この薄い円筒の質量は(面密度)×
となる。この薄い円筒の質量は(面密度)× ![]() である。
である。
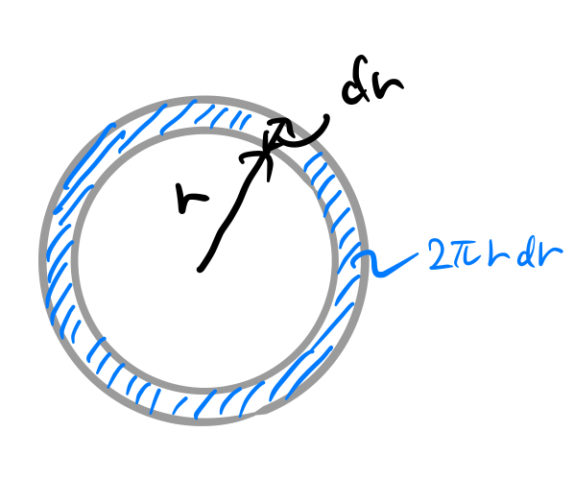
![Rendered by QuickLaTeX.com \begin{eqnarray*} I'&=&\int_{0}^{a}\left[\frac{3m}{2\pi a^2}\cdot 2\pi r dr \times r^2 \right]\\\\ &=& \frac{3m}{a^2}\int_{0}^{a} r^3 dr\\\\ &=& \frac{3}{4}ma^2 \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-0c272b7d52b81a38a1dc41e41ef11109_l3.png)
次に、円筒と円柱がそれぞれ基準位置からずれた場合を考える。下の図のように変数を設定する。
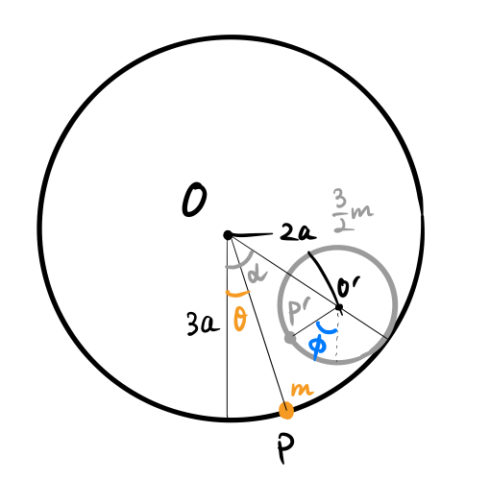
系の運動エネルギー ![]() は、
は、
- 円筒振り子の回転のエネルギー(
 について)
について) - 円柱の並進の運動のエネルギー(
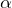 について)
について) - 円柱の回転の運動エネルギー(
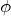 について)
について)
の和になる。ここで、運動エネルギーは慣性モーメント ![]() と角度
と角度 ![]() を用いて、
を用いて、
![]()
の形になることを利用する。また、円柱の重心の回転運動(![]() について)の 慣性モーメント
について)の 慣性モーメント ![]() は
は
![]()
である。以上より、系全体の運動エネルギー ![]() は
は
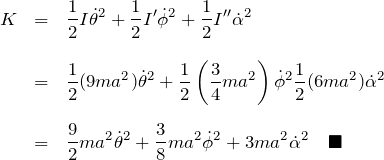
次に位置エネルギーを考える。系の位置エネルギーの総和 ![]() は
は
- 点
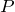 の位置エネルギー
の位置エネルギー 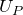
- 円柱重心の位置エネルギー
の和になる。微小振動の場合は ![]() であり、
であり、![]() を利用する。
を利用する。
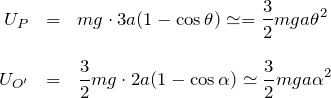
よって、系のポテンシャルエネルギー ![]() は、
は、
![]()
円柱が円筒をすべらない条件は、
![]()
で与えられるため、
![]()
より、運動エネルギー ![]() から
から ![]() を消去する。
を消去する。
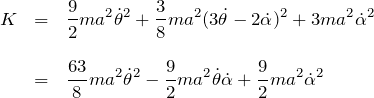
したがって、ラグランジアン ![]() は、
は、
![]()
となる。これより、オイラー・ラグランジュ方程式から![]() に関する連立運動方程式がわかる。
に関する連立運動方程式がわかる。
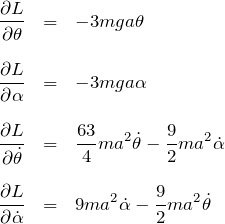
より、
![]() について:
について:
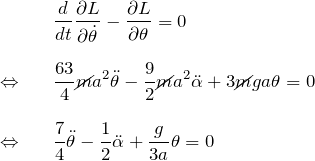
![]() について:
について:
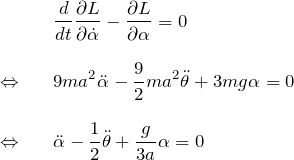
ここで、![]() とおいてまとめると、
とおいてまとめると、
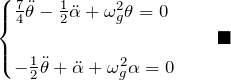
この連立微分方程式を解くために、
![]()
とおくと、
![]()
となる。これを微分方程式へ代入して、
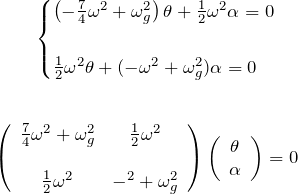
これが、自明な解(![]() )以外を持つためには行列式が
)以外を持つためには行列式が ![]() になる。
になる。
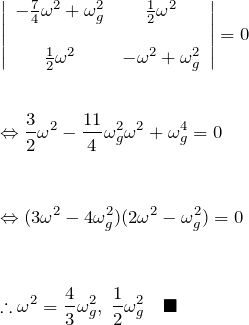
それぞれの固有値を ![]() とおく。この結果から、系の振動は
とおく。この結果から、系の振動は ![]() の基準振動の重ね合わせである(2質点の連成振動を思い出す)。
の基準振動の重ね合わせである(2質点の連成振動を思い出す)。
最後に固有関数(振動のモード)を求めると、
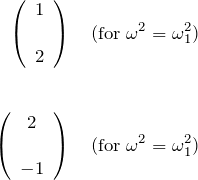
となる。したがって ![]() の振幅の比
の振幅の比 ![]() は固有関数の比、すなわち、
は固有関数の比、すなわち、
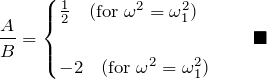
上で見てきたように、円筒振り子の中の円柱(微小振動)はそれぞれの基準振動を重ね合わせた振動となる。![]() の場合は、それぞれ微小振動で自由振動(単振動)として扱える。このような自由振動が重ね合わさるような運動は、2質点の連成振動となんら変わりない。
の場合は、それぞれ微小振動で自由振動(単振動)として扱える。このような自由振動が重ね合わさるような運動は、2質点の連成振動となんら変わりない。