立体角 ![]() の解説をおこないます。微小立体角と微小平面角の関係は以下。
の解説をおこないます。微小立体角と微小平面角の関係は以下。
微小立体角から微小平面角
![]()
1. 立体角の定義
平面角 ![]() のときを比べれば簡単にわかる。
のときを比べれば簡単にわかる。
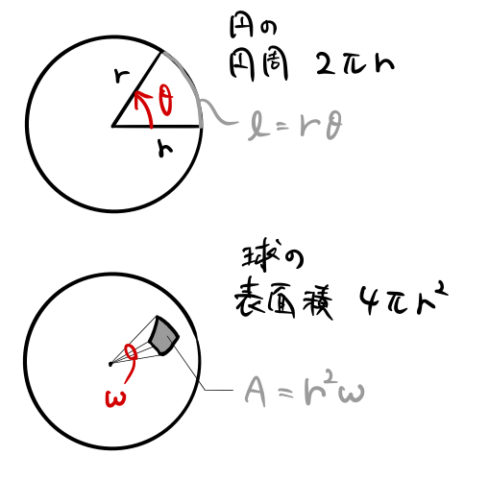
平面角、立体角の定義は、上図の半径 ![]() の単位円、単位球でおこなう。
の単位円、単位球でおこなう。
| 平面角 | 立体角 |
| 扇型 | 円錐 |
| 長さ | 面積 |
| 単位:ラジアン [rad] | 単位:ステラジアン [sr] |
以上、簡単にまとめた。
2. 立体角積分を平面角積分に
極座標表示で表した ![]() から角度
から角度 ![]() のみ微小変化させる。
のみ微小変化させる。
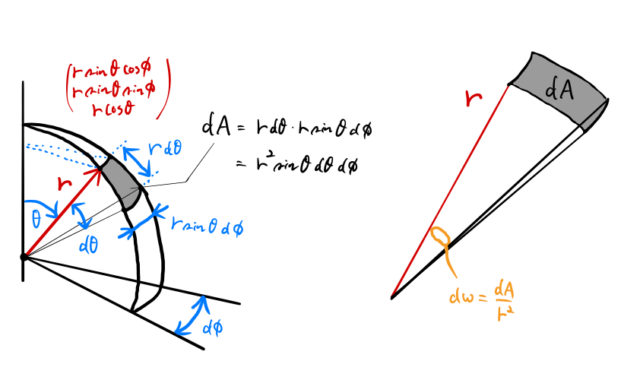
図より、微小変化 ![]() により面積は
により面積は
![]()
だけ増加する。![]() が一定の時、立体角の定義から
が一定の時、立体角の定義から
![]()
であるため、
微小立体角から微小平面角
![]()
3. まとめ
ちょくちょくでてくるのでメモとして残す。