複素積分の応用例として、以下の実積分を複素積分で解く。ちなみにこの実積分は講義積分で、 ![]() とすれば容易に解ける。
とすれば容易に解ける。
複素積分の例題
以下の実積分を複素積分を用いて解け(積分経路は少し下に与えた)。
![]()
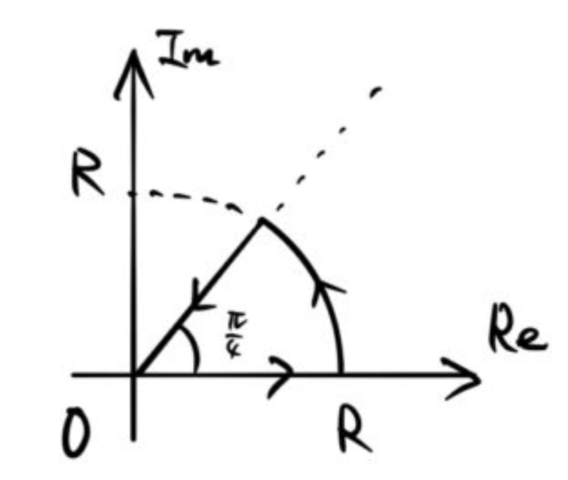
1. 複素積分の積分経路
積分経路は往々にして与えられる。今回の場合は以下の経路である。
赤線の経路 ![]() 上で
上で ![]() であり、例題の実積分に対応する。半円の半径は
であり、例題の実積分に対応する。半円の半径は ![]() として、図の矢印の向きに複素積分を実行する。
として、図の矢印の向きに複素積分を実行する。
2. 解答
複素関数を
![]()
とおく。複素平面全体で特異点は ![]() である(
である( ![]() は
は ![]() を除いて複素平面全体で正則である。)
を除いて複素平面全体で正則である。)
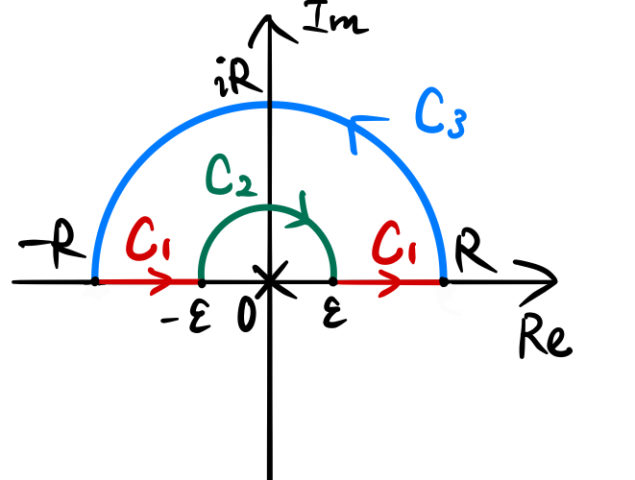
上の積分経路より、
![]()
になる。
C1上の積分
![]() は実軸の上にあるため、
は実軸の上にあるため、![]() である。したがって、
である。したがって、
![]()
最後に、![]() とすれば例題の積分に対応する。
とすれば例題の積分に対応する。
C2上の積分
![]() の点は
の点は
![]()
と置ける。また、
![]()
である。実際に積分を具体的に書いてみる。
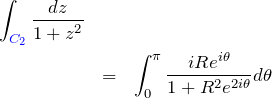
直接計算するのが難しいため、![]() のときの収束性を調べる。積分の絶対値をとって調べる(評価する)。このときのポイントは下の通り。
のときの収束性を調べる。積分の絶対値をとって調べる(評価する)。このときのポイントは下の通り。
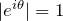 :
: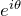 は複素平面上の単位円を表す
は複素平面上の単位円を表す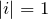 :複素平面上で大きさ1
:複素平面上で大きさ1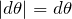 :積分の線素
:積分の線素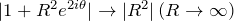 :
: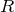 が1より十分大きいため
が1より十分大きいため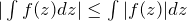
積分の絶対値(丁寧に):
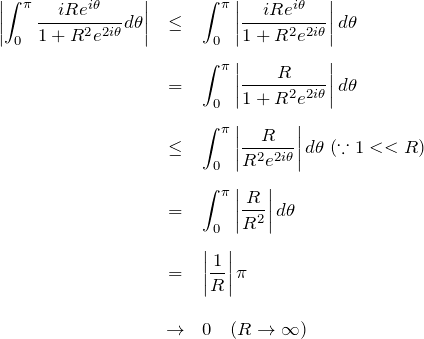
したがって、
![]()
結局、青色の積分経路 ![]() についての複素積分は
についての複素積分は ![]() で 0になる。
で 0になる。
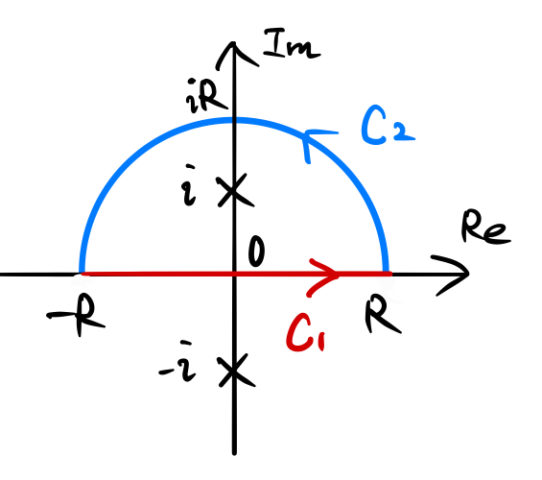
周回積分と留数定理
![]()
を計算する。積分経路 ![]() の中に特異点として
の中に特異点として ![]() を含む。したがって、特異点
を含む。したがって、特異点 ![]() の留数を
の留数を ![]() として留数定理より、
として留数定理より、
![]()
留数を求める:
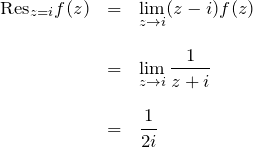
これより、
![]()
結果をまとめて実積分値を求める
上の3つの積分の結果をまとめる。![]() において、
において、
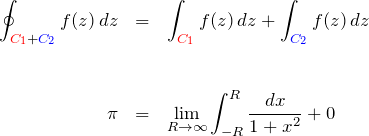
より、
![]()
3. まとめ
積分経路を工夫することで、実積分を複素積分を使って求めることができる。複素積分の問題傾向をまとめとる以下の通りである。
- 院試問題や定期試験のとき積分経路はだいたい与えられている
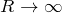 で円弧部分の積分はだいたい 0 に収束する
で円弧部分の積分はだいたい 0 に収束する- 特異点が経路内にあるか調べる。ある場合は留数定理を使う。
この問題は ![]() 使った方が早いが、複素積分の練習問題には良い。
使った方が早いが、複素積分の練習問題には良い。