最小二乗法の基本的な説明は以下に記載した。ここでは、2次元データ点に対して二次関数、三次関数のフィッティング式を導く。
二次関数でフィッティング
二次関数の場合は、与えられたデータ点に対して ![]() を求めれば良い。下図のように最も「うまい」フィッティングを探す方法の1つが最小二乗法であった。
を求めれば良い。下図のように最も「うまい」フィッティングを探す方法の1つが最小二乗法であった。
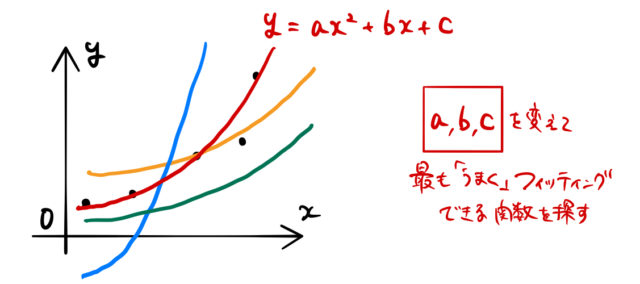
もっと数学的な概要を説明する。二次関数を ![]() とする。このとき、元のデータからの
とする。このとき、元のデータからの ![]() 方向のズレは
方向のズレは ![]() である。これを2乗してデータ数
である。これを2乗してデータ数 ![]() 個の総和をとったものを
個の総和をとったものを ![]() として、この
として、この ![]() を最小化するのが最小二乗法である。つまり、
を最小化するのが最小二乗法である。つまり、
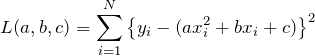
を最小にする ![]() の組を探す。
の組を探す。
Lを最小にする計算
与えられた ![]() が最小となる
が最小となる ![]() の条件は、
の条件は、
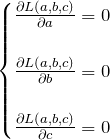
である。具体的に計算していく。以降、総和 ![]() は
は ![]() と略記する。
と略記する。
![]() で偏微分:
で偏微分:
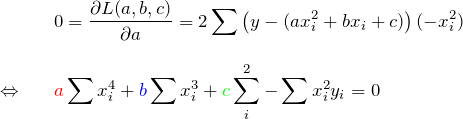
![]() で偏微分:
で偏微分:
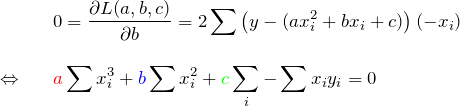
![]() で偏微分:
で偏微分:
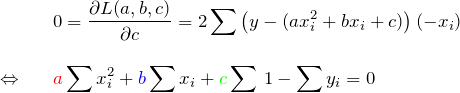
これらは ![]() に関する連立方程式である。行列で表示すると、
に関する連立方程式である。行列で表示すると、
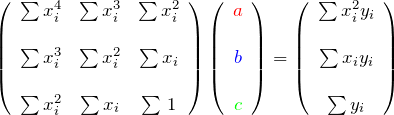
逆行列を作って、
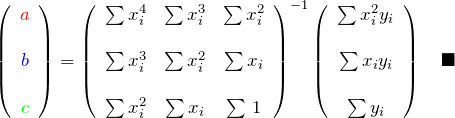
これで、![]() を求めて放物線
を求めて放物線 ![]() を作れば良い。
を作れば良い。
式自体は煩雑であるが、データ ![]() を累乗して足し合わせるだけなので単純な計算である。とは言っても手計算や電卓を使って計算するのも大変である。エクセルを使えば逆行列なども簡単に計算できるだろう。
を累乗して足し合わせるだけなので単純な計算である。とは言っても手計算や電卓を使って計算するのも大変である。エクセルを使えば逆行列なども簡単に計算できるだろう。
といっても、エクセルなどの表計算ソフトだったら二次関数のフィッティングぐらい機能として付いているはずである。
三次関数でフィッティング
![]() でフィッティングする。二次関数でのフィッティング式の結果から、
でフィッティングする。二次関数でのフィッティング式の結果から、
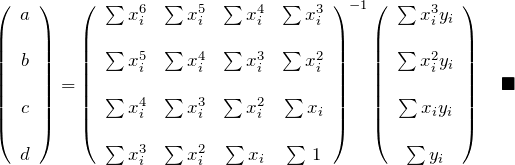
となる。![]() を作って偏微分するのも大変なので省略します。
を作って偏微分するのも大変なので省略します。
以上の結果から ![]() 次多項式でのフィッティングに対しては
次多項式でのフィッティングに対しては ![]() 次元の行列ができて、その逆行列を求めれば簡単にフィッティングできることがわかる。
次元の行列ができて、その逆行列を求めれば簡単にフィッティングできることがわかる。
まとめ
二次関数と三次関数について最小二乗法でのフィッティング方法をまとめた。まあ結局フィッティングはコンピュータがやってくれるけれど。