連成振動とは、バネで繋がった2個以上の質点が互いに相互作用しながら運動する振動のことである。質点が1個だけのときの振動より複雑になる。
質点2個の場合の連成振動の運動方程式を立てて解いていく。バネの復元力の向きがどっちに働いているっけ？ってなったときに使えるコツも書いていく。問題設定として以下の2通り用意した。ここでは水平ヴァージョンを扱う。
- 水平に2質点が並んでバネでつながっている場合 ←
- 垂直に2質点が並んでバネでつながっている場合
目次
1. 2質点の連成振動（水平）
以下のような水平に2質点がバネで繋がっている時の連成振動を考えよう。質量 
の質点について、つり合いの位置からの変位をそれぞれ 
として連成振動を見ていく。
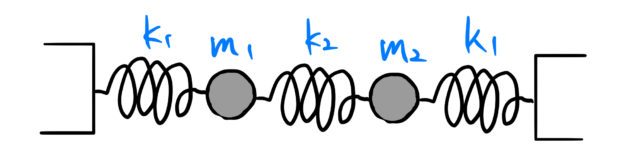
1.1 運動方程式を立てるコツ
運動方程式を立てるときはある状況の絵を描くと良い。運動方程式が立てやすい絵を描くコツは以下の通り。
- 右向きを正の変位とする
- より右にある
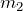の質点の変位 
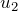は 
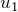より大きい
この状況を絵にしてみたのが下図である。
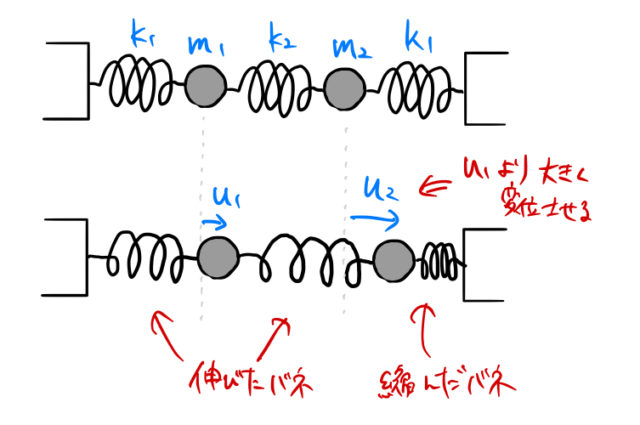
運動方程式を立てるためには、バネの復元力の向きが重要である。いまの絵では 
としているため、もともとのバネの長さから伸びたバネと縮んだバネは上の絵の通り簡単にわかる。バネの大きさは下図の通り。
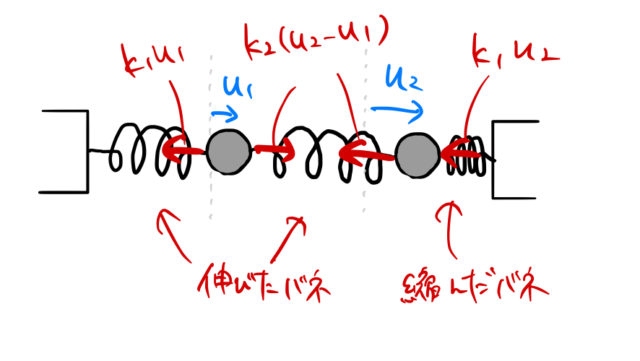
運動方程式を立ててみる。
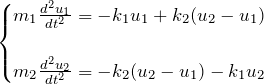
「 の特別な場合だけ考えていいの？」という疑問もあるが、
のときは逆符号になって運動方程式にあらわれるので問題ない。したがって、質点が2個の場合に限らず連成振動の問題では運動方程式の立てやすい絵を描くことが重要である。
1.2 運動方程式を整理、固有値問題
両辺をそれぞれ
で割って、整理しておく。
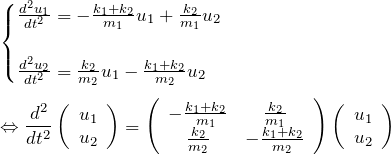
これは以下のように固有値問題であることがわかる。
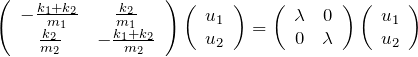
この固有値・固有関数は今考えている連成振動の2つの固有モードに対応する。
2. 固有値 λ を求める
「勤勉な読者のために固有値・固有関数を求めるのは各自でやってもらいたい。」と教科書にあるようなことを書きたかった。
以下では固有値方程式を解いている。上の行列を 
と置いた。
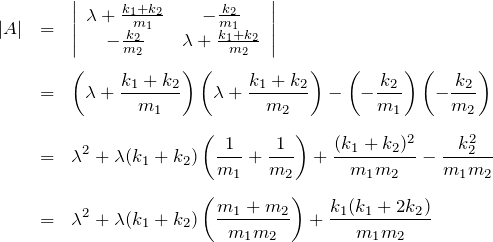
として、解の公式を使う。
ここで、
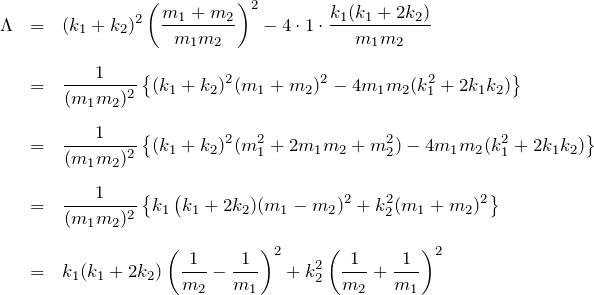
したがって、
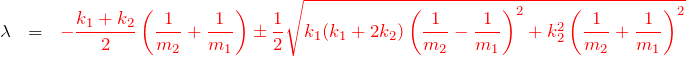
2.1 k1=k2=k （バネ定数が同じ時）
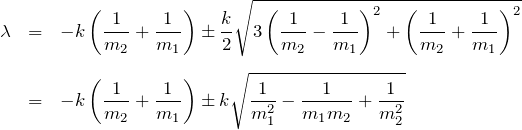
2.2 m1=m2=m （質量が同じ時）
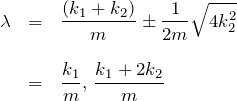
2.3 k1=k2=k かつ m1=m2=m
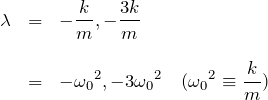
ここで新たに置いた 
は1個の質点だけがあるときの固有振動数である。
3. まとめ
固体物理では原子（格子点）の振動だと考えられる。実際には 
個の原子、周期境界条件などを課した連成振動を考える問題が多い。
個の質点に対しては、 個の振動モードが現れることだけ付け加えておく。