連成振動とは、バネで繋がった2個以上の質点が互いに相互作用しながら運動する振動のことである。質点が1個だけのときの振動より複雑になる。
質点2個の場合の連成振動(垂直型)の運動方程式を立てて解いていく。バネの復元力の向きがどっちに働いているっけ?ってなったときに使えるコツも書いていく。問題設定として以下の2通り用意した。ここでは垂直ヴァージョンを扱う。
- 水平に2質点が並んでバネでつながっている場合
- 垂直に2質点が並んでバネでつながっている場合 ←
目次
1. 運動方程式
以下のような垂直に2質点がバネで繋がっている時の連成振動を考えよう。質量 ![]() の質点について、つり合いの位置からの変位をそれぞれ
の質点について、つり合いの位置からの変位をそれぞれ ![]() として連成振動を見ていく。
として連成振動を見ていく。

初期状態を釣り合いの位置にすれば、重力は関係なくなる。水平のときと同じように解ける。
1.1 運動方程式を立てるコツ
運動方程式を立てるときはある状況の絵を描くと良い。運動方程式が立てやすい絵を描くコツは以下の通り。
- 下向きを正の変位とする
- より下にある
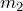 の質点の変位
の質点の変位 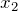 は
は 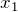 より大きい
より大きい
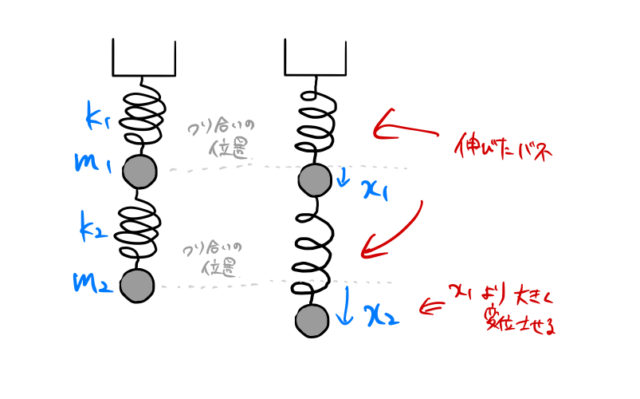
このように仮定して描いた絵が 上図の右 である。
バネの復元力の向きを調べるためにはバネが伸びているか縮んでいるか調べる必要がある。いまの絵では ![]() としているため、もともとのバネの長さから伸びたバネと縮んだバネは上の絵の通り簡単にわかる。バネの大きさは下図の通り。
としているため、もともとのバネの長さから伸びたバネと縮んだバネは上の絵の通り簡単にわかる。バネの大きさは下図の通り。
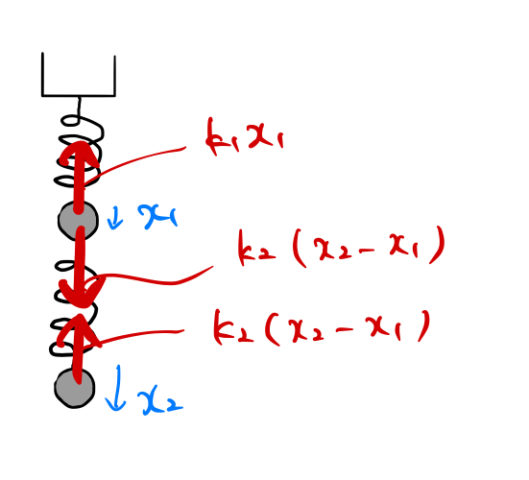
重力が描かれていないのは不思議に思えるかもしれないが、初期状態をバネの釣り合いの位置としているために重力は式にあらわれない。重力は初期状態におけるバネの自然長からの伸びによる復元力によって相殺されている。
初期状態の釣り合いの位置にあるバネの長さ ![]() バネの自然長
バネの自然長
であることに注意する。
1.2 運動方程式を立てる
図の状況にある時、容易に運動方程式を立てることができる。
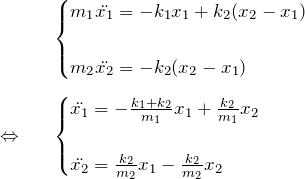
2. 行列を用いて運動方程式を解く(方針)
2.1 解の形を仮定する
基本解 ![]() と
と![]() 下のように定義する。
下のように定義する。
![]()
このとき、
![]()
であるから連立方程式は、
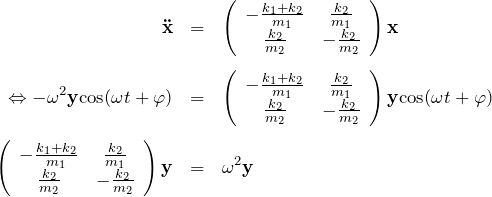
になる。ここで、行列 ![]() を、
を、
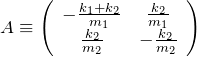
と表すことができる。
上記の固有値問題を解いて固有値と固有関数を求めることは重要である。この場合の ![]() は連成振動の固有振動数に対応する。
は連成振動の固有振動数に対応する。![]() は初期位相であり、
は初期位相であり、![]() の初期状態によって決定される。
の初期状態によって決定される。
3. 具体的な例題で学ぶ
例として、![]() のときを考える。この場合の連成振動の固有値・固有関数を求めて、固有振動を見てみよう。
のときを考える。この場合の連成振動の固有値・固有関数を求めて、固有振動を見てみよう。
以下は単なる行列の問題である。
3.1 固有値・固有関数を求める
![]()
である。固有値を ![]() と置くと、
と置くと、
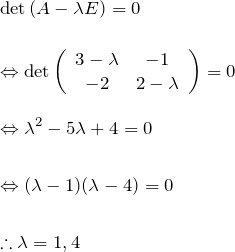
となる。以下で固有値の検算を忘れない。![]() と確かになっている。
と確かになっている。
![]() 次の正方行列Aとその
次の正方行列Aとその![]() 個の固有値に対して、
個の固有値に対して、
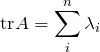
● 固有値を求める。
①![]() のとき、
のとき、
![]()
なので固有ベクトルの一つは、
![]()
となる。
②![]() のとき、
のとき、
![]()
なので固有ベクトルの一つは、
![]()
となる。2つの固有ベクトル(1)(2)より、
![]()
をつくる。
![]()
![]() の正方行列
の正方行列
![]()
![]()
![]() と
と![]() により
により![]() は対角化される。
は対角化される。
![]()
となる。固有ベクトルを並べた順に、対応する固有値が対角要素に並ぶ。
3.2 一般解を求める
もとの、
![]()
に戻って、この式の一般解を求める。対角化した行列を使える形にするために、両辺に左から![]() をかけて変形する。
をかけて変形する。
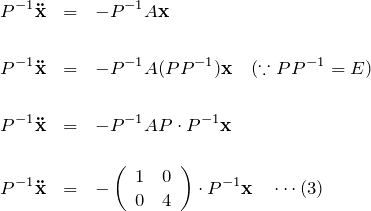
ここで、
![]()
を定義する。![]() を用いると式(3)は、
を用いると式(3)は、
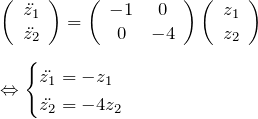
となり、それぞれ独立な2階の微分方程式となり容易に解ける。
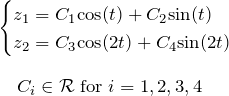
![]() を用いて、
を用いて、
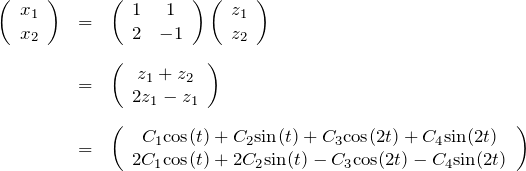
となり、一般解 ![]() が求められる。
が求められる。 ![]()
3.3 物理的な解法
なぜわざわざ(ii)では ![]() と置いたか。
と置いたか。
![]()
を見れば、行列 ![]() の固有値
の固有値 ![]() の関係にあることがわかる。今の場合
の関係にあることがわかる。今の場合 ![]() なので、
なので、![]() である。この角振動数
である。この角振動数 ![]() に対応する固有ベクトルがそれぞれの振動のモードとなる。すなわち、振動のモード(添字1,2で表す)は、
に対応する固有ベクトルがそれぞれの振動のモードとなる。すなわち、振動のモード(添字1,2で表す)は、
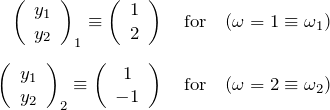
である。したがって、式(i)の一般解は、これらの振動(固有振動)を結合したものである。結合定数を ![]() 、初期位相を
、初期位相を![]() とすれば、
とすれば、
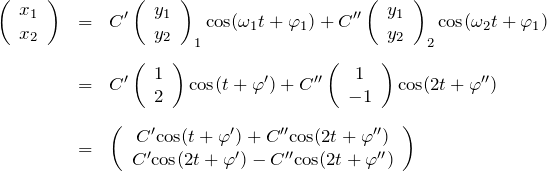
が一般解である。cosを展開すれば定数![]() が
が![]() で表すことができる。
で表すことができる。
4. まとめ
上で見てきたように、垂直に吊るされた質点の連成振動の場合も、初期状態を釣り合いの位置にとれば重力は考えなくて良い。結局、水平の場合と同様に解くことができることがわかる。
上の項目では、2質点が水平にバネで繋がった連成振動の問題の固有値をより一般的に求めているので参考にされたい。