固体物理で非常に重要なブリルアンゾーン(Brillouin zone)の項目である。3次元のブリルアンゾーンを考える前に、2次元で考えておくと理解しやすい。簡単な定義と体積の求め方を2次元について説明する。
1. ブリルアンゾーン
実空間におけるウィグナーザイツ胞に対応する。用語に惑わされてはいけない。単に隣の格子点との垂直二等分線で囲まれる領域のことである。3次元の場合は垂直二等分面である。
ブリルアンゾーンをざっくりと言う。
- 逆空間(
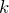 空間)にある
空間)にある - 逆格子点の垂直二等分面で囲まれる領域
第一ブリルアンゾーンは最近接の格子点との垂直二等分面で囲まれる領域、第二は最二近接の格子点との垂直二等分面で囲まれる領域で第一ブリルアンゾーンの外にある。
1.1 正方形の逆格子点のブリルアンゾーン
はじめに最も単純な場合を考える。以下のような逆格子点をもった空間でブリルアンゾーンを考えてみる。格子点間隔は実空間の格子定数 ![]() によって、
によって、![]() で与えられる(逆格子ベクトルの定義から)。
で与えられる(逆格子ベクトルの定義から)。
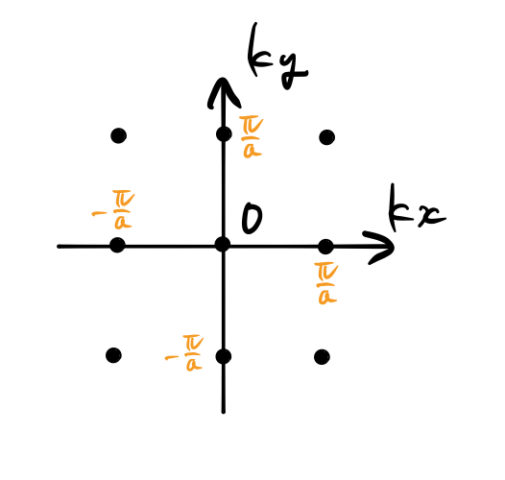
第一ブリルアンゾーンと第二ブリルアンゾーンを求めてみる。下のように作図すればよい。
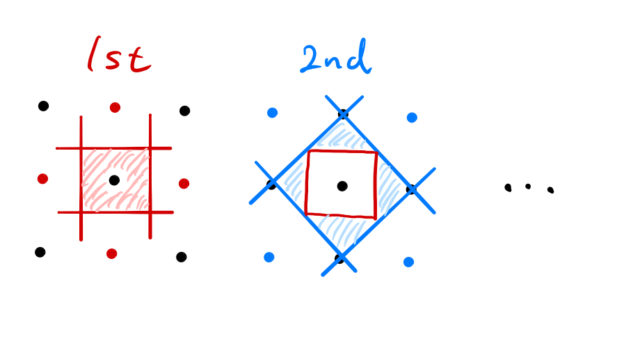
赤点が第一近接、青点が第二近接の逆格子点である。垂直二等分線を引いて求めれば良い。
第一ブリルアンゾーンの面積 ![]() は容易に、
は容易に、
![]()
だとわかる(赤射線の正方形の面積に対応)。
1.2 六角形の逆格子点におけるブリルアンゾーン
逆格子ベクトルが直角でない場合は、図のように「六角形」のように逆格子点が配置される。
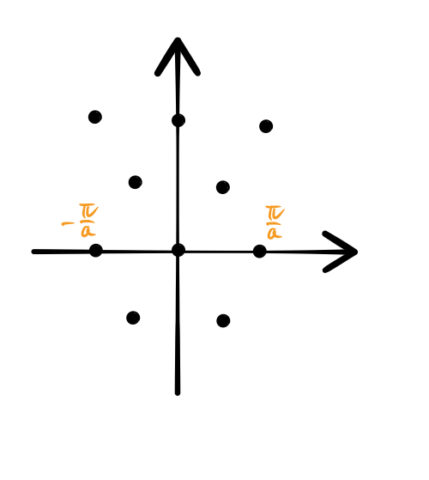
第一ブリルアンゾーンを求める。下図の通りである。
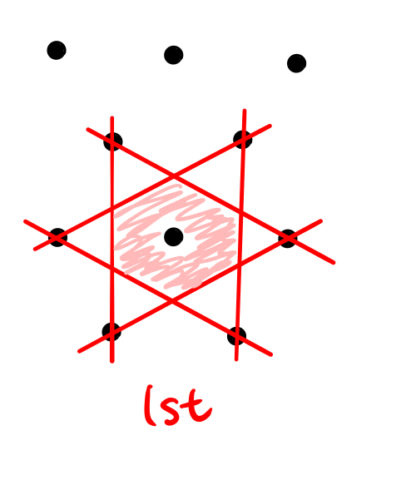
ここで、赤射線で表された第一ブリルアンゾーンの面積 ![]() を求める。
を求める。
このとき1stブリルアンゾーンの意味を考える。ウィグナーザイツセルの取り方から以下の重要なことがわかる。
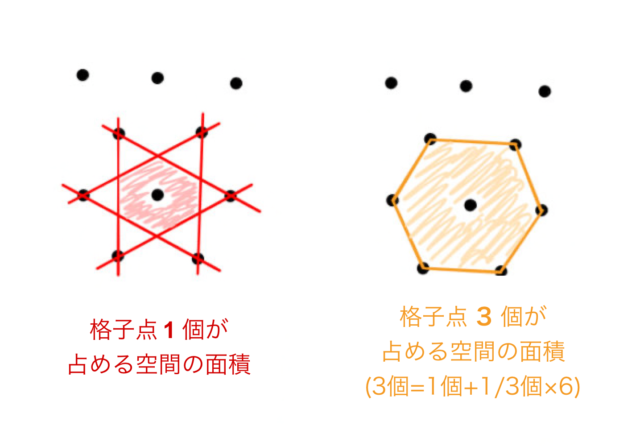
1stブリルアンゾーンを単位として全空間を埋めることができる。つまり、1stブリルアンゾーンの面積は空間において1個の逆格子点が占める領域の面積と同じである
上の図にあるような赤い六角形はとなりの格子点でも同じ形をしている。したがって、全空間を1stブリルアンゾーンで埋めることができるのである。
第一ブリルアンゾーンの面積 ![]() を求めるためには、オレンジの面積
を求めるためには、オレンジの面積 ![]() を求めて3で割れば良い。
を求めて3で割れば良い。
逆格子点間隔を ![]() とすると、オレンジの領域(正六角形)の面積は、
とすると、オレンジの領域(正六角形)の面積は、
![]()
である。したがって、求める面積は
![]()
である。
2. 3次元のブリルアンゾーンの体積
上の話は3次元にも拡張できる。
3つの逆格子ベクトル ![]() で定義される逆格子空間について、1stブリルアンゾーンの体積
で定義される逆格子空間について、1stブリルアンゾーンの体積 ![]() を求める。
を求める。
つまり、逆格子点1個が占める逆格子空間における体積を求めれば良い。
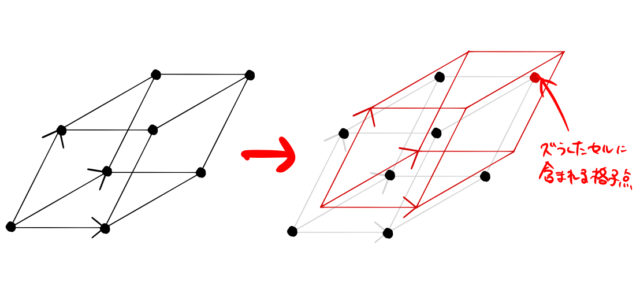
一般に3つの逆格子ベクトルで作られる平行六面体の中には正味1個の格子点が含まれる。これは、右の赤線のセルのようにずらせば、赤い格子点のみが含まれることから容易に確認できる。したがって、
1stブリルアンゾーンの体積 ![]() = 平行六面体の体積
= 平行六面体の体積 ![]()
ベクトル解析で学ぶように、3つのベクトルで作られる平行六面体の体積はスカラー三重積で表すことができる。したがって、
![]()
である。
1stブリルアンゾーンの体積は、逆格子空間の単位胞と等しくなる。
3. まとめ
3次元でわからなくなったら、2次元に立ち返って考えると理解しやすい。
こんにちは、いつも分かりやすい図で助かっております!
ところで、六角形の逆格子点におけるブリルアンゾーンについて質問したいのですが、第一ブルリアンゾーンの面積(赤)は、オレンジ面積の1/3ではないのですか?
ご指摘ありがとうございます。
1/3ですね、すみません。格子点が3つ含まれてました。修正しました。