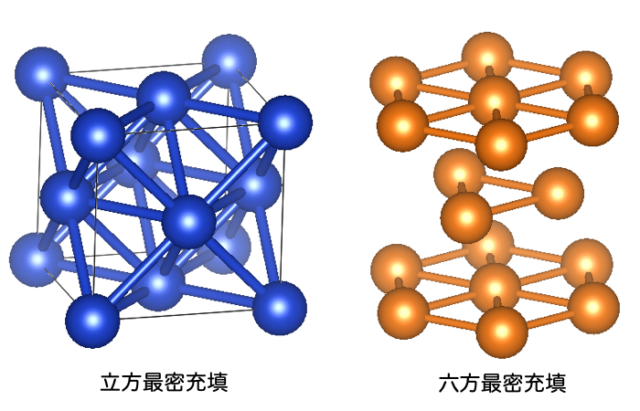
結晶構造において面心立方格子(FCC)と六方最密構造(HCP)はともに充填率が0.74で最大である。図にFCCとHCPを示す。それぞれ立方最密充填、六方最密充填と呼ばれることもある。
目次
1. 空間に球を最密に充填する
原子(球)を空間にびっしり詰めるためには、下の図のように積んでいけば良い。1段目の3つの球の上の隙間に2段目の球を置く。
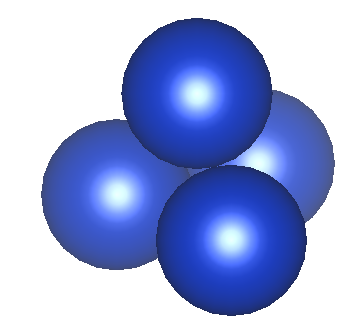
この置き方で空間を埋めていけば最密充填となる。FCCとHCPは両方ともこの置き方で充填される。したがって充填率は同じになる。
2. 面心立方格子と六方最密構造の積層
積み上げ方の違いによって生まれるFCCとHCPの違いを比べよう。
2.1 球の積み上げ
まず1段目にオレンジ球をびっしり充填する。
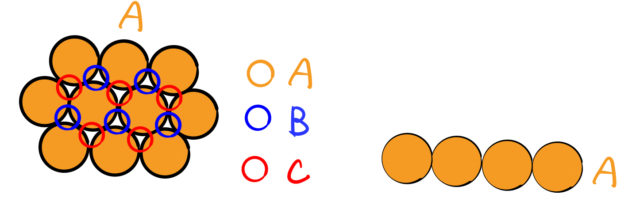
すると、最密に充填するためには
- Bに充填する
- Cに充填する
の2通りある。2段目はBの位置にブルー球を置いたとする。
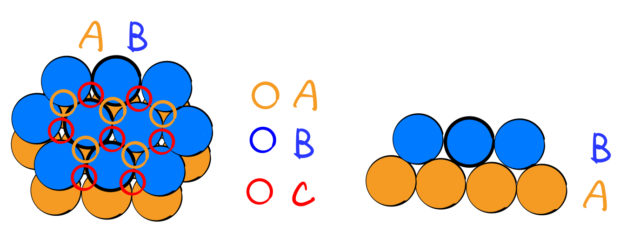
2段目のブルー球の上に3段目を積む方法は
- Aに充填する
- Cに充填する
の2通りある。どちらに詰めても最密になることは簡単にわかるだろう。Aにつめた場合とCに詰めた場合を描くと下のようになる。
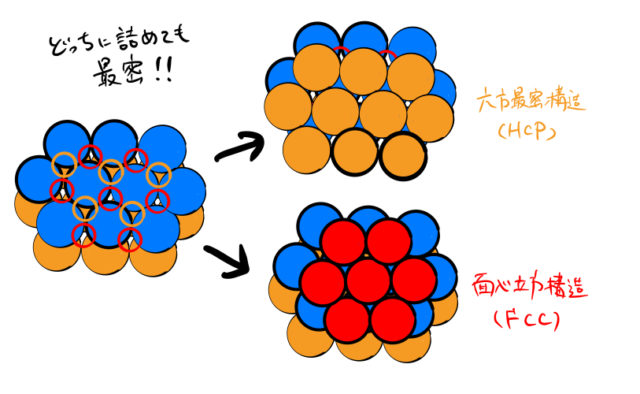
これがFCCとHCPの違いになる。つまり球を積層する場所の違いで構造の違いが生まれている。
- FCC:ABCABC…
- HCP:ABABAB…
もう一度まとめると、FCCとHCPの充填率が同じなのは、項目「1.」で説明した最密に球を詰めるルールに従っているからである。それゆえにどちらも最密構造をとる(close-packed)。また、FCCとHCPの構造の違いは積み上げ方の違いによる。
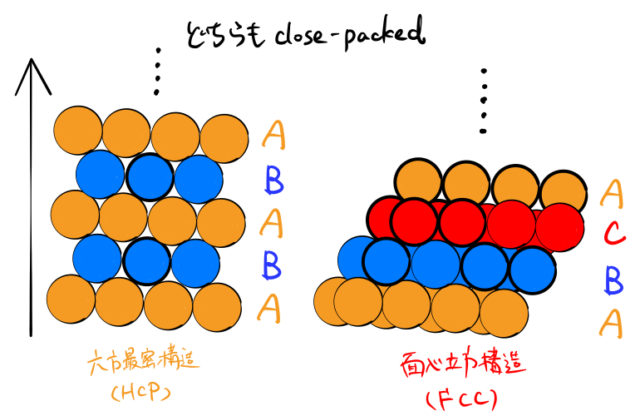
2.2 [111]方向から見たFCC
FCCとHCPが一見違うように見えるのは見る方向の問題である。FCCを[111]方向(立方体の対角線方向)から見てみると良い。
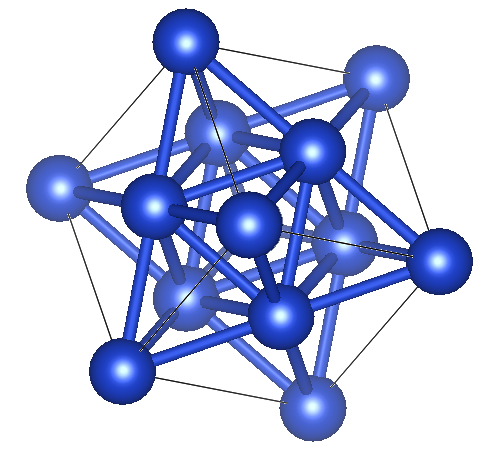
この方向から見れば六角形に見えるだろう。また、ABCABC…と層ができていることも確認できる。下のHCP(ABABAB…)との層の違いがはっきりわかる。
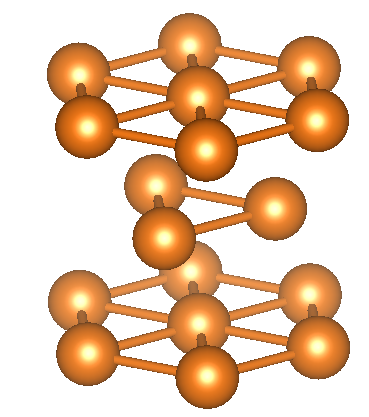
2.3 「立方最密充填」とは何か
六方最密充填構造は上で説明したHCPであった。FCCも同じ充填率をもち、最密に球を詰めることを説明した。
時折見る「立方最密充填」の意味は、空間に球を最密に詰めた立方晶系の構造のことである。したがって、「立方最密充填」は面心立方構造(FCC)のことである。六方最密充填に対応した呼び方に過ぎないので慌てないように。
3. 閃亜鉛鉱型とウルツ型(発展的)
発展的な話になる。FCC(ABCABC…)とHCP(ABABAB…)の積層と同じような関係にある結晶構造がある。それはウルツ型構造(Wurzite)と閃亜鉛鉱型(Zink Blend)である。以下でその違いをまとめた。
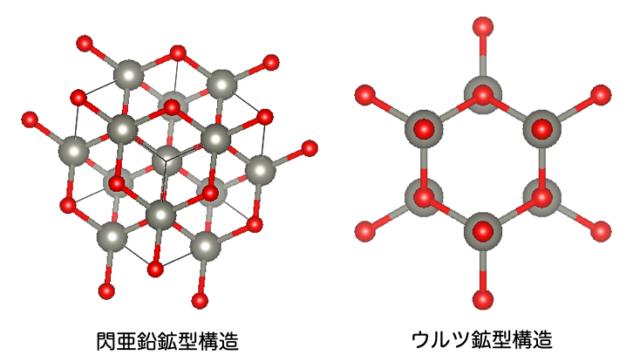
[111]方向から見た閃亜鉛鉱型構造と[001]方向から見たウルツ鉱型構造である。FCCとHCPとの違いと似ていることがわかる。
積層の違いは下のようになる。
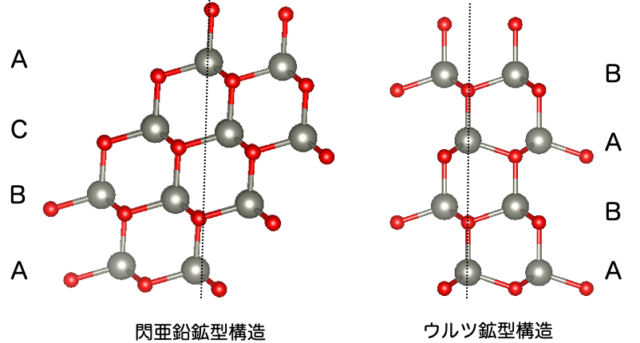
- 閃亜鉛鉱型:ABCABC…
- ウルツ鉱型:ABABAB…
ZnSなどは両方の構造をとり得ることが知られている。共有結合の話で少し触れた。
4. まとめ
FCCとHCPの簡単なまとめは下の通り。
- FCCとHCPの充填率は同じ
- FCCとHCPの原子の積み方は異なる。
- FCCは[111]方向から見よ
それぞれの結果をまとめておこう。
- FCC、閃亜鉛鉱型:ABCABC…
- HCP、ウルツ鉱型:ABABAB…