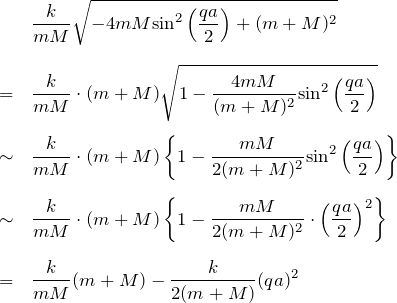以下は計算ノートも兼ねている。とくに2原子の場合は計算量が多い。1原子の場合を解説してから、2原子の場合への拡張を行う。原子同士はバネで繋がった連成振動をする。1つの粒子が相互作用なく振動するアインシュタインモデルとの違いを意識しながら学ぶと良い。参考:アインシュタインの比熱の式を導く
目次
1. 1次元鎖
格子が振動する様子を見るために、原子が1次元的にバネ(鎖)で繋がったモデルからスタートする。ここでの議論を3次元に拡張するためには、
- 波数
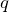
 波数ベクトル
波数ベクトル 
- 格子間隔
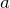
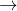 格子並進ベクトル
格子並進ベクトル 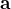
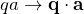
として容易に拡張できる。
2. 1原子の場合
2.1 運動方程式
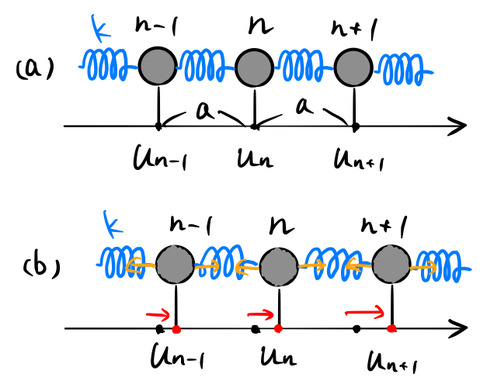
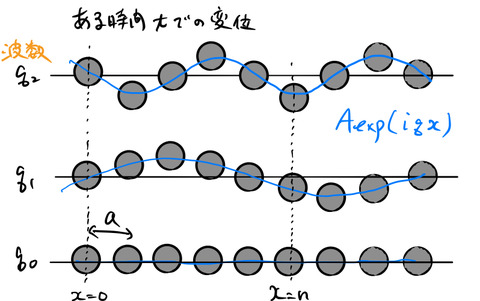
図(a)のように1次元に等間隔に格子間隔 ![]() で並んだ原子を考える。いま、この原子の位置は平衡状態にある。原子鎖におけるバネは、結晶を平衡状態に戻そうとする復元力を表している。
で並んだ原子を考える。いま、この原子の位置は平衡状態にある。原子鎖におけるバネは、結晶を平衡状態に戻そうとする復元力を表している。
問題設定は以下の通り。
- 格子間隔は
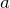
- それぞれの原子にはバネ定数
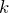 のバネがつながる
のバネがつながる 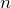 番目の原子の位置を
番目の原子の位置を 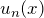 とする
とする- 図右を正の変位とする
- 原子の質量はすべて
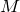 とする
とする
図(b)はそれぞれの原子が平衡位置から正の変位に動いたときの様子を表す。![]() 番目の原子に対する運動方程式をたてよう。まず原子の左右に働く復元力(図を見る)を考える。
番目の原子に対する運動方程式をたてよう。まず原子の左右に働く復元力(図を見る)を考える。
![]() 番目と
番目と ![]() 番目の原子間距離は、平衡状態(
番目の原子間距離は、平衡状態(![]() )から
)から ![]() だけ伸びている。この絵では、
だけ伸びている。この絵では、![]() は正であるが、
は正であるが、![]() が負になる(バネが縮む)ときもある。左側のバネによる復元力は右向きを正として、
が負になる(バネが縮む)ときもある。左側のバネによる復元力は右向きを正として、![]() で与えられる。
で与えられる。
右の復元力も同様に、![]() 番目と
番目と ![]() 番目の原子間距離は、平衡状態(
番目の原子間距離は、平衡状態(![]() )から
)から ![]() だけ伸びている(縮んでいる)。したがって、右側のバネによる復元力は右向きを正として、
だけ伸びている(縮んでいる)。したがって、右側のバネによる復元力は右向きを正として、![]() で与えられる。
で与えられる。
変位は右を正にとる。このとき、図(b)のように変位 ![]() として描くと符号に迷わない。つまり、
として描くと符号に迷わない。つまり、![]() 番目につながる両方のバネが伸びている絵を考える。
番目につながる両方のバネが伸びている絵を考える。
よって、![]() 番目の原子に対する運動方程式は、
番目の原子に対する運動方程式は、
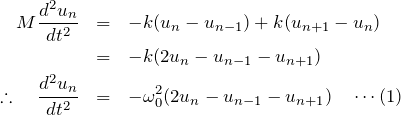
となる。ここで、
2.2 運動方程式を解く
この微分方程式の一般解は ![]() で与えられる。と個体物性の教科書にはいきなり書いてある。
で与えられる。と個体物性の教科書にはいきなり書いてある。
これは原子鎖の振動(格子振動)が波として伝わるためである。時間の項 ![]() は、
は、![]() 番目の原子の時間的な振動を表す(
番目の原子の時間的な振動を表す(![]() 番目に注目した場合)。
番目に注目した場合)。![]() は、ある時刻
は、ある時刻 ![]() で格子が波のようになっている様子を表す。図を見て欲しい(理解しやすいため横波で表している)。
で格子が波のようになっている様子を表す。図を見て欲しい(理解しやすいため横波で表している)。
ある時刻 ![]() での波の形はいろいろあると考えられる。それぞれの波は波の形を表す波長
での波の形はいろいろあると考えられる。それぞれの波は波の形を表す波長 ![]() あるいは波数
あるいは波数 ![]() で区別できる。もっとも波数が小さい(波長が長い)ものは図の
で区別できる。もっとも波数が小さい(波長が長い)ものは図の![]() である。
である。
波の式は時間 ![]() と位置
と位置 ![]() で表される。
で表される。![]() を固定して空間的な波を見るか、
を固定して空間的な波を見るか、![]() を固定して時間的な波を見るかすると理解しやすい。
を固定して時間的な波を見るかすると理解しやすい。
波数![]() で表された波は振幅を
で表された波は振幅を![]() 、位置を連続変数
、位置を連続変数 ![]() とすると、
とすると、![]() で表すことができる。図の一番左の原子を
で表すことができる。図の一番左の原子を ![]() 0番目の原子とすると、1番目の原子の位置
0番目の原子とすると、1番目の原子の位置 ![]() 、2番目の原子の位置
、2番目の原子の位置 ![]() であるため、
であるため、![]() 番目の原子位置は
番目の原子位置は ![]() となる。したがって、連続変数
となる。したがって、連続変数 ![]() に取って代わり、格子振動の場合は離散的な変数
に取って代わり、格子振動の場合は離散的な変数 ![]() によって波を表す。すなわち、空間的な波の式は
によって波を表す。すなわち、空間的な波の式は
![]()
となる。
2.3 分散関係
波数 ![]() と振動数
と振動数![]() の分散関係を求める
の分散関係を求める
では、![]() を式(1)へ代入しよう。
を式(1)へ代入しよう。![]() については下の通り。
については下の通り。
![]()
式(1)の左辺:
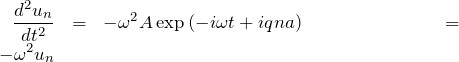
式(1)の右辺:
![Rendered by QuickLaTeX.com \begin{eqnarray*}-\omega_0^2 \{ &2&A\exp{\left( -i\omega t + iqna \right)}\\&-&A\exp{\left( -i\omega t + iqna \right)}\cdot\exp{(-iqa)}\\&-&A\exp{\left( -i\omega t + iqna \right)}\cdot\exp{( iqa)} \}\\ \\&=&-\omega_0^2 A\exp{\left( -i\omega t + iqna \right)}\left[ 2- \exp{(-iqa)} - \exp{(+iqa)}\right]\\ \\&=&-\omega_0^2 u_n\left[ 2- 2{\rm cos}(qa)\right]\quad \bigl(\because \exp(\pm iqa)={\rm cos}(qa)\pm i{\rm sin}(qa)\bigr) \\ \\&=&-4\,\omega_0^2 u_n {\rm sin}^2\left(\frac{qa}{2}\right)\quad \bigl(\because {\rm sin}^2\theta=\frac{1-{\rm cos}2\theta}{2} \bigr)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e2f8fac96163555210bd859b3da4505e_l3.png)
したがって、
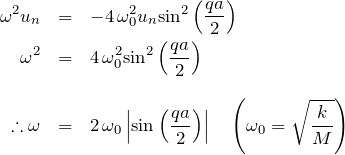
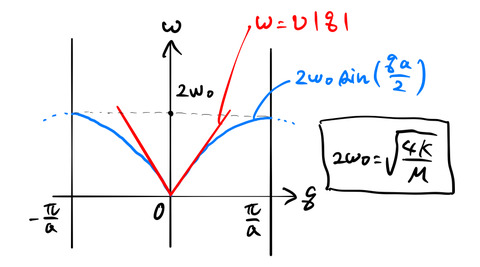
となる。この 振動数
![]() を横軸に、
を横軸に、![]() を縦軸に取り分散関係を描いてみる。
を縦軸に取り分散関係を描いてみる。![]() の周期は
の周期は ![]() である。
である。 ![]() の範囲で描くと、
の範囲で描くと、
![]() は境界(
は境界(![]() )で周期的である。また、波数
)で周期的である。また、波数 ![]() が 0 に近い領域で sin
が 0 に近い領域で sin![]() の展開を利用すると、
の展開を利用すると、
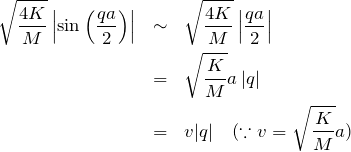
となる。したがって ![]() の小さい領域で
の小さい領域で ![]() が
が ![]() に比例する分散関係をもつ。同じく縦波である音波もこのような比例する分散関係をもつことに由来し、ここで扱った格子振動の波を
に比例する分散関係をもつ。同じく縦波である音波もこのような比例する分散関係をもつことに由来し、ここで扱った格子振動の波を
とよぶ。
3. 質量の異なる2原子の場合
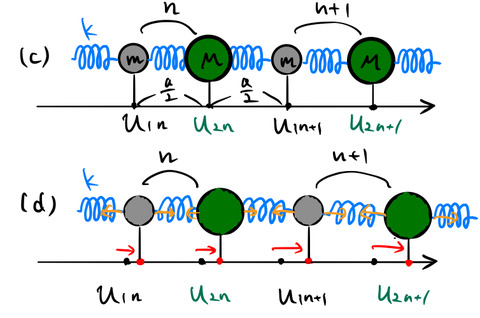
図の場合を考える。(c)は平衡位置、(d)は変位したときの図である。問題設定は、
- 格子間隔は
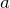
- それぞれの原子にはバネ定数
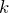 のバネがつながる
のバネがつながる 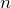 番目の原子1の位置を
番目の原子1の位置を 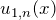 とする
とする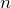 番目の原子2の位置を
番目の原子2の位置を 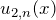 とする
とする- 図右を正の変位とする
- 原子1の質量は
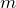 、原子2の質量は
、原子2の質量は 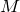 とする
とする
3.1 運動方程式
![]() に対する運動方程式は2つある。先ほどの1個の原子の場合同様に、
に対する運動方程式は2つある。先ほどの1個の原子の場合同様に、![]() 番目の原子1の左バネの伸び:
番目の原子1の左バネの伸び: ![]()
![]() 番目の原子1の右バネの伸び:
番目の原子1の右バネの伸び: ![]()
![]() 番目の原子2の左バネの伸び:
番目の原子2の左バネの伸び: ![]()
![]() 番目の原子2の右バネの伸び:
番目の原子2の右バネの伸び: ![]()
であるので、運動方程式はそれぞれ
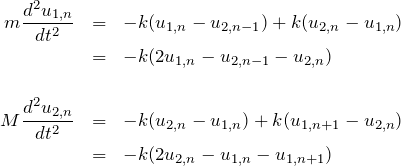
となる。
3.2 運動方程式を解く
一般解を、
![]()
として、運動方程式に代入する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&-\omega^2 m A_1 = -k(2A_1 - A_2\exp{\left( -iqa \right)} - A_2)\\ \\ \leftrightarrow &&(2k-\omega^2 m) A_1 - k[\exp{\left( -iqa \right)} +1]A_2=0 \quad\cdots (2) \\ \\ \\ &&-\omega^2 M A_2 = -k[2A_2 - A_1 - A_1\exp{\left( iqa \right)} ]\\ \\ \leftrightarrow && -k(\exp{\left( iqa \right)} +1)A_1+ ( 2k-\omega^2 M) A_2=0 \quad\cdots (3) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-dd5a374bf4847c99ae047ebca27f97d7_l3.png)
連立方程式、式(2)(3)が
![]()
この式は固有値 ![]() を求めることに対応する。得られた固有値
を求めることに対応する。得られた固有値 ![]() は
は ![]() としてエネルギーに対応する。さらに固有関数は、あとに説明する音響モード・光学モードに対応する。
としてエネルギーに対応する。さらに固有関数は、あとに説明する音響モード・光学モードに対応する。
3.3 行列式の計算
計算量があるのでコンパクトにした。
となるので、![]() に対する二次方程式の解は、
に対する二次方程式の解は、
![]()
![]() のときを考える。このとき、近似式
のときを考える。このとき、近似式
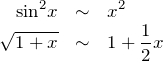
したがって式(*)より、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \omega^2 &\sim&k\left(\frac{1}{m}+\frac{1}{M}\right) \pm \left[ k\left(\frac{1}{m}+\frac{1}{M}\right) -\frac{k}{2(m+M)} \bigl( qa \bigr)^2 \right]\\ \\ &=& 2k\left( \frac{1}{m}+\frac{1}{M} \right),\; \frac{k}{2(m+M)}\bigl(qa\bigr)^2 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-d17600c220d5d0ab5c4c1ac51870b588_l3.png)
となる。一つ目の解の
3.4 光学モードと音響モード
光学モード![]() に対して
に対して
![]()
となる。原子は互いに反対方向に振動するモードとなる。イオン結晶など2種類の原子の電荷が異符号であるとき、電気双極子振動となる。したがって、光波などと相互作用するため光学モード(optical mode)と呼ばれる。
![]()
となる。この場合、2つの原子は同じ方向に振動する。1原子のときに説明したように、これは音波と同様の振動であり、音響モード(acoustic mode)と呼ばれる。
4. まとめ
計算量が多いが、丁寧に計算すれば難しいことはない。運動方程式を立てて、一般解を求められるようにしておきたい。アインシュタインの比熱の式との違いも理解しておきたい。
![Rendered by QuickLaTeX.com \begin{eqnarray*}&&(2k-\omega^2 m)(2k-\omega^2 M)-\left\{ -k\left[ \exp{(-iqa)} + 1\right] \right\}\left\{ -k\left[ \exp{( iqa)} + 1\right] \right\}\\ \\&=&mM\omega^4 - 2k(m+M)\omega^2 \\&&\quad + 4k^2-k^2 \left[ \exp{(-iqa)} + 1\right] \left[ \exp{( iqa)} + 1\right] \\ \\&=&mM\omega^4 - 2k(m+M) \omega^2 \\&&\quad + 4k^2-k^2 \left( 1+\exp{(-iqa)} +\exp{(-iqa)} + 1 \right)\\ \\&=&mM\omega^4 - 2k(m+M) \omega^2 \\&&\quad + 2k^2 - 2k^2 {\rm cos}(qa)\quad (\because \exp(\pm iqa)={\rm cos}(iqa)\pm {\rm sin}(iqa)\\ \\&=&mM\omega^4 - 2k(m+M) \omega^2 + 2k^2 [1-{\rm cos}(qa)]\\ \\&=&mM^4 - 2k(m+M) \omega^2 + 4k^2 {\rm sin}^2 \left( \frac{qa}{2} \right)\quad (\because {\rm sin}^2\theta = \frac{1-{\rm cos}\theta}{2} )\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-f3a830a1db4a1b467bc23ba7a37ac8e9_l3.png)