この記事では、振動する粒子のエネルギーを量子力学から計算し、アインシュタインの比熱の式を導く。量子論の計算手法や分配関数などの扱いに慣れるのには良い問題である。このモデルは振動を単純化しすぎている(相互作用がない)ので現実的ではない。より現実的なモデルである格子振動(連成振動)との違いも説明する。
![]()
ここで、![]() はアインシュタイン温度と呼ばれ、振動数
はアインシュタイン温度と呼ばれ、振動数 ![]() で振動する粒子のエネルギーを温度に変換したものである。 比熱の添字
で振動する粒子のエネルギーを温度に変換したものである。 比熱の添字 ![]() は定積比熱であることを意味する。つまり、熱膨張は考えていない。
は定積比熱であることを意味する。つまり、熱膨張は考えていない。
1. 予備知識
アインシュタインの比熱の式では、量子力学的な粒子の振動エネルギーを考える。また、あるエネルギーの状態を取りうる確率(相対確率)を求め、粒子の振動を統計学的に扱う必要がある。まずはじめにこれらの内容について復習しておこう。
1.1 量子力学における振動のエネルギー
量子力学では、振動数 ![]() で振動する粒子に対しては離散的な値をとる。振動する粒子が1個増えるごとに、
で振動する粒子に対しては離散的な値をとる。振動する粒子が1個増えるごとに、![]() ずつエネルギーが増えていく。したがって、
ずつエネルギーが増えていく。したがって、![]() 個の振動する粒子が存在する場合は以下の式で与えられる。
個の振動する粒子が存在する場合は以下の式で与えられる。
![]()
この式には、余分な項 ![]() がある。これは零点振動といい、粒子が振動していない場合でもエネルギーが存在していることを表す。ここでは詳細は述べないが、この零点振動は「位置と運動量が同時に決まらない不確定性原理」に由来するエネルギーである。
がある。これは零点振動といい、粒子が振動していない場合でもエネルギーが存在していることを表す。ここでは詳細は述べないが、この零点振動は「位置と運動量が同時に決まらない不確定性原理」に由来するエネルギーである。
いま、![]() は振動する粒子のエネルギーを表している。「粒子
は振動する粒子のエネルギーを表している。「粒子 ![]() 波」の関係から見れば、波を粒子として(あるいは粒子を波として)扱っている。このように振動数
波」の関係から見れば、波を粒子として(あるいは粒子を波として)扱っている。このように振動数 ![]() の波を粒子として1個, 2個と数えてエネルギーを
の波を粒子として1個, 2個と数えてエネルギーを ![]() で与えるということはいろいろな場面で出てくる。
で与えるということはいろいろな場面で出てくる。
格子振動を粒子として量子化したり、また、電荷の偏りの振動(プラズマ振動)を粒子として量子化したりするときも、![]() でエネルギーを表す。それぞれ、フォノン、プラズモンなどという。基本的に、語尾に「-on」をつけて呼称する。
でエネルギーを表す。それぞれ、フォノン、プラズモンなどという。基本的に、語尾に「-on」をつけて呼称する。
1.2 ボルツマン因子と分配関数
ボルツマン確率と分配関数は以前 詳細に説明した。詳しく知りたい方はそちらを参照していただきたい。
1.1では振動する粒子のエネルギーが ![]() で与えられることを学んだ。では、ある温度
で与えられることを学んだ。では、ある温度 ![]() でそのエネルギーを持つ粒子が存在する確率はいくらであろうか。エネルギーがわかっているときに、そのエネルギーの状態をとる相対的な確率を与える式がボルツマン因子と呼ばれるものである。
でそのエネルギーを持つ粒子が存在する確率はいくらであろうか。エネルギーがわかっているときに、そのエネルギーの状態をとる相対的な確率を与える式がボルツマン因子と呼ばれるものである。
![]()
![]() :ボルツマン定数、
:ボルツマン定数、![]() : 温度、
: 温度、![]() :振動する粒子のエネルギー
:振動する粒子のエネルギー
注意点は、ボルツマン因子は相対確率しか与えないことである。つまり、確率の総和 ![]() で、1にならない。確率の総和を1に規格化するために、
で、1にならない。確率の総和を1に規格化するために、
![]()
と 分配関数 ![]() で相対確率を割ったものを
で相対確率を割ったものを ![]() で定義する。規格化された確率は、
で定義する。規格化された確率は、 ![]() を満たす。
を満たす。![]() はボルツマン因子の総和で与えられ、状態和と呼ばれることもある。
はボルツマン因子の総和で与えられ、状態和と呼ばれることもある。
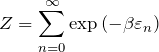
2. アインシュタインの比熱の式
比熱は温度変化に対してエネルギーがどのくらい変わるかを意味する。したがって、エネルギーを温度の関数で求める必要がある。今の振動する粒子の場合に比熱を求める手順は以下の通りである。
- 温度
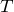 におけるエネルギーの期待値
におけるエネルギーの期待値 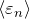 を求める
を求める 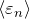 を温度
を温度 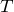 で微分する
で微分する
2.1 比熱の式を導く
いま、粒子のエネルギーとそのエネルギーを取りうる確率は以下の通りである。
![]() (1.1の内容から)
(1.1の内容から)
![]() (1.2の内容から)
(1.2の内容から)
エネルギーの期待値を計算する。
![Rendered by QuickLaTeX.com \begin{eqnarray*}\sum_n \varepsilon_n P_n&=&\frac{\sum_{n=0}^{\infty} \varepsilon_n \exp{(-\beta \varepsilon_n)}}{\sum_{m=0}^{\infty}\exp{(-\beta \varepsilon_m) }}\\ \\&=&-\frac{d}{d\beta} \left[ \ln\left( \sum_{n=0}^{\infty} \exp{(-\beta \varepsilon_n)} \right)\right]\\ \\&=&-\frac{d}{d\beta} \left\{ \ln\left[ \sum_{n=0}^{\infty} \exp{\left(-\beta \left( n+\frac{1}{2}\right)\hbar \omega_0\right)} \right]\right\} \\ \\&=&-\frac{d}{d\beta} \left\{ \ln\left[ \sum_{n=0}^{\infty} \exp{\left(-\beta n\hbar \omega_0\right) }\cdot\exp{\left(-\beta \frac{1}{2}\hbar \omega_0\right) } \right]\right\} \\ \\&=&-\frac{d}{d\beta} \left\{ \ln\left[ \exp{\left(-\beta \frac{1}{2}\hbar \omega_0\right) } \cdot \sum_{n=0}^{\infty} \exp{\left(-\beta n\hbar \omega_0\right) }\right]\right\} \\ \\&=&-\frac{d}{d\beta} \left\{ \left(-\beta \frac{1}{2}\hbar \omega_0\right)+\ln\left[ \cdot \sum_{n=0}^{\infty} \exp{\left(-\beta n\hbar \omega_0\right) }\right]\right\} \quad \cdots (1)\\&&\quad (\because \ln(ax)=\ln(a)+\ln(x))\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-aa051c3bf33e3930f9f6199b76e6bce8_l3.png)
ここで、第2項の![]() の中にある和を計算する。これは、初項 1 で 等比
の中にある和を計算する。これは、初項 1 で 等比 ![]() の無限等比級数である。したがって総和は、
の無限等比級数である。したがって総和は、
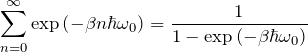
より、
![Rendered by QuickLaTeX.com \begin{eqnarray*}&&-\frac{d}{d\beta} \ln\left[\sum_{n=0}^{\infty} \exp{\left(-\beta n\hbar \omega_0\right) }\right]\\ \\ &=&-\frac{d}{d\beta} \ln\left[ \frac{1}{1-\exp{\left(-\beta \hbar \omega_0\right) } } \right]\\ \\ &=&-\frac{d}{d\beta} \left\{-\ln \left[ 1-\exp{ \left( -\beta \hbar \omega_0 \right) } \right] \right\}\\ \\ &=&\frac{\hbar\omega_0 \exp{\left(-\beta \hbar \omega_0 \right)}}{1-\exp{ \left( -\beta \hbar \omega_0 \right) }}\\ \\ &=&\frac{\hbar\omega_0}{\exp{ \left( \beta \hbar \omega_0 \right) }-1}\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-446b0a372e30b047ad4e9112f0e50352_l3.png)
また、(1)式の第1項の微分は容易に実行できる。
![]()
これらをまとめて式(1)へ代入すると、
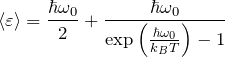
となる。これは量子論による平均エネルギーである。モル比熱を求めるために、この式へ ![]() をかけて
をかけて ![]() で微分すると、
で微分すると、
![Rendered by QuickLaTeX.com \begin{eqnarray*}3N_A\frac{d}{dT}\braket{\varepsilon}&=&3N_A\hbar \omega_0\frac{-\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2}\cdot \frac{d}{dT}\left( \frac{\hbar \omega_0}{k_B T}\right)\\ \\&=&3N_A \hbar \omega_0\frac{-\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2}\cdot \left( -\frac{\hbar \omega_0}{k_B T^2}\right)\\ \\&=&3N_A k_B\left( \frac{\hbar \omega_0}{k_B T}\right)^2\cdot\frac{\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2}\\ \\&=&3R\frac{\left( \frac{\hbar \omega_0}{k_B T}\right)^2\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2} \quad (\because R=N_A k_B)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-1d6f852bc302a9c4b0ed74dbf1f7f658_l3.png)
ここで、アインシュタイン温度
![]()
![]()
2.2 格子振動との違い
アインシュタインの比熱の式は、複数ある粒子の振動がそれぞれ独立に運動することを仮定した。したがって、振動エネルギーは単なる(粒子の個数)×![]() +(零点振動のエネルギー)であった。
+(零点振動のエネルギー)であった。
格子振動の場合は、粒子の振動は独立でない。すなわち、隣同士の原子にバネが繋がった連成振動系を考えているのである。
アインシュタインモデル:粒子の振動は独立である
格子振動:粒子の振動は独立ではない(連成振動)
3. まとめ
アインシュタインの比熱を求めるために、量子論のエネルギーを出発点として振動のエネルギーを求めた。分配関数を用いた統計的な期待値を求める計算など演習には適した問題である。
とにかく比熱を求めたいときは、
温度 ![]() でのエネルギーの期待値
でのエネルギーの期待値 ![]() を求める →
を求める → ![]() で微分する
で微分する
とすればよい。覚えておいてほしい。
深夜に申し訳ありません。
逆格子ベクトルについての記事を作成してもらえませんでしょうか?
よろしくお願いします。