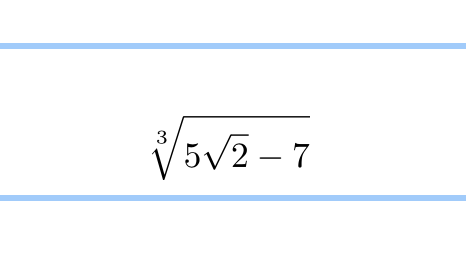過去問と実際に数学検定(数検1級)を受けた感触からまとめました。とくに1次試験の対策や勉強法として活用していただければいいと思います。「技」というより絶対に落としてはいけない問題みたいな話です。思いつき次第、随時更新していく(2019/06/18)。完全微分型を追加した(2019/09/23)。
目次
1. 大問1系
1.1 三乗根の二重根号外し
![]()
去年受けた時に1回でてたような問題です。ここで落とさないように。解き方わからない方用。
1.2 ユークリッド互除法
最大公約数を求めるのに使う。つまり、大きな数の分数を約分するときに使う。過去問で出てたので知っておいたほうがよい(参考:ユークリッド互除法の仕組み)。
2. 微分・積分/微分方程式
2.1 ウォリス積分
![]()
と定義したときに、![]() の偶奇によって積分値がすぐに求められる。
の偶奇によって積分値がすぐに求められる。
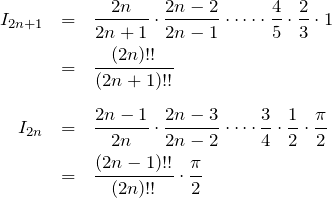
使う場面:回転体の体積(アステロイドの回転など)
2.2 全微分型の微分方程式のずるい解法
同次型の問題も完全微分型になっていれば使える。完全微分型の ![]() から直接
から直接 ![]() の
の ![]() を求めるコツみたいなことをメモしている。1次試験のときは一般解だけ書いたらよいので、これはたまに使う。
を求めるコツみたいなことをメモしている。1次試験のときは一般解だけ書いたらよいので、これはたまに使う。
3. ベクトル・行列
3.1 2ベクトルに垂直なベクトル
2つのベクトル ![]() ,
, ![]() に垂直なベクトルは外積をとればすぐにわかる。したがって、
に垂直なベクトルは外積をとればすぐにわかる。したがって、![]() は
は ![]() であり、
であり、![]() である。
である。
3.2 平行六面体・四面体の体積
外積を用いた計算で、3つのベクトルでつくられる平行六面体の体積を容易に求めることができる。それはスカラー三重積を計算して絶対値をとればよい。3つのベクトルをそれぞれ、![]() として平行六面体の体積を
として平行六面体の体積を ![]() とすれば、
とすれば、
![]()
で表すことができる。絶対値を考えるので ![]() の順番はなんでも良い。これを利用すれば、
の順番はなんでも良い。これを利用すれば、![]() から成る四面体の体積も求められる。四面体の体積
から成る四面体の体積も求められる。四面体の体積 ![]() として、
として、
![]()
となる。
3.3 空間の3ベクトルが同一平面上にある
3ベクトルが同一平面上にあるということは、平行六面体の体積が0である。つまり、スカラー3重積が0になる。
3.4 行列式で使える式
行列式の計算は ![]() の行列が、計算量的にちょうどいいのかよく出題される。とくに
の行列が、計算量的にちょうどいいのかよく出題される。とくに ![]() の行列に分けて考えるとうまくいくことがある。
の行列に分けて考えるとうまくいくことがある。![]() に分けて、
に分けて、![]() (
(![]() の零行列)の場合:
の零行列)の場合:
![]()
を使うと計算が早くなる。証明は以外に難しいので省略する。
4. 使わないもの
4.1 複素積分
複素平面は範囲であるが、複素積分はでない。留数定理も使わない。合格だけを目指すなら勉強しなくていいが、理系なら勉強しておくべき圧倒的マスト事項。
4.2 フーリエ変換・ラプラス変換
出ないけど勉強しておくべきマスト事項その2。たまに、2次試験の微分方程式を解く時に使えるかもしれない。私は過去の試験で1回使ったが、愚かにも計算ミスしていた。
5. おまけ:数検受ける人がモチベーションを上げる漫画
小学生・中学生が数学検定1級を受けるシーンがあります。老いた数学者と天才的な小学生が、数学の世界を堪能しています。現在、1巻はKindle無料で、全8巻まで出ています。