【正多面体】辺の数・面の数の覚え方

　この記事では、5つの正多面体（オイラー多面体）の点の数、面の数（と辺の数）を忘れない方法を説明する。これらの数を、自力で詰め込んで覚える必要がないということがわかるであろう。

1. オイラー多面体の双対

　すべて同じ面で構成された多面体は、「オイラー多面体」とよばれる。身近なもので言え、正四面体や正六面体（立方体）である。全部で以下の5種類存在している。

• 正四面体
• 正六面体（立方体）
• 正八面体
• 正十二面体
• 正二十面体

　これらは互いに、点と面の関係を入れ替えた「双対」の関係にある(dual corresponds)。また、このような双対の関係にあるため、「双対多面体」とも呼ばれる。

とにかく、点と面の数を覚えたい方はページの2へスキップしてください。

1.1 正六面体と正八面体

  まず双対の関係にあるものとしてわかりやすい、正六面体と正八面体についてみる。正六面体の面は6つあるので、それに対応して正八面体の点の数は6つである。また、正八面体の面の数は8つなので正六面体の点の数は6つである。

  図を見てほしい。点が面に対応しているということは、黄色で表された正八面体の6つの点を押しつぶしていくと赤色の立方体の面になることが確認できる。逆に赤色で表された正六面体の8つの点を押すと正八面体になる。非常に面白い関係である。

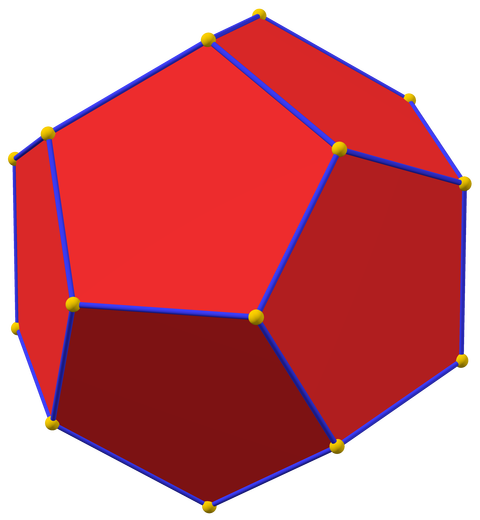
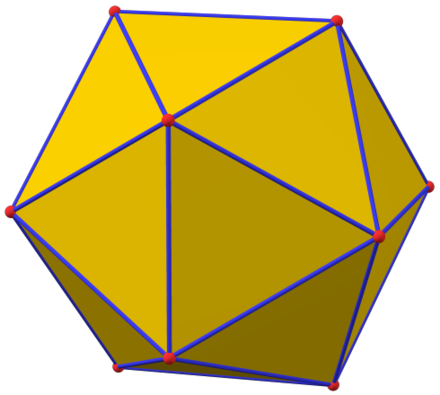
1.2 正十二面体と正二十面体

　同じように面の数が12と20のものを見てみよう。互いに面の数が点の数に対応し合うのであった。面の数が多いので想像はしにくいが、実際に点と面の数が対応することを確認できるであろう。

  2つの上図の向きはそろっているので、なんとなく点が面に対応していることが想像できよう。このように、
正六面体正八面体
の関係と同様に、
正十二面体正二十面体
の対応が見て取れる。

　では、残りの1つの正四面体の双対関係はどうなっているのであろうか。

1.3 正四面体

   正四面体の双対多面体は自分自身である。辺の数も面の数も4であり、自己双対と呼ばれる関係にある。図を見てみよう。

　たしかに、点を押していくと面になる。結局、正四面体正四面体 である。

2. 点と面の関係

ここまでの関係から以下のような点と面の数に関する表が作成できる。

	面の数	点の数
正四面体	4	4
正六面体	6	8
正八面体	8	6
正十二面体	12	20
正二十面体	20	12

   この双対関係に注目してみると、オイラー多面体の点と面の数は忘れない。辺の数は、「オイラー多面体の定理」を使うと求められる。3次元の多面体に対しては以下の関係が成り立つ。

この式を曖昧に覚えてしまうことがあるだろうが、正四面体を描いてみて辺の数、面の数、点の数を求めてみて代入してみれば良い。たしかに、6=4+4-2になっていることが確認できる。

2.1 オイラー多面体の定理を曖昧に覚えない

• どの多面体も辺の数が最も多いので、下のように符合で間違うこともない。

（辺の数）＝（面の数）ー（点の数）ー2 

• どの具体的に代入してみて正しいかチェックする。たとえば下のようにうろ覚えの式に対しては、等号が成り立たないことがわかる。

（辺の数）＝（面の数）＋（点の数）＋2 
 
基本的に公式がうろ覚えの場合は、何か簡単な具体的な数字を代入して公式がおかしくないかチェックすると良い。 

3. まとめ

　双対に注目するとスッキリ覚えられる。美しんぼ。