![]()
が完全微分型のときは
![]()
のように変形できる。 したがって、(*)から(*)’を直接求めることができれば簡単に解くことができる。 すなわち、全微分される前の形 ![]() を直接求めるのである。
を直接求めるのである。
以下の大量の例題を使って、![]() の形を作る練習をしてほしい。
の形を作る練習をしてほしい。
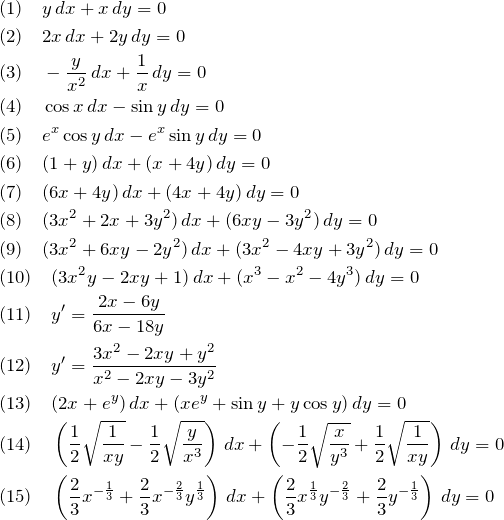
1. 完全微分型のずるい解法
ここでは例題の形からいきなり
![]()
の形をつくることを「ずるい」解法と呼ぶ(元の全微分される前の形が直接求めらるということ。)。 この方法を使っても誰かに咎められることはないと思う。
一応、「まじめな」解法と完全微分型の詳細な説明は他のところで説明した。
完全微分型であるかの見分け
完全微分型ではなかったらそもそも ![]() の形にできない。 ここでは、完全微分型の微分方程式の見分け方、すなわち左辺が
の形にできない。 ここでは、完全微分型の微分方程式の見分け方、すなわち左辺が ![]() の全微分の形になっているかどうか調べる。
の全微分の形になっているかどうか調べる。
左辺の ![]() が全微分であるための必要十分条件は
が全微分であるための必要十分条件は
![]()
が成立することである。例題のすべてでこれが成立していることは、各自確認してほしい。
自分が解けるレベルかどうか
ここで重要なのは、全微分される前の形を求めることである。
そのために必要なことは、1変数についての積分を習得しているかどうかである。 例えば
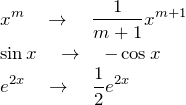
のように1変数について微分される前の形がわかるなら、もう完全微分型を解けるレベルにある。
完全微分型の場合は全微分される前の形を求めないといけない。
しかし、実際には ![]() についてそれぞれ積分する力と、以下「dfの求め方」で説明するパターンだけで対応できる。
についてそれぞれ積分する力と、以下「dfの求め方」で説明するパターンだけで対応できる。
一応、全微分なので…
全微分なので簡単な説明を加えておく。 ![]() の全微分は
の全微分は
![]()
である。これより、
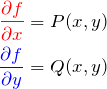
となる。
いま、例題では ![]() がそれぞれ具体的にわかっているため、上の条件より
がそれぞれ具体的にわかっているため、上の条件より ![]() を求めていく。すなわち、
を求めていく。すなわち、![]() についての積分と
についての積分と ![]() についての積分をそれぞれ実行すれば良い。
についての積分をそれぞれ実行すれば良い。
* このとき、![]() で積分する場合は
で積分する場合は ![]() を定数として計算する。
を定数として計算する。![]() で積分するときは
で積分するときは ![]() を定数扱いする。
を定数扱いする。
df(x,y)はこれだけで求められる
例題(1)(2)(6)をみて、![]() の形を求めていこう。
の形を求めていこう。
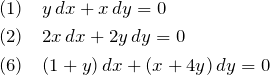
![]() に変形するために行うことは3つある。
に変形するために行うことは3つある。
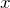 で積分する
で積分する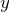 で積分する
で積分する- 積分結果から
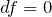 を作る
を作る
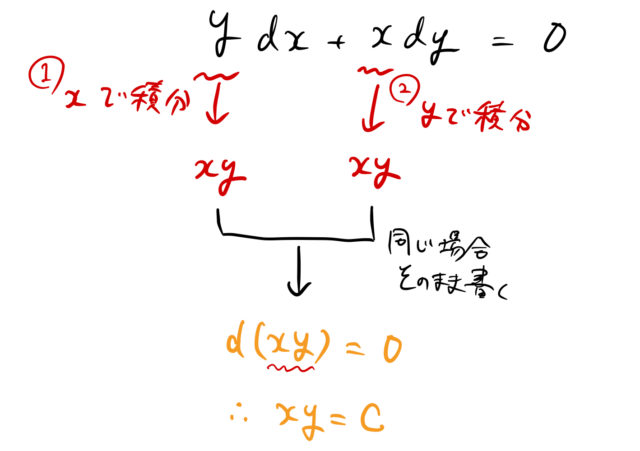
例題(1)から見ていこう。![]() のそれぞれを
のそれぞれを ![]() について積分する。 その結果、両方とも
について積分する。 その結果、両方とも ![]() になる。このとき
になる。このとき
![]()
である。つまり、全微分される前の形は ![]() である。 積分定数
である。 積分定数 ![]() を用いて、完全微分型の微分方程式の一般解が得られる。
を用いて、完全微分型の微分方程式の一般解が得られる。
![]()
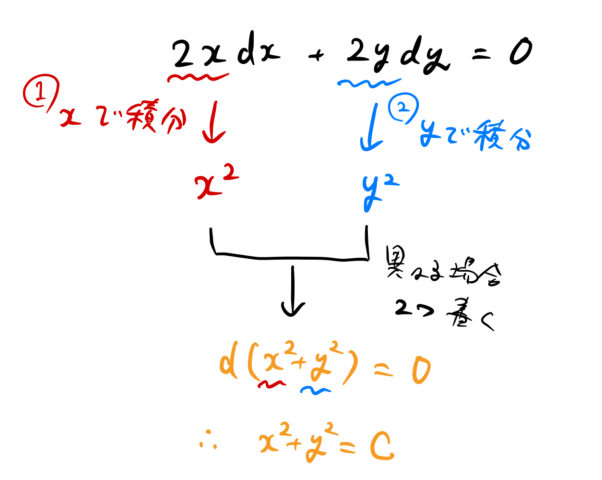
次に例題(2)を見ていく。![]() を
を ![]() で積分する。 すると
で積分する。 すると ![]() がそれぞれ得られる。2つが異なる場合は両方の和が全微分される前の
がそれぞれ得られる。2つが異なる場合は両方の和が全微分される前の ![]() になる。つまり、下のように変形できる。
になる。つまり、下のように変形できる。
![]()
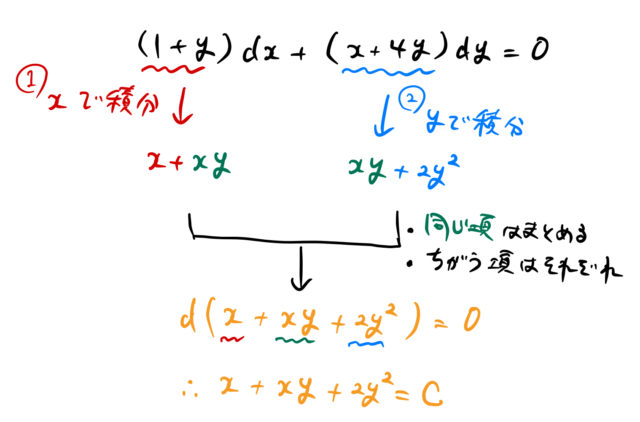
最後に例題(6)を見ていく。![]() のそれぞれに対する
のそれぞれに対する ![]() の積分は
の積分は ![]() と
と ![]() である。共通する
である。共通する ![]() はまとめてしまい、異なる項は両方使う。つまり、下のように変形できる。
はまとめてしまい、異なる項は両方使う。つまり、下のように変形できる。
![]()
完全微分型を解くためには、この3パターンだけおさえればよい。 積分が計算できるのならば、これらを組み合わせるだけで ![]() を求めることができる。
を求めることができる。
2. 例題の解答(略解)
(1)の解答
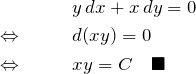
(2)の解答
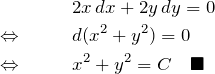
(3)の解答
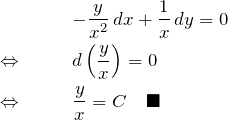
(4)の解答
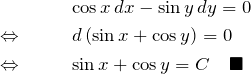
(5)の解答
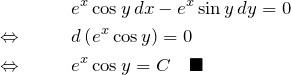
(6)の解答
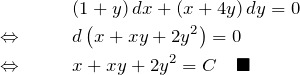
(7)の解答
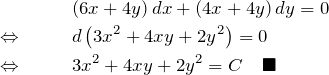
(8)の解答
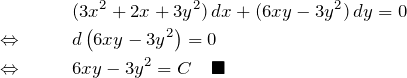
(9)の解答
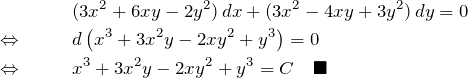
(10)の解答
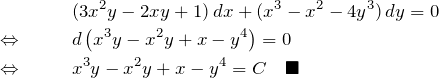
(11)の解答
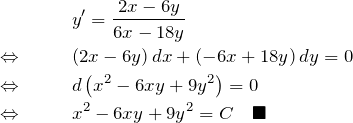
(12)の解答
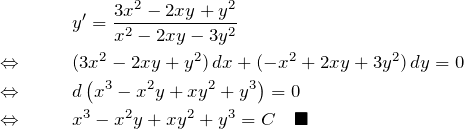
(13)の解答
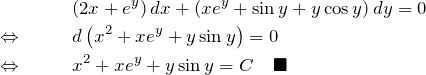
(14)の解答
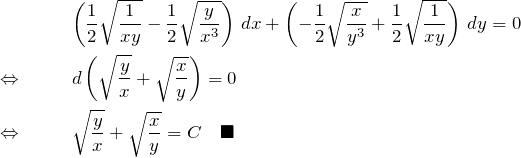
(15)の解答
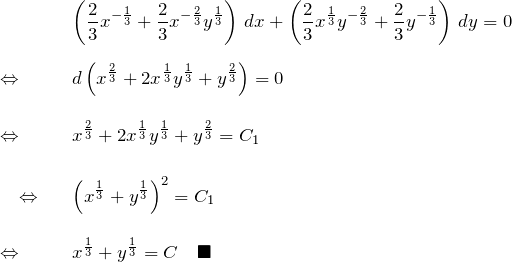
3. まとめ
かなり簡単に求めることができたと思う。また、いくつか同次型の問題が隠れていることに気づくだろう。
ここでの解法は、完全微分型の微分方程式の場合のみ有効であるということは再度確認しておきたい。完全微分型の必要十分条件は覚えているだろうか?
「こんなに楽に解けるなら、いろいろな微分方程式を完全微分型にしてしまえ」というやる気がある方は、「積分因子」について学ぶとよい。うまい積分因子があれば、完全微分型の微分方程式に帰着でき、ここで扱った解法を使うことができる。