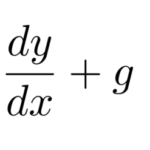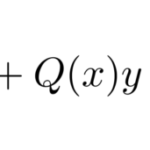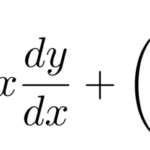全微分型の微分方程式を解く。全微分型とは
![]()
の形をしている。これは ![]() が分かれば簡単に解ける。
つまり、一般解は
が分かれば簡単に解ける。
つまり、一般解は
![]()
である。問題は「いかにして ![]() を求めるか」である。例題を解いて見ていこう。 ここでは正攻法により求める。(参考:ずるい完全微分型の解法)
を求めるか」である。例題を解いて見ていこう。 ここでは正攻法により求める。(参考:ずるい完全微分型の解法)
以下の微分方程式を解け。
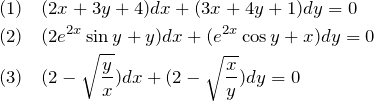
目次
1. 全微分型の微分方程式
全微分型の微分方程式の説明をおこない、その後解き方を解説する。
全微分型とは何か
全微分型が何かわからないと解き方を覚えていても仕方ないので、全微分型の形を示す。
![]()
例題を見るとわかる通り、実際は以下の形が全微分型であることを見分けないといけない。
![]()
この左辺が、何かの全微分になっていれば、(*)と一致する。すなわち、与えられた問題が全微分型であれば、
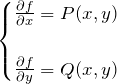
である。以下では(*)’が ![]() の全微分になるための条件を説明する。
の全微分になるための条件を説明する。
全微分型の条件
与えられた
![]()
がある関数の全微分であるための必要十分条件は
![]()
が成立することである。
初めの3つの例題の左辺
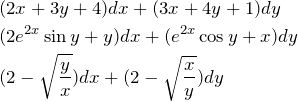
については、確かに上の必要十分条件を満たすことが確認できる。 全微分型になっているかどうかをチェックした後で、以下の解法を用いて微分方程式を解く流れである。
全微分型の解き方(簡単な例)
1変数関数 ![]() の場合
の場合
![]()
であった。したがって、2変数関数 ![]() の場合
の場合
![]()
は簡単にわかる。
いくつかの例を見ていく。
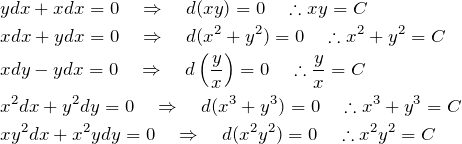
大丈夫だろうか。
結局、![]() を求めることができれば、微分方程式が解けたも同然である。
を求めることができれば、微分方程式が解けたも同然である。
f(x,y)を求める
![]()
が全微分型であることを確認した後で、![]() を求める。
を求める。 ![]() を求めるということを常に頭に置いて、下の求め方を見ていくのがよい(そうでないと迷子になる)。
を求めるということを常に頭に置いて、下の求め方を見ていくのがよい(そうでないと迷子になる)。
【![]() の求め方】
の求め方】
(*)’式の左辺が ![]() の全微分であるため、
の全微分であるため、
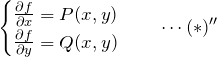
である。
上の式に対して、両辺を ![]() で積分する。
で積分する。
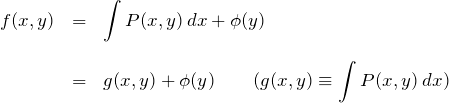
ここで、![]() は
は ![]() を含まない関数である(1変数のときの積分定数に対応)。
(*)”の下より、この
を含まない関数である(1変数のときの積分定数に対応)。
(*)”の下より、この ![]() を
を ![]() で偏微分すれば、
で偏微分すれば、![]() になる。
になる。
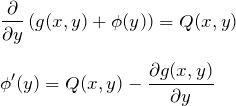
右辺の ![]() は既知であるため、両辺を
は既知であるため、両辺を ![]() で積分して
で積分して ![]() を求めることができる。
を求めることができる。
以上より、
![]()
として、![]() が求められる。したがって、微分方程式の一般解は
が求められる。したがって、微分方程式の一般解は
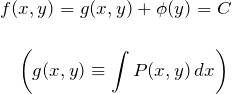
となる。
解法まとめ
全微分型微分方程式
![]()
の解き方は以下の通りである。
- 全微分型であること、以下の条件より確かめる
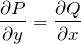
-
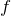 を、
を、 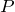 を
を 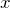 で積分した関数と
で積分した関数と 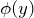 で表す
で表す 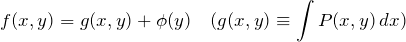
- 上の
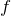 を
を 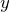 で微分したものが
で微分したものが 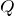 になる
になる 
- 上の式を
 で積分して、
で積分して、 を求める
を求める -
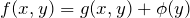 が求められ、下の式が微分方程式の一般解となる
が求められ、下の式が微分方程式の一般解となる 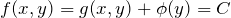
具体的に例題を解いていったほうが、圧倒的にわかりやすい。
2. 例題の解答
以下の解答で、![]() などは定数である。
などは定数である。
例題(1)の解答
![]()
について
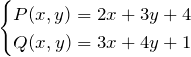
とおく。
全微分型をチェック:
![]()
より全微分型。
微分方程式の左辺が ![]() の全微分とする:
の全微分とする:
![]()
この![]() を求めたい
を求めたい
![]() から求めていく:
から求めていく:
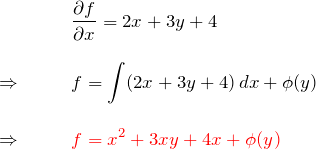
![]() を
を ![]() で偏微分したものが
で偏微分したものが ![]() :
:
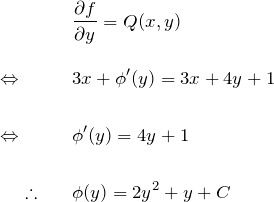
![]() がわかる:
がわかる:
![]()
一般解:
![]()
* ![]() から求めていったが、
から求めていったが、![]() から
から
![]()
を ![]() で積分して、
で積分して、![]() を求めることもできる。
を求めることもできる。
例題(2)の解答
![]()
全微分型をチェック:
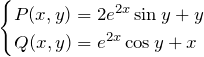
とおく。
![]()
確かに全微分であるための必要十分条件を満たす。
微分方程式の左辺が ![]() の全微分とする:
の全微分とする:
![]()
この![]() を求めたい
を求めたい
![]() から求めていく:
から求めていく:
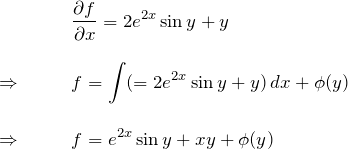
![]() を
を ![]() で偏微分したものが
で偏微分したものが ![]() :
:
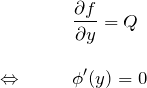
よって、
![]()
![]() がわかり、一般解がわかる:
がわかり、一般解がわかる:
![]()
例題(3)の解答
![]()
全微分型をチェック:
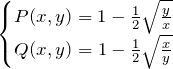
とおく。
![]()
より、確かに全微分であるための必要十分条件を満たす。
微分方程式の左辺が ![]() の全微分とする:
の全微分とする:
![]()
この![]() を求めたい
を求めたい
![]() から求めていく:
から求めていく:
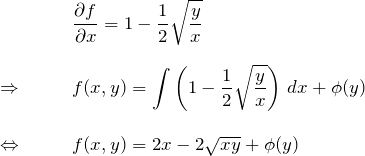
![]() を
を ![]() で偏微分したものが
で偏微分したものが ![]() :
:
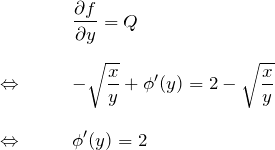
したがって、
![]()
![]() がわかり、一般解がわかる:
がわかり、一般解がわかる:
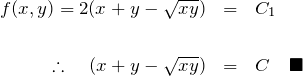
3. まとめ
全微分型の微分方程式はいかがだっただろうか。 このタイプは、具体的な例題を解いていくと自然に解き方が身につくと思う。 ただし、全微分になっているかどうかのチェックは忘れずに。